初中数学中考复习综合专题：反比例函数应用
试卷更新日期：2020-06-13 类型：一轮复习
一、综合题
-
1. 如图，一次函数y1=kx+b（k≠0）的图象与反比例函数y2= （m≠0，x<0）的图象交于点A（-3，1）和点C（-1，3），与y轴交于点B。
(1)、求一次函数与反比例函数的解析式；(2)、求△AOB的面积。2. 如图，已知A（﹣4， ），B（﹣1，m）是一次函数y＝kx+b与反比例函数 （x＜0）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D.
(1)、求一次函数解析式及m的值；(2)、P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标.3. 如图所示，在平面直角坐标系中，菱形 ABCD 的边 AD∥x 轴，直线y＝2x+b 与 x 轴交于点 B，与反比例函数 y＝ （k＞0）图象交于点 D 和点 E，OB＝3，OA＝4.
(1)、求反比例函数和一次函数的解析式；(2)、点P为线段 BE 上的一个动点，过点P作x轴的平行线，当△CDE 被这条平行线分成面积相等的两部分时，求点P的坐标.4. 在大棚中栽培新品种的蘑菇，在18℃的条件下生长最快，因此用装有恒温系统的大棚栽培，如图是某天恒温系统从开启升温到保持恒温及关闭.大棚内温度y（℃）随时间x（时）变化的函数图象，其中BC段是函数y＝ （k＞0）图像的一部分.
(1)、分别求出0≤x≤2和x≥12时对应的y与x的函数关系式；(2)、若该蘑菇适宜生长的温度不低于12℃，则这天该种蘑菇适宜生长的时间是多长？5. 如图直线y1＝﹣x+4，y2＝ x+b都与双曲线y＝ 交于点A(1，3)，这两条直线分别与x轴交于B，C两点.
(1)、求k的值；(2)、直接写出当x＞0时，不等式 x+b＞ 的解集；(3)、若点P在x轴上，连接AP，且AP把△ABC的面积分成1：2两部分，则此时点P的坐标是.6. 在平面直角坐标系中，一次函数y＝﹣x+b的图象与反比例函数y＝ (k≠0)的图象交于A、B点，与y轴交于点C，其中点A的半标为(﹣2，3)
(1)、求一次函数和反比例函数的解析式；(2)、如图，若将点C沿y轴向上平移4个单位长度至点F，连接AF、BF，求△ABF的面积.7. 如图，已知A ，B（-1，2）是一次函数 与反比例函数（ ）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D.
(1)、根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值?(2)、求一次函数解析式及m的值；(3)、P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标.8. 一辆客车从甲地出发前往乙地，平均速度v（千米/小时）与所用时间t（小时）的函数关系如图所示，其中60≤v≤120.
(1)、求出v与t的函数关系式；(2)、若一辆货车同时从乙地出发前往甲地，客车比货车平均每小时多行驶20千米，3小时后两车相遇.①求两车的平均速度；
②甲、乙两地间有两个加油站A、B，它们相距200千米，当客车进入B加油站时，货车恰好进入A加油站（两车加油的时间忽略不计），求甲地与B加油站的距离.
9. 某游泳池每次换水前后水的体积基本保持不变，当该游泳池以每小时300立方米的速度放水时，经3小时能将池内的水放完，设放水的速度为 立方米/时，将池内的水放完需 小时.已知该游泳池每小时的最大放水速度为350立方米.(1)、求 关于 的函数表达式.(2)、若该游泳池将放水速度控制在每小时200立方米至250立方米（含200立方米和250立方米），求放水时间 的范围.(3)、该游泳池能否在2.5小时内将池内的水放完？请说明理由.10. 某项工程需要砂石料 立方米，阳光公司承担了该工程运送砂石料的任务.(1)、在这项任务中平均每天的工作量V(立方米/天)与完成任务所需的时间 (天)之间具有怎样的函数关系?写出这个函数关系式.(2)、阳光公司计划投入A型卡车200辆,每天一共可以运送砂石料2x104立方米,则完成全部运送任务需多少天?(3)、如果工作了25天后,由于工程进度的需要，公司准备再投人A型卡车120辆,在保证每辆车每天工作量不变的前提下，问是否能提前28天完成任务?11. 某汽车销售商推出分期付款购车促销活动，交首付款后，余额要在30个月内结清，不计算利息，王先生在活动期间购买了价格为12万元的汽车，交了首付款后平均每月付款 万元， 个月结清. 与 的函数关系如图所示，根据图像回答下列问题：
(1)、确定 与 的函数解析式，并求出首付款的数目；(2)、王先生若用20个月结清，平均每月应付多少万元？(3)、如果打算每月付款不超过4000元，王先生至少要几个月才能结清余额？12. 某化工车间发生有害气体泄漏，自泄漏开始到完全控制利用了40min，之后将对泄漏有害气体进行清理，线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x（min）之间的函数关系（0≤x≤40），反比例函数y= 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x（min）之间的函数关系（40≤x≤？）.根据图象解答下列问题：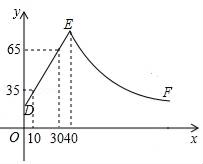
(1)、危险检测表在气体泄漏之初显示的数据是；(2)、求反比例函数y= 的表达式，并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.13. 如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于O点，训练时要求A、B两船始终关于O点对称．以O为原点，建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线y＝ 上运动，湖面风平浪静，双帆远影优美，训练中当教练船与A、B两船恰好在直线y＝x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示）．
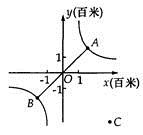(1)、发现C船时，A、B、C三船所在位置的坐标分别为A( ， )、B( ， )和C( ， )；(2)、发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到？请说明理由．14. 如图，奥运圣火抵达某市奥林匹克广场后，沿图中直角坐标系中的一段反比例函数图象传递．动点 表示火炬位置，火炬从离北京路10米处的M点开始传道，到离北京路1000米的N点时传递活动结束．迎圣火临时指挥部设在坐标原点O（北京路与奥运路的十字路口），OATB为少先队员鲜花方阵，方阵始终保持矩形形状且面积恒为10000（路线宽度均不计）．
(1)、求图中反比例函数的关系式（不需写出自变量的取值范围）；(2)、当鲜花方阵的周长为500米时，确定此时火炬的位置（用坐标表示）．15. 某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（单位：千帕）随气体体积V（单位：立方米）的变化而变化，P随V的变化情况如下表所示.P
1.5
2
2.5
3
4
…
V
64
48
38.4
32
24
…
(1)、写出符合表格数据的P关于V的函数表达式；(2)、当气球的体积为20立方米时，气球内气体的气压P为多少千帕？(3)、当气球内的气压大于144千帕时，气球将爆炸，依照（1）中的函数表达式，基于安全考虑，气球的体积至少为多少立方米？16. 为了预防“甲型H1N1”，某学校对教室采用药薰消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（mg）与时间x（min）成正比例，药物燃烧后，y与x成反比例，如图所示，现测得药物8min燃毕，此时室内空气每立方米的含药量为6mg，请你根据题中提供的信息，解答下列问题：
(1)、药物燃烧时，求y关于x的函数关系式？自变量x的取值范围是什么？药物燃烧后y与x的函数关系式呢？(2)、研究表明，当空气中每立方米的含药量低于1.6mg时，学生方可进教室，那么从消毒开始，至少需要几分钟后，学生才能进入教室？(3)、研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能杀灭空气中的毒，那么这次消毒是否有效？为什么？17. 如图，一次函数y1=ax+b的图象和反比例函数y2= 的附象相交于A(-2，3)和B(m，-1)两点。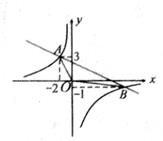
(1)、试确定一次函数与反比例函数表达式；(2)、求△OAB的面积；(3)、结合图象，直接写出使y1>y2成立的x的取值范围。18. 如图，一次函数y＝k1x+b的图象与x轴、y轴分别交于A，B两点，与反比例函数y＝ 的图象分别交于C，D两点，点C（2，4），点B是线段AC的中点.
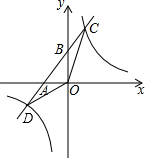(1)、求一次函数y＝k1x+b与反比例函数y＝ 的解析式；(2)、求△COD的面积；(3)、直接写出当x取什么值时，k1x+b＜ .19. 某游泳池有900立方米水，每次换水前后水的体积保持不变．设放水的平均速度为v立方米/小时，将池内的水放完需t小时，(1)、求v关于t的函数表达式，并写出自变量t的取值范围；(2)、若要求在2.5小时至3小时内（包括2.5小时与3小时）把游泳池内的水放完，求放水速度的范围．20. 已知Rt△ABC的斜边AB在平面直角坐标系的x轴上，点C（2，6）在反比例函数y1＝ 的图象上，且sin∠BAC＝(1)、求k的值和边AC的长；(2)、求点B的坐标；(3)、有一直线y2＝kx+10与y1＝ 交于M与N点，求出x为何值时，y2≥y1.21. 如图，一次函数y＝ax+b的图象与反比例函数y＝ 的图象交于C ， D两点，与x ， y轴交于B ， A两点，CE⊥x轴于点E ， 且tan∠ABO＝ ，OB＝4，OE＝1．
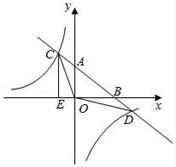(1)、求一次函数的解析式和反比例函数的解析式(2)、求△OCD的面积；(3)、根据图象直接写出一次函数的值大于反比例函数的值时，自变量x的取值范围．22. 如图，平面直角坐标系中，O为原点，点A、B分别在y轴、x轴的正半轴上．△AOB的两条外角平分线交于点P ， P在反比例函数y 的图象上．PA的延长线交x轴于点C ， PB的延长线交y轴于点D ， 连接CD ．
(1)、求∠P的度数及点P的坐标；(2)、求△OCD的面积；(3)、△AOB的面积是否存在最大值？若存在，求出最大面积；若不存在，请说明理由．23. 如图，已知直线 与 轴交于点A，与y轴交于点C，矩形ACBE的顶点B在第一象限的反比例函数 图像上，过点B作 ，垂足为F，设OF=t．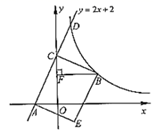
(1)、求∠ACO的正切值；(2)、求点B的坐标（用含t的式子表示）；(3)、已知直线 与反比例函数 图像都经过第一象限的点D，联结DE，如果 轴，求m的值．24. 如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y= (k>0，x>0)的图象上，点D的坐标为( ，2)。
(1)、求k的值；(2)、若将菱形ABCD沿x轴正方向平移， 当菱形的另一个顶点恰好落在函数y= (k>0，x>0)的图象上时，求菱形ABCD平移的距离。25. 如图，直线y＝kx+b与反比例函数 的图象分别交于点A（﹣1，2），点B（﹣4，n），与x轴，y轴分别交于点C ， D ．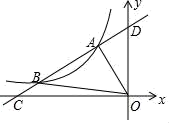
(1)、求此一次函数和反比例函数的解析式；(2)、求△AOB的面积．26. 已知关于x的一元二次方程x2﹣（2k+1）x+k2＝0有两个实数根.(1)、求k的最小整数值；(2)、设x1 ， x2是方程两根，且 ，求k的值.27. “脐橙结硕果，香飘引客来”，赣南脐橙以其“外表光洁美观，肉质脆嫩，风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售，若用2辆A型车和1辆B型车载满脐橙一次可运走10吨；用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满脐橙.根据以上信息，解答下列问题：
(1)、1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨？(2)、请你帮该物流公司设计租车方案；(3)、若1辆A型车需租金100元/次，1辆B型车需租金120元/次.请选出费用最少的租车方案，并求出最少租车费.28. 科技改变世界，随着科技的发展，自动化程度越来越高，机器人市场越来越火，某商场购进一批A，B两种品牌的编程机器人，进价分别为每台3000元、4000元，市场调查发现：销售3个A品牌机器人和2个B品牌机器人，可获利润6000元；销售2个A品牌机器人和3个B品牌机器人，可获利润6500元。(1)、此商场A，B两种品牌的编程机器人销售价格分别是多少元？(2)、若商场准备用不多于65000元的资金购进A，B两种品牌的编程机器人共20个，则至少需要购进A品牌的编程机器人多少个？(3)、不考虑其它因素，商场打算B品牌编程机器人数量不多于A品牌编程机器人数量的 ，现打算购进A，B两种品牌编程机器人共40个，怎样进货才能获得最大的利润？29. 某商场举办抽奖活动，规则如下：在不透明的袋子中有2个红球和2个黑球，这些球除颜色外都相同，顾客每次摸出1个球，若摸到红球，则获得1份奖品，若摸到黑球，则没有奖品。(1)、如果小芳只有一次摸球机会，那么小芳获得次品的概率为 ；(2)、如果小芳有两次摸球机会（摸出后不放回），求小芳获得2份奖品的概率。30. 为了保障人民群众的身体健康，在新型冠状病毒感染的肺炎疫情防控期国家有关部门加强对口罩等防疫物资的监管，严厉打击防疫物资生产领域的违法行为。在对某医药超市进行抽查时，随机抽取了5只独立包装的KN95口罩。经检测，这5只口罩中，有1只不合格品和4只合格品。(1)、从这5只口罩中随机抽取1只，抽到不合格品的概率是多少？(2)、用画树状图或列表的方法，求从这5只口罩中随机抽取2只，抽到不合格品的概率。