四川省成都市青羊区2020年中考数学二模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 2020的倒数是( )A、﹣2020 B、2020 C、 D、-2. 下面几何体中,其主视图与俯视图相同的是( )
A、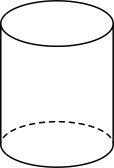
B、
B、
C、
C、
D、
D、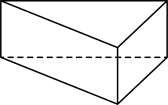
3. 习近平总书记提出了未来五年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )A、1.17×107 B、11.7×106 C、0.117×107 D、1.17×1084. 九(2)班“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别为:4,6,8,16,16。这组数据的中位数、众数分别为( )
3. 习近平总书记提出了未来五年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )A、1.17×107 B、11.7×106 C、0.117×107 D、1.17×1084. 九(2)班“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别为:4,6,8,16,16。这组数据的中位数、众数分别为( )
A、16,16 B、10,16 C、8,8 D、8,165. 如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )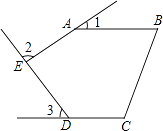 A、90° B、180° C、210° D、270°6. 在平面直角坐标系中,点(1,5)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A、90° B、180° C、210° D、270°6. 在平面直角坐标系中,点(1,5)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )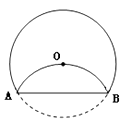 A、 B、 C、 D、8. 若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣1 B、k>﹣1且k≠0 C、k<1 D、k<1且k≠09. 在平直角坐标系中,如果抛物线y=4x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( )A、y=4(x﹣2)2+2 B、y=4(x+2)2﹣2 C、y=4(x﹣2)2﹣2 D、y=4(x+2)2+210. 一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有( )
A、 B、 C、 D、8. 若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣1 B、k>﹣1且k≠0 C、k<1 D、k<1且k≠09. 在平直角坐标系中,如果抛物线y=4x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( )A、y=4(x﹣2)2+2 B、y=4(x+2)2﹣2 C、y=4(x﹣2)2﹣2 D、y=4(x+2)2+210. 一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有( )①快车追上慢车需6小时;
②慢车比快车早出发2小时;
③快车速度为46km/h;
④慢车速度为46km/h;
⑤AB两地相距828km;
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
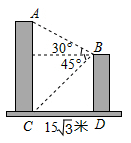
11. 分解因式:a2﹣4b2= .12. 投一枚均匀的小正方体,小正方体的每个面上分别标有数字1,2,3,4,5,6.每次实验投两次,两次朝上的数字的和为6的概率是.13. 如图,某校教学楼 与实验楼 的水平间距 米,在实验楼顶部 点测得教学楼顶部 点的仰角是 ,底部 点的俯角是 ,则教学楼 的高度是米(结果保留根号).
 14. 如图,将平行四边形 沿对角线 折叠,使点 落在点 处, ,则 的度数为.
14. 如图,将平行四边形 沿对角线 折叠,使点 落在点 处, ,则 的度数为. 15. 已知 的值为0,则 .16. 设x1 , x2是一元二次方程x2﹣x﹣1=0的两根,则2x12﹣x1+x22= .17. 如图,作半径为2的⊙O的内接正四边形ABCD,然后作正四边形ABCD的内切圆,得第二个圆,再作第二个圆的内接正四边形A1B1C1D1 , 又作正四边形A1B1C1D1的内切圆,得第三个圆…,如此下去,则第六个圆的半径为 .
15. 已知 的值为0,则 .16. 设x1 , x2是一元二次方程x2﹣x﹣1=0的两根,则2x12﹣x1+x22= .17. 如图,作半径为2的⊙O的内接正四边形ABCD,然后作正四边形ABCD的内切圆,得第二个圆,再作第二个圆的内接正四边形A1B1C1D1 , 又作正四边形A1B1C1D1的内切圆,得第三个圆…,如此下去,则第六个圆的半径为 .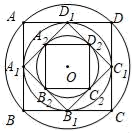 18. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2 ,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为 .
18. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2 ,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为 .
三、解答题
-
19.(1)、计算: ﹣(π﹣2020)0+2﹣1 .(2)、解不等式组: .20. 先化简,再求值: ,其中x= +1.
21. 如图,一艘船由A港沿北偏东60°方向航行20km至B港,然后再沿北偏西30°方向航行20km至C港. (1)、求A,C两港之间的距离;(结果保留到0.1km)(2)、确定C港在A港的什么方向(参考数据: ≈1.414, ≈1.732)22. 光明中学为了解九年级女同学的体育考试准备情况,随机抽取部分女同学进行了800米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图.
(1)、求A,C两港之间的距离;(结果保留到0.1km)(2)、确定C港在A港的什么方向(参考数据: ≈1.414, ≈1.732)22. 光明中学为了解九年级女同学的体育考试准备情况,随机抽取部分女同学进行了800米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图. (1)、根据给出的信息,补全两幅统计图;(2)、该校九年级有400名女生,请估计成绩未达到良好有多少名?(3)、某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会800米比赛.预赛分别为A、B、C三组进行,选手由抽签确定分组.请用列表或树状图求甲、乙两人恰好分在同一组的概率是多少?23. 如图,菱形OABC的一边OA在x轴负半轴上.O是坐标原点,点A(﹣13,0),对角线AC与OB相交于点D,且AC•OB=130,若反比例函数y= (x<0)的图象经过点D,并与BC的延长线交于点E.
(1)、根据给出的信息,补全两幅统计图;(2)、该校九年级有400名女生,请估计成绩未达到良好有多少名?(3)、某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会800米比赛.预赛分别为A、B、C三组进行,选手由抽签确定分组.请用列表或树状图求甲、乙两人恰好分在同一组的概率是多少?23. 如图,菱形OABC的一边OA在x轴负半轴上.O是坐标原点,点A(﹣13,0),对角线AC与OB相交于点D,且AC•OB=130,若反比例函数y= (x<0)的图象经过点D,并与BC的延长线交于点E. (1)、求双曲线y= 的解析式;(2)、求S△AOB:S△OCE之值.24. 如图,在⊙O中,直径AB=10,tanA= .
(1)、求双曲线y= 的解析式;(2)、求S△AOB:S△OCE之值.24. 如图,在⊙O中,直径AB=10,tanA= .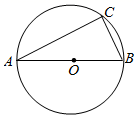 (1)、求弦AC的长;(2)、D是AB延长线上一点,且AB=kBD,连接CD,若CD与⊙O相切,求k的值;(3)、若动点P以3cm/s的速度从A点出发,沿AB方向运动,同时动点Q以 cm/s的速度从B点出发沿BC方向运动,设运动时间为t (0<t< ),连结PQ.当t为何值时,△BPQ为Rt△?25. 如图,在▱ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2 ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,求 AF长。
(1)、求弦AC的长;(2)、D是AB延长线上一点,且AB=kBD,连接CD,若CD与⊙O相切,求k的值;(3)、若动点P以3cm/s的速度从A点出发,沿AB方向运动,同时动点Q以 cm/s的速度从B点出发沿BC方向运动,设运动时间为t (0<t< ),连结PQ.当t为何值时,△BPQ为Rt△?25. 如图,在▱ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2 ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,求 AF长。 26. 某商店以固定进价一次性购进一种商品,7月份按一定售价销售,销售额为120000元,为扩大销量,减少库存,8月份在7月份售价基础上打8折销售,结果销售量增加40件,销售额增加8000元.(1)、求该商店7月份这种商品的售价是多少元?(2)、如果该商品的进价为750元,那么该商店7月份销售这种商品的利润为多少元?27. 已知四边形ABCD为矩形,对角线AC、BD相交于点O,AD=AO.点E、F为矩形边上的两个动点,且∠EOF=60°.
26. 某商店以固定进价一次性购进一种商品,7月份按一定售价销售,销售额为120000元,为扩大销量,减少库存,8月份在7月份售价基础上打8折销售,结果销售量增加40件,销售额增加8000元.(1)、求该商店7月份这种商品的售价是多少元?(2)、如果该商品的进价为750元,那么该商店7月份销售这种商品的利润为多少元?27. 已知四边形ABCD为矩形,对角线AC、BD相交于点O,AD=AO.点E、F为矩形边上的两个动点,且∠EOF=60°.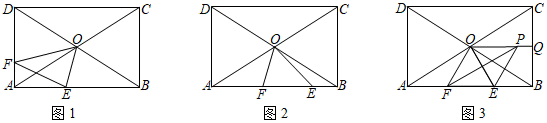 (1)、如图1,当点E、F分别位于AB、AD边上时,若∠OEB=75°,求证:DF=AE;(2)、如图2,当点E、F同时位于AB边上时,若∠OFB=75°,试说明AF与BE的数量关系;(3)、如图3,当点E、F同时在AB边上运动时,将△OEF沿OE所在直线翻折至△OEP,取线段CB的中点Q.连接PQ,若AD=2a(a>0),则当PQ最短时,求PF之长.28. 抛物线y=ax2+bx﹣5的图象与x轴交于A、B两点,与y轴交于点C,其中点A坐标为(﹣1,0),一次函数y=x+k的图象经过点B、C.
(1)、如图1,当点E、F分别位于AB、AD边上时,若∠OEB=75°,求证:DF=AE;(2)、如图2,当点E、F同时位于AB边上时,若∠OFB=75°,试说明AF与BE的数量关系;(3)、如图3,当点E、F同时在AB边上运动时,将△OEF沿OE所在直线翻折至△OEP,取线段CB的中点Q.连接PQ,若AD=2a(a>0),则当PQ最短时,求PF之长.28. 抛物线y=ax2+bx﹣5的图象与x轴交于A、B两点,与y轴交于点C,其中点A坐标为(﹣1,0),一次函数y=x+k的图象经过点B、C. (1)、试求二次函数及一次函数的解析式;(2)、如图1,点D(2,0)为x轴上一点,P为抛物线上的动点,过点P、D作直线PD交线段CB于点Q,连接PC、DC,若S△CPD=3S△CQD , 求点P的坐标;(3)、如图2,点E为抛物线位于直线BC下方图象上的一个动点,过点E作直线EG⊥x轴于点G,交直线BC于点F,当EF+ CF的值最大时,求点E的坐标.
(1)、试求二次函数及一次函数的解析式;(2)、如图1,点D(2,0)为x轴上一点,P为抛物线上的动点,过点P、D作直线PD交线段CB于点Q,连接PC、DC,若S△CPD=3S△CQD , 求点P的坐标;(3)、如图2,点E为抛物线位于直线BC下方图象上的一个动点,过点E作直线EG⊥x轴于点G,交直线BC于点F,当EF+ CF的值最大时,求点E的坐标.