四川省成都市高新区2020年中考数学二模试卷

试卷更新日期：2020-06-15 类型：中考模拟

进入出卷网下载

一、单选题

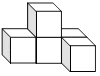
1. 下列四个实数中，比 $- 1$ 小的数是（）

A、 $- 2$ B、0 C、1 D、2

查看试题解析
2. 如图是由5个相同大小的正方体搭成的几何体，则它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 2019年10月1日上午，庆祝中华人民共和国成立70周年阅兵在北京天安门广场隆重举行，此次阅兵规模空前，这次阅兵编59个方（梯）队和联合军乐团，总规模约15000人．将数据15000用科学记数法表示为（）

A、0.15×10⁵ B、1.5×10⁴ C、15×10⁵ D、1万5千

查看试题解析
4. 下列计算正确的是（）

A、a²+a³＝a⁵ B、a²•a³＝a⁶ C、（a²）³＝a⁵ D、a⁵÷a³＝a²

查看试题解析
5. 在平面直角坐标系中，若点A（2，a）在第四象限内，则点B（a，2）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 分式方程 $\frac{3}{x - 2} - \frac{2}{x} = 0$ 的解为（）

A、x＝2 B、x＝3 C、x＝4 D、x＝﹣4

查看试题解析
7. 4月23日为世界读书日，倡导全民多读书、读好书．成都高新区某学校为了了解学生的课外阅读情况，随机抽取了一个班级的学生，对他们在今年世界读书日所在的这一周的读书时间进行了统计，统计数据如表所示：

读书时间（小时）

4

5

6

7

8

学生人数

6

10

9

8

7

则该班学生一周读书时间的中位数和众数分别是（）

A、6，5 B、6，6 C、6.5，6 D、6.5，5

查看试题解析
8. 如图，把一块含有30°角的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处，桌面的另一个顶点F与三角板斜边相交于点F，如果∠1=50°，那么∠AFE的度数为（）

A、10° B、20° C、30° D、40°

查看试题解析
9. 如图，在⊙O中，若∠CDB＝60°，⊙O的直径AB等于4，则BC的长为（）

A、 $\sqrt{3}$ B、2 C、2 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
10. 已知抛物线y＝ax²+bx+c的图象如图所示，下列说法正确的是（）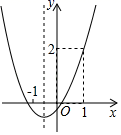

A、abc＞0 B、a﹣b+c＝2 C、4ac﹣b²＜0 D、当x＞﹣1时，y随x增大而增大

查看试题解析

二、填空题

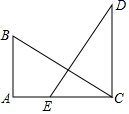
11. 4的算术平方根是， 9的平方根是， ﹣27的立方根是．

查看试题解析
12. 如图，BA⊥AC，CD∥AB，BC＝DE，且BC⊥DE，若AB＝5，CD＝8，则AE＝．

查看试题解析
13. 同一直角坐标系中，一次函数y＝k₁x+b与正比例函数y＝k₂x的图象如图所示，则满足k₁x+b＞k₂x的x取值范围是．

查看试题解析
14. 如图，在菱形ABCD中，按以下步骤作图：
①分别以点A和B为圆心，以大于 $\frac{1}{2}$ AB的长为半径作弧，两弧相交于点E、F；

②作直线EF交BC于点G，连接AG；若AG⊥BC，CG＝3，则AD的长为．

查看试题解析
15. 若实数a满足 $\sqrt{{(a - 2)}^{2}}$ ＝a﹣1，且0＜a＜ $\sqrt{3}$ ，则a＝．

查看试题解析
16. 已知x₁ ， x₂是关于x的一元二次方程x²﹣（2m﹣1）x﹣ $\frac{1}{4}$ ＝0的两个实数根，且x₁﹣x₂＝1，则m＝．

查看试题解析
17. 如图，在等边△ABC内任取一点D，连接CD，BD得到△CDB，如果等边△ABC内每一点被取到的可能性都相同，则△CBD是钝角三角形的概率是．

查看试题解析
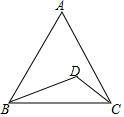18. 如图，直线l与反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象在第二象限交于B、C两点，与x轴交于点A，连接OC，∠ACO的角平分线交x轴于点D．若AB：BC：CO＝1：2：2，△COD的面积为6，则k的值为．

查看试题解析
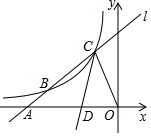19. 如图，在等腰Rt△ABC中，AC＝BC＝6 $\sqrt{2}$ ，∠EDF的顶点D是AB的中点，且∠EDF＝45°，现将∠EDF绕点D旋转一周，在旋转过程中，当∠EDF的两边DE、DF分别交直线AC于点G、H，把△DGH沿DH折叠，点G落在点M处，连接AM，若 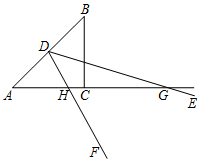$\frac{AH}{AM}$ ＝ $\frac{3}{4}$ ，则AH的长为．

查看试题解析

三、解答题

20.

(1)、计算：﹣1²+（ $\frac{1}{3}$ ）^﹣¹× $\frac{4}{\sqrt{3}}$ ﹣|1﹣2cos30°|；

(2)、解不等式组： ${\begin{array}{l} 5 x - 6 ⩽ 2 (x + 3) ① \\ \frac{x}{4} - 1 < \frac{x - 2}{3} ② \end{array}$ ．

查看试题解析
21. 先化简，再求值： $\frac{x^{2} - 1}{x^{2} - 2 x + 1}$ ÷ $\frac{x + 1}{x - 1}$ ﹣ $\frac{1 - x}{1 + x}$ ，x＝ $\sqrt{2}$ ﹣1．

查看试题解析
22. 2020年春节联欢晚会传承创新亮点多，收视率较往年大幅增长．成都高新区某学校对部分学生就2020年春晚的关注程度，采用随机抽样调査的方式，并根据收集到的信息进行统计，绘制了如图所示的两幅尚不完整的统计图（其中A表示“非常关注”；B表示“关注”；C表示“关注很少”；D表示“不关注”）．

请你根据统计图中所提供的信息解答下列问题：

(1)、直接写出m＝；估计该校1800名学生中“不关注”的人数是人；

(2)、在一次交流活动中，老师决定从本次调查回答“关注”的同学中随机选取2名同学来谈谈他们的想法，而本次调查回答“关注”的这些同学中只有一名男同学，请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率．

查看试题解析
23. 成都市天府一南站城市立交桥是成都市政府确定的城建标志性建筑，如图是立交桥引申出的部分平面图，测得拉索AB与水平桥面的夹角是37°，拉索DE与水平桥面的夹角是67°，两拉索顶端的距离AD为2m，两拉索底端距离BE为10m，请求出立柱AC的长．（参考数据tan37°≈ 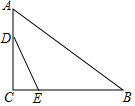$\frac{3}{4}$ ，sin37°≈ $\frac{4}{5}$ ，cos37°≈ $\frac{3}{5}$ ，tan67°≈ $\frac{12}{5}$ ，sin67°≈ $\frac{12}{13}$ ，cos67°≈ $\frac{5}{13}$ ）

查看试题解析
24. 如图，一次函数y＝x+b的图象与反比例函数y＝ $\frac{k}{x}$ （k为常数且k≠0）的图象交于A（﹣1，a）、B两点，与x轴交于点C（﹣4，0）．

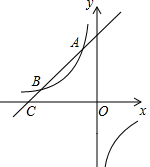(1)、求一次函数和反比例函数的表达式；

(2)、若点D是第四象限内反比例函数图象上的点，且点D到直线AC的距离为5 $\sqrt{2}$ ，求点D的横坐标．

查看试题解析
25. 如图，四边形ABCD内接于⊙O，对角线AC、BD相交于点F，AC是⊙O的直径，延长CB到点E，连接AE，∠BAE＝∠ADB，AN⊥BD，CM⊥BD，垂足分别为点N、M．

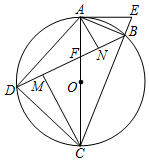(1)、证明：AE是⊙O的切线；

(2)、试探究DM与BN的数量关系并证明；

(3)、若BD＝BC，MN＝2DM，当AE＝ $\sqrt{2}$ 时，求OF的长．

查看试题解析
26. 一名大学毕业生响应国家“自主创业”的号召，在成都市高新区租用了一个门店，聘请了两名员工，计划销售一种产品．已知该产品成本价是20元/件，其销售价不低于成本价，且不高于30元/件，员工每人每天的工资为200元．经过市场调查发现，该产品每天的销售量y（件）与销售价x（元/件）之间的函数关系如图所示．

(1)、求y与x之间的函数关系式；

(2)、求每件产品销售价为多少元时，每天门店的纯利润最大？最大纯利润是多少？（纯利润＝销售收入﹣产品成本﹣员工工资）

查看试题解析
27. 将矩形ABCD沿对角线BD翻折，点A落在点A′处，AD交BC于点E，点F在CD上，连接EF，且CE＝3CF，如图1．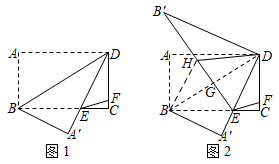

(1)、试判断△BDE的形状，并说明理由；

(2)、若∠DEF＝45°，求tan∠CDE的值；

(3)、在（2）的条件下，点G在BD上，且不与B、D两点重合，连接EG并延长到点H，使得EH＝BE，连接BH、DH，将△BDH沿DH翻折，点B的对应点B′恰好落在EH的延长线上，如图2．当BH＝8时，求GH的长．

查看试题解析
28. 如图，在平面直角坐标系xOy中，抛物线y＝ax²+bx+c的图象与x轴交于A（﹣3，0）、B（2，0）两点，与y轴交于点C（0，3）．

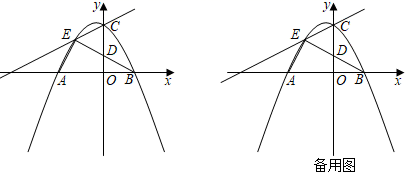(1)、求抛物线的解析式；

(2)、点E（m，2）是直线AC上方的抛物线上一点，连接EA、EB、EC，EB与y轴交于D．
①点F是x轴上一动点，连接EF，当以A、E、F为顶点的三角形与△BOD相似时，求出线段EF的长；

②点G为y轴左侧抛物线上一点，过点G作直线CE的垂线，垂足为H，若∠GCH＝∠EBA，请求出点H的坐标．

查看试题解析

读书时间（小时）	4	5	6	7	8
学生人数	6	10	9	8	7