四川省成都市成华区2020年中考数学二模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 下列关于0的说法正确的是( )A、0是正数 B、0是负数 C、0是有理数 D、0是无理数2. 一个物体如图所示,它的俯视图是( )
 A、
A、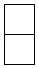 B、
B、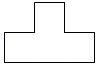 C、
C、 D、
D、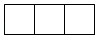 3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、平行四边形 B、矩形 C、正三角形 D、等腰直角三角形4. 截至5月6日,Covid﹣19感染人数己超365万,将365万用科学记数法表示为( )A、365×104 B、3.65×105 C、3.65×106 D、3.65×1075. 下列运算正确的是( )A、(a+3)2=a2+9 B、a8÷a2=a4 C、a2+a2=2a2 D、a2•a3=a66. 在主题为“我和我的祖国”的演讲比赛中,参加决赛的6名选手成绩(单位:分)如下:8.5,8.8,9.4,9.0,8.8,9.5,这6名选手成绩的众数和中位数分别是( )A、8.8分,8.9分 B、8.8分,8.8分 C、9.5分,8.9分 D、9.5分,8.8分7. 下列函数中,y总随x的增大而减小的是( )A、y=﹣4x B、y=x﹣4 C、y= D、y=x28. 如图, 是 的直径, ,若 ,则圆周角 的度数是( )
3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、平行四边形 B、矩形 C、正三角形 D、等腰直角三角形4. 截至5月6日,Covid﹣19感染人数己超365万,将365万用科学记数法表示为( )A、365×104 B、3.65×105 C、3.65×106 D、3.65×1075. 下列运算正确的是( )A、(a+3)2=a2+9 B、a8÷a2=a4 C、a2+a2=2a2 D、a2•a3=a66. 在主题为“我和我的祖国”的演讲比赛中,参加决赛的6名选手成绩(单位:分)如下:8.5,8.8,9.4,9.0,8.8,9.5,这6名选手成绩的众数和中位数分别是( )A、8.8分,8.9分 B、8.8分,8.8分 C、9.5分,8.9分 D、9.5分,8.8分7. 下列函数中,y总随x的增大而减小的是( )A、y=﹣4x B、y=x﹣4 C、y= D、y=x28. 如图, 是 的直径, ,若 ,则圆周角 的度数是( )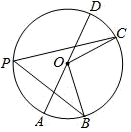 A、 B、 C、 D、9. 如图,△ABC中,∠C=90°,BC=2AC,则cosA=( )
A、 B、 C、 D、9. 如图,△ABC中,∠C=90°,BC=2AC,则cosA=( )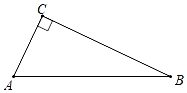 A、 B、 C、 D、10. 如图所示的抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中错误的是( )
A、 B、 C、 D、10. 如图所示的抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中错误的是( )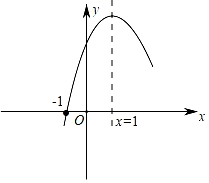 A、ac<0 B、b2﹣4ac>0 C、2a﹣b=0 D、9a+3b+c=0
A、ac<0 B、b2﹣4ac>0 C、2a﹣b=0 D、9a+3b+c=0二、填空题
-
11. 代数式 有意义,则x的取值范围是 .12. 五个大小相同的乒乓球上面分别编号为2,3,4,5,6,把它们放在不透明的袋内,从袋内任抽一个球,抽中编号是偶数的概率是 .13. 对于实数a,b,定义运算“◎”如下:a◎b=(a+b)2﹣(a﹣b)2 . 若(m+2)◎(m﹣3)=24,则m= .14. 如图,四边形ABCD中,AD∥BC,∠D=90°,AD=4,BC=3.分别以点A,C为圆心,大于 AC长为半径作弧,两弧交于点E,射线BE交AD于点F,交AC于点O.若点O恰好是AC的中点,则CD的长为 .
 15. 一元二次方程x2﹣2x﹣1=0的两根分别为x1 , x2 , 则 的值为 .16. 将等腰直角△ABC按如图方法放置在数轴上,点A和C分别对应的数是﹣2和1.以点A为圆心,AB长为半径画弧,交数轴的正半轴于点D,则点D对应的实数为 .
15. 一元二次方程x2﹣2x﹣1=0的两根分别为x1 , x2 , 则 的值为 .16. 将等腰直角△ABC按如图方法放置在数轴上,点A和C分别对应的数是﹣2和1.以点A为圆心,AB长为半径画弧,交数轴的正半轴于点D,则点D对应的实数为 .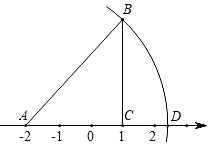 17. 从1.2.3.4四个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程ax2+4x+c=0有实数解的概率为18. 如图,点O为坐标原点,▱ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y= (x>0)的图象经过点C且S△BEF= ,则k的值为 .
17. 从1.2.3.4四个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程ax2+4x+c=0有实数解的概率为18. 如图,点O为坐标原点,▱ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y= (x>0)的图象经过点C且S△BEF= ,则k的值为 .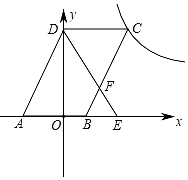 19. 如图,在矩形纸片ABCD中,AB=8,BC=6,点E是AD的中点,点F是AB上一动点.将△AEF沿直线EF折叠,点A落在点A'处.在EF上任取一点G,连接GC,GA',CA’,则△CGA'的周长的最小值为 .
19. 如图,在矩形纸片ABCD中,AB=8,BC=6,点E是AD的中点,点F是AB上一动点.将△AEF沿直线EF折叠,点A落在点A'处.在EF上任取一点G,连接GC,GA',CA’,则△CGA'的周长的最小值为 .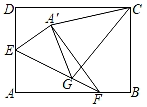
三、解答题
-
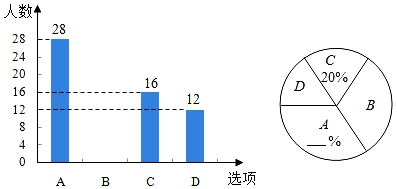
20.(1)、计算:4sin60°+(2020﹣π)0﹣( )﹣2+|﹣2 |;(2)、解不等式组: .21. 先化简,再求值: ,其中 .22. 某校在参加了成都市教育质量综合评价学业素养测试后,随机抽取八年级部分学生,针对发展水平四个维度:A﹣阅读素养、B﹣数学素养、C﹣科学素养、D﹣人文素养,开展了“你最需要提升的学业素养”问卷调查(每名学生必选且只能选择一项).现将调查的结果绘制成如图两幅不完整的统计图.
 (1)、求本次调查的学生总人数,并补全两幅统计图;(2)、求扇形统计图中的选项D对应的扇形圆心角的度数;(3)、该校八年级共有学生400人,请估计全年级选择选项B的学生有多少人?23. 如图,在A的正东方向有一港口B.某巡逻艇从A沿着北偏东55°方向巡逻,到达C时接到命令,立刻从C沿南偏东60°方向以20海里/小时的速度航行,从C到B航行了3小时.求A,B间的距离(结果保留整数).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43, ≈1.73)
(1)、求本次调查的学生总人数,并补全两幅统计图;(2)、求扇形统计图中的选项D对应的扇形圆心角的度数;(3)、该校八年级共有学生400人,请估计全年级选择选项B的学生有多少人?23. 如图,在A的正东方向有一港口B.某巡逻艇从A沿着北偏东55°方向巡逻,到达C时接到命令,立刻从C沿南偏东60°方向以20海里/小时的速度航行,从C到B航行了3小时.求A,B间的距离(结果保留整数).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43, ≈1.73) 24. 如图,一次函数y=k1x+b的图象与反比例函数y= 的图象相交于点A(﹣1,4)和点B(4,n).
24. 如图,一次函数y=k1x+b的图象与反比例函数y= 的图象相交于点A(﹣1,4)和点B(4,n).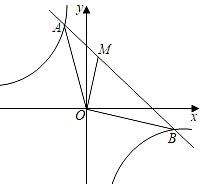 (1)、求这两个函数的解析式;(2)、已知点M在线段AB上,连接OA,OB,OM,若S△AOM= S△BOM , 求点M的坐标.25. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)、求这两个函数的解析式;(2)、已知点M在线段AB上,连接OA,OB,OM,若S△AOM= S△BOM , 求点M的坐标.25. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F. (1)、求证:直线DF是⊙O的切线;(2)、求证:BC2=4CF•AC;(3)、若⊙O的半径为2 ,∠CDF=15°,求阴影部分的面积.26. 某商场在五四青年节来临之际用2400元购进A,B两种运动衫共22件.已知购买A种运动衫与购买B种运动衫的费用相同,A种运动衫的单价是B种运动衫单价的1.2倍.(1)、求A,B两种运动衫的单价各是多少元?(2)、若计划用不超过5600元的资金再次购进A,B两种运动衫共50件,已知A,B两种运动衫的进价不变.求A种运动衫最多能购进多少件?27. 如图,已知△ABC中,AC=BC,∠ACB=120°,P为△ABC内部一点,且满足∠APB=∠BPC=150°.
(1)、求证:直线DF是⊙O的切线;(2)、求证:BC2=4CF•AC;(3)、若⊙O的半径为2 ,∠CDF=15°,求阴影部分的面积.26. 某商场在五四青年节来临之际用2400元购进A,B两种运动衫共22件.已知购买A种运动衫与购买B种运动衫的费用相同,A种运动衫的单价是B种运动衫单价的1.2倍.(1)、求A,B两种运动衫的单价各是多少元?(2)、若计划用不超过5600元的资金再次购进A,B两种运动衫共50件,已知A,B两种运动衫的进价不变.求A种运动衫最多能购进多少件?27. 如图,已知△ABC中,AC=BC,∠ACB=120°,P为△ABC内部一点,且满足∠APB=∠BPC=150°.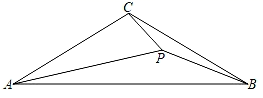 (1)、求证:△PAB∽△PBC;(2)、求证:PA=3PC;(3)、若AB=10,求PA的长.28. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(5,0),与y轴交于点C(0, ),顶点为D,对称轴交x轴于点E.
(1)、求证:△PAB∽△PBC;(2)、求证:PA=3PC;(3)、若AB=10,求PA的长.28. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(5,0),与y轴交于点C(0, ),顶点为D,对称轴交x轴于点E.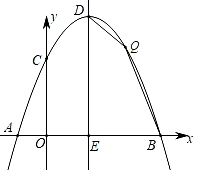 (1)、求该抛物线的一般式;(2)、若点Q为该抛物线上第一象限内一动点,且点Q在对称轴DE的右侧,求四边形DEBQ面积的最大值及此时点Q的坐标;(3)、若点P为对称轴DE上异于D,E的动点,过点D作直线PB的垂线交直线PB于点F,交x轴于点G,当△PDG为等腰三角形时,请直接写出点P的坐标.
(1)、求该抛物线的一般式;(2)、若点Q为该抛物线上第一象限内一动点,且点Q在对称轴DE的右侧,求四边形DEBQ面积的最大值及此时点Q的坐标;(3)、若点P为对称轴DE上异于D,E的动点,过点D作直线PB的垂线交直线PB于点F,交x轴于点G,当△PDG为等腰三角形时,请直接写出点P的坐标.