山西省晋中市平遥县2020年中考数学线上一模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. -2020的绝对值的倒数是( )A、 B、 C、 D、2. 窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计,下列表示我国古代窗棂样式结构图案中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、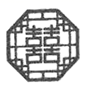 C、
C、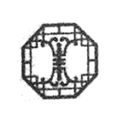 D、
D、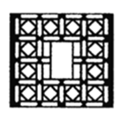 3. 如图,直线a,b被直线e,d所截,若∠1=∠2,∠3=125°,则∠4的度数为( ).
3. 如图,直线a,b被直线e,d所截,若∠1=∠2,∠3=125°,则∠4的度数为( ).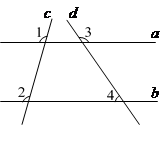 A、55° B、60° C、70° D、75°4. 关于x的一元二次方程x2+kx﹣2=0(k为实数)根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定5.
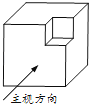
A、55° B、60° C、70° D、75°4. 关于x的一元二次方程x2+kx﹣2=0(k为实数)根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定5.从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
 A、
A、 B、
B、 C、
C、 D、
D、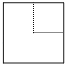 6. 研究表明,某新型冠状病毒体大小约为125纳米也就是0.125微米,而95口罩能过滤0.3微米的颗粒,并不能将病毒过滤,口罩的作用是阻挡病毒传播的“载体”,而非直接挡住病毒.1纳米就是0.000000001米.那么0.3微米用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米7. AB和DE是直立在水平地面上的两根立柱,AB=7米,某一时刻测得在阳光下的投影 米,同时,测量出 在阳光下的投影长为6米,则DE的长为( )A、 米 B、 米 C、 米 D、 米8. 如图,点 的坐标是 ,点 的坐标是 , 为 的中点,将 绕点 逆时针旋转 后得到 ,若反比例函数 的图象恰好经过 的中点 ,则 的值是( )
6. 研究表明,某新型冠状病毒体大小约为125纳米也就是0.125微米,而95口罩能过滤0.3微米的颗粒,并不能将病毒过滤,口罩的作用是阻挡病毒传播的“载体”,而非直接挡住病毒.1纳米就是0.000000001米.那么0.3微米用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米7. AB和DE是直立在水平地面上的两根立柱,AB=7米,某一时刻测得在阳光下的投影 米,同时,测量出 在阳光下的投影长为6米,则DE的长为( )A、 米 B、 米 C、 米 D、 米8. 如图,点 的坐标是 ,点 的坐标是 , 为 的中点,将 绕点 逆时针旋转 后得到 ,若反比例函数 的图象恰好经过 的中点 ,则 的值是( )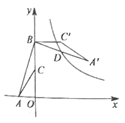 A、24 B、25 C、26 D、309. 如图, ,以点 为圆心,以任意长为半径作弧交 , 于 , 两点;分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;以 为端点作射线 ,在射线 上截取线段 ,则射线 上与点 的距离为 的点有( )
A、24 B、25 C、26 D、309. 如图, ,以点 为圆心,以任意长为半径作弧交 , 于 , 两点;分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;以 为端点作射线 ,在射线 上截取线段 ,则射线 上与点 的距离为 的点有( )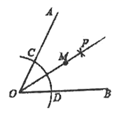 A、1个 B、2个 C、3个 D、0个10. 如图, 中, , , ,阴影部分的面积是( )
A、1个 B、2个 C、3个 D、0个10. 如图, 中, , , ,阴影部分的面积是( )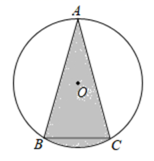 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 方程 的解为 .12. 在平面直角坐标系,点 坐标 ,点 坐标..,点 是线段 的中点,若以原点 为位似中心,把线段 缩小为原来的 得到线段 ,则点 的对应点 坐标是 .13. 如图,四边形ABCD内接于 ,若四边形ABCO是平行四边形,则 的大小为 .
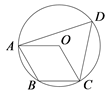 14. 如图,一架长为 米的梯子 斜靠在一竖直的墙 上,这时测得 ,如果梯子的底端 外移到 ,则梯子顶端 下移到 ,这时又测得 ,那么 的长度约为米.( , , , )
14. 如图,一架长为 米的梯子 斜靠在一竖直的墙 上,这时测得 ,如果梯子的底端 外移到 ,则梯子顶端 下移到 ,这时又测得 ,那么 的长度约为米.( , , , )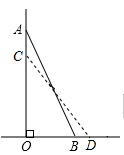 15. 如图,将一张矩形纸片ABCD沿对角线BD折叠,点C的对应点为 ,再将所折得的图形沿EF折叠,使得点D和点A重合 若 , ,则折痕EF的长为 .
15. 如图,将一张矩形纸片ABCD沿对角线BD折叠,点C的对应点为 ,再将所折得的图形沿EF折叠,使得点D和点A重合 若 , ,则折痕EF的长为 .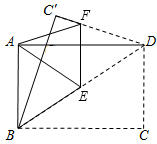
三、解答题
-
16.(1)、 ;(2)、解方程:
① ;
② .
17. 如图,已知菱形中 ,且 延长 至点 ,使 ,连接 和 .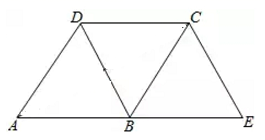 (1)、求证: ;(2)、求证:四边形 是菱形.18. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 , 两点,与 轴交于点 .
(1)、求证: ;(2)、求证:四边形 是菱形.18. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 , 两点,与 轴交于点 . (1)、请直接写出不等式 的解集;(2)、将 轴下方的图象沿 轴翻折,点 落在点 处,连接 , ,求 的面积.19. “一方有难,八方支援”是中华民族的传统美德.2月20日13时25分,山西第12批支援武汉医疗队整装出发,在抗击新冠病毒战役中,我省支援湖北医疗队共1500多人奔赴武汉.其中小丽、小王和三个同事共五人直接派往一线某医院,根据该医院人事安排需要先抽出一人去急诊科,再派两人到发热门诊,请你利用所学知识完成下列问题.
(1)、请直接写出不等式 的解集;(2)、将 轴下方的图象沿 轴翻折,点 落在点 处,连接 , ,求 的面积.19. “一方有难,八方支援”是中华民族的传统美德.2月20日13时25分,山西第12批支援武汉医疗队整装出发,在抗击新冠病毒战役中,我省支援湖北医疗队共1500多人奔赴武汉.其中小丽、小王和三个同事共五人直接派往一线某医院,根据该医院人事安排需要先抽出一人去急诊科,再派两人到发热门诊,请你利用所学知识完成下列问题. (1)、小丽被派往急诊科的概率是;(2)、若正好抽出她们一同事去往急诊科,请你利用画树状图或列表的方法,求出小丽和小王同时被派往发热门诊的概率.20. 为确保贫困人口到2020年底如期脱贫,习总书记提出扶贫开发“贵在精准,重在精准,成败之举在于精准”,近年来扶贫工作小组对果农进行精准扶贫,帮助果农因地制宜种植一种有机生态水果并拓宽了市场,有机生态水果产量呈逐年上升,去年这种水果的产量是亩产约1000千克.(1)、预计明年这种水果产量要达到亩产1440千克,求这种水果亩产量去年到明年平均每年的增长率为多少?(2)、某水果店从果农处直接以每千克24元批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克,若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为 元,当每千克的平均销售价为多少元时.该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计)21. 在探究锐角三角函数的意义的学习过程中,小亮发现:“如图1,在 中, ,可探究得到 ”
(1)、小丽被派往急诊科的概率是;(2)、若正好抽出她们一同事去往急诊科,请你利用画树状图或列表的方法,求出小丽和小王同时被派往发热门诊的概率.20. 为确保贫困人口到2020年底如期脱贫,习总书记提出扶贫开发“贵在精准,重在精准,成败之举在于精准”,近年来扶贫工作小组对果农进行精准扶贫,帮助果农因地制宜种植一种有机生态水果并拓宽了市场,有机生态水果产量呈逐年上升,去年这种水果的产量是亩产约1000千克.(1)、预计明年这种水果产量要达到亩产1440千克,求这种水果亩产量去年到明年平均每年的增长率为多少?(2)、某水果店从果农处直接以每千克24元批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克,若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为 元,当每千克的平均销售价为多少元时.该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计)21. 在探究锐角三角函数的意义的学习过程中,小亮发现:“如图1,在 中, ,可探究得到 ”
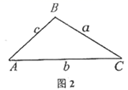 (1)、请你利用图1探究说明小亮的说法是否正确;(2)、小丽猜想“如果在钝角三角形中,两个锐角正弦值与它们所对边的边长之间也有一定的关系“在图2的钝角 中, 是钝角,请你利用图2帮小丽探究 与 之间的关系,并写出探究过程.(3)、在锐角 中, , , 之间存在什么关系,请你探究并直接写出结论.22. 阅读材料:
(1)、请你利用图1探究说明小亮的说法是否正确;(2)、小丽猜想“如果在钝角三角形中,两个锐角正弦值与它们所对边的边长之间也有一定的关系“在图2的钝角 中, 是钝角,请你利用图2帮小丽探究 与 之间的关系,并写出探究过程.(3)、在锐角 中, , , 之间存在什么关系,请你探究并直接写出结论.22. 阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在 中, , ,分别过 、 向经过点 直线作垂线,垂足分别为 、 ,我们很容易发现结论: .
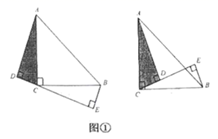 (1)、探究问题:如果 ,其他条件不变,如图②,可得到结论;
(1)、探究问题:如果 ,其他条件不变,如图②,可得到结论;.请你说明理由.
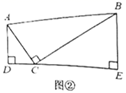 (2)、学以致用:如图③,在平面直角坐标系中,直线 与直线 交于点 ,且两直线夹角为 ,且 ,请你求出直线 的解析式.
(2)、学以致用:如图③,在平面直角坐标系中,直线 与直线 交于点 ,且两直线夹角为 ,且 ,请你求出直线 的解析式.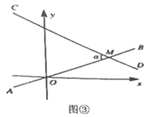 (3)、拓展应用:如图④,在矩形 中, , ,点 为 边上—个动点,连接 ,将线段 绕点 顺时针旋转 ,点 落在点 处,当点 在矩形 外部时,连接 , .若 为直角三角形时,请你探究并直接写出 的长.
(3)、拓展应用:如图④,在矩形 中, , ,点 为 边上—个动点,连接 ,将线段 绕点 顺时针旋转 ,点 落在点 处,当点 在矩形 外部时,连接 , .若 为直角三角形时,请你探究并直接写出 的长.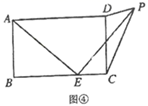 23. 如图,已知抛物线 经过 , ,对称轴为直线 .
23. 如图,已知抛物线 经过 , ,对称轴为直线 . (1)、求该抛物线和直线 的解析式;(2)、点 是直线 上方抛物线上的动点,设 点的横坐标为 ,试用含 的代数式表示 的面积,并求出 面积的最大值;(3)、设P点是直线 上一动点, 为抛物线上的点,是否存在点 ,使以点 、 、P、 为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点 坐标,不存在说明理由.
(1)、求该抛物线和直线 的解析式;(2)、点 是直线 上方抛物线上的动点,设 点的横坐标为 ,试用含 的代数式表示 的面积,并求出 面积的最大值;(3)、设P点是直线 上一动点, 为抛物线上的点,是否存在点 ,使以点 、 、P、 为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点 坐标,不存在说明理由.