山东省日照市五莲县2020年中考数学一模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 的平方根是( )A、± B、± C、 D、2. 下列四种图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列因式分解正确的是( )A、 B、 C、 D、4. 若关于 的不等式组 恰有两个整数解,求实数a的取值范围是( )A、 B、 C、 D、5. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x2)=196 B、50+50(1+x2)=196 C、50+50(1+x)+50(1+x)2=196 D、50+50(1+x)+50(1+2x)=1966. 在同一坐标系内,一次函数 与二次函数 y=ax2+8x+b 的图象可能是 ( )A、
3. 下列因式分解正确的是( )A、 B、 C、 D、4. 若关于 的不等式组 恰有两个整数解,求实数a的取值范围是( )A、 B、 C、 D、5. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x2)=196 B、50+50(1+x2)=196 C、50+50(1+x)+50(1+x)2=196 D、50+50(1+x)+50(1+2x)=1966. 在同一坐标系内,一次函数 与二次函数 y=ax2+8x+b 的图象可能是 ( )A、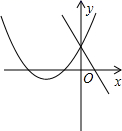 B、
B、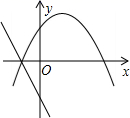 C、
C、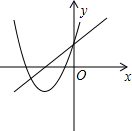 D、
D、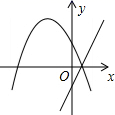 7. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
7. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )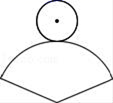 A、r B、2 r C、 r D、3r8. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 ,那么点B′的坐标是( )
A、r B、2 r C、 r D、3r8. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 ,那么点B′的坐标是( )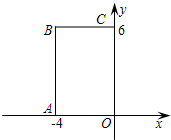 A、(-2,3) B、(2,-3) C、(3,-2)或(-2,3) D、(-2,3)或(2,-3)9. 如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
A、(-2,3) B、(2,-3) C、(3,-2)或(-2,3) D、(-2,3)或(2,-3)9. 如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
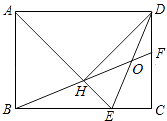 A、2个 B、3个 C、4个 D、5个10. 方程 有两个实数根,则m的取值范围( )A、 B、 且 C、 D、 且11. 如图,正方形 的边长为 ,动点 从点 出发以 的速度沿着边 运动,到达点 停止运动,另一动点 同时从点 出发,以 的速度沿着边 向点 运动,到达点 停止运动,设点 运动时间为 , 的面积为 ,则 关于 的函数图象是( )
A、2个 B、3个 C、4个 D、5个10. 方程 有两个实数根,则m的取值范围( )A、 B、 且 C、 D、 且11. 如图,正方形 的边长为 ,动点 从点 出发以 的速度沿着边 运动,到达点 停止运动,另一动点 同时从点 出发,以 的速度沿着边 向点 运动,到达点 停止运动,设点 运动时间为 , 的面积为 ,则 关于 的函数图象是( ) A、
A、 B、
B、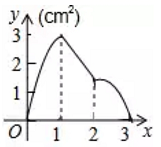 C、
C、 D、
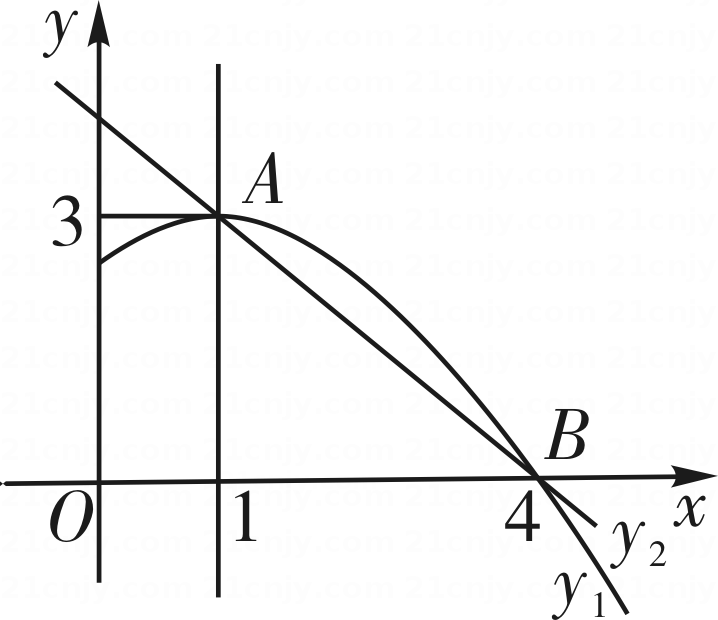
D、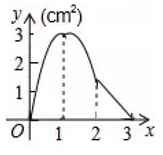 12. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
12. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是( )
 A、①②③ B、①③④ C、①③⑤ D、②④⑤
A、①②③ B、①③④ C、①③⑤ D、②④⑤二、填空题
-
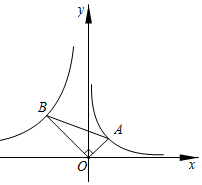
13. 已知 , 是方程 的两个根,则 .14. 当直线 经过第二、三、四象限时,则 的取值范围是 .15. 如图, 中, ,顶点 , 分别在反比例函数 与 的图象上,则 的值为 .
 16. 如图,直线 与抛物线 交于 , 两点,点 是 轴上的一个动点,当 的周长最小时, .
16. 如图,直线 与抛物线 交于 , 两点,点 是 轴上的一个动点,当 的周长最小时, .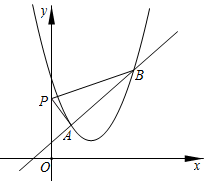
三、解答题
-
17.(1)、计算: .(2)、先化简,再求值: ,其中, .18. 为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
整理情况
频数
频率
非常好
0.21
较好
70
0.35
一般
m
不好
36
请根据图表中提供的信息,解答下列问题:
(1)、本次抽样共调查了名学生;(2)、m=;(3)、该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?(4)、某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.19. 浩然文具店新到一种计算器,进价为25元,营销时发现:当销售单价定为30元时,每天的销售量为150件,若销售单价每上涨1元,每天的销售量就会减少10件.(1)、写出商店销售这种计算器,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价定为多少元时,每天的销售利润最大?最大值是多少?(3)、商店的营销部结合上述情况,提出了A、B两种营销方案:方案A:为了让利学生,该计算器的销售利润不超过进价的24%;
方案B:为了满足市场需要,每天的销售量不少于120件.
请比较哪种方案的最大利润更高,并说明理由.
20. 如图,在 中, , 的平分线 交 于点 ,点 在 上,以 为直径的 经过点 . (1)、求证:① 是 的切线;
(1)、求证:① 是 的切线;② ;
(2)、若点 是劣弧 的中点,且 ,试求阴影部分的面积.21. 已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d= 计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d= = = = .
根据以上材料,解答下列问题:
(1)、求点P(1,﹣1)到直线y=x﹣1的距离;(2)、已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y= x+9的位置关系并说明理由;(3)、已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.22. 如图,已知抛物线y=ax2+bx+c过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.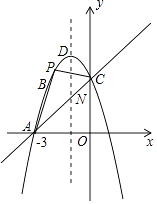 (1)、求抛物线的解析式;(2)、设点M(1,m),当MB+MD的值最小时,求m的值;(3)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;(4)、若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.
(1)、求抛物线的解析式;(2)、设点M(1,m),当MB+MD的值最小时,求m的值;(3)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;(4)、若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.