山东省济南市市中区2020年中考数学一模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
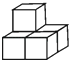 A、
A、 B、
B、 C、
C、 D、
D、 3. 2019年1月3日,“嫦娥四号”探测器成功着陆在月球背面东经177.6度、南纬45.5度附近,实现了人类首次在月球背面软着陆.数字177.6用科学记数法表示为( )A、0.1776×103 B、1.776×102 C、1.776×103 D、17.76×1024. 如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( )
3. 2019年1月3日,“嫦娥四号”探测器成功着陆在月球背面东经177.6度、南纬45.5度附近,实现了人类首次在月球背面软着陆.数字177.6用科学记数法表示为( )A、0.1776×103 B、1.776×102 C、1.776×103 D、17.76×1024. 如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( ) A、60° B、50° C、45° D、40°5. 为调查某校1500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有( )
A、60° B、50° C、45° D、40°5. 为调查某校1500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有( ) A、1200名 B、450名 C、400名 D、300名6. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
A、1200名 B、450名 C、400名 D、300名6. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、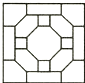 B、
B、 C、
C、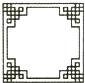 D、
D、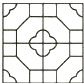 7. 如图,已知双曲线 上有一点 ,过 作 垂直 轴于点 ,连接 ,则 的面积为( )
7. 如图,已知双曲线 上有一点 ,过 作 垂直 轴于点 ,连接 ,则 的面积为( ) A、 B、 C、 D、8. 化简 + 的结果是( )A、x﹣2 B、 C、 D、9. 如图将 绕点 逆时针旋转 得到相应的 若点 恰在线段 的延长线上,则下列选项中错误的是( )
A、 B、 C、 D、8. 化简 + 的结果是( )A、x﹣2 B、 C、 D、9. 如图将 绕点 逆时针旋转 得到相应的 若点 恰在线段 的延长线上,则下列选项中错误的是( ) A、 B、 C、 D、10. 已知关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是( )A、k>且k≠2 B、k≥且k≠2 C、k >且k≠2 D、k≥且k≠211. 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角45°的传送带AB,调整为坡度i=1: 的新传送带AC(如图所示).已知原传送带AB的长是4 米,那么新传送带AC的长是( )
A、 B、 C、 D、10. 已知关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是( )A、k>且k≠2 B、k≥且k≠2 C、k >且k≠2 D、k≥且k≠211. 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角45°的传送带AB,调整为坡度i=1: 的新传送带AC(如图所示).已知原传送带AB的长是4 米,那么新传送带AC的长是( )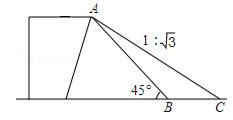 A、8米 B、4米 C、6米 D、3米12. 如图,在△ABC中,∠ACB=90°,AB=10,tanA= .点P是斜边AB上一个动点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
A、8米 B、4米 C、6米 D、3米12. 如图,在△ABC中,∠ACB=90°,AB=10,tanA= .点P是斜边AB上一个动点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 分解因式:2a2+4a+2= .14. 如图,添加一个条件: , 使△ADE∽△ACB,(写出一个即可)
 15. 某中学足球队的18名队员的年龄情况如下表:
15. 某中学足球队的18名队员的年龄情况如下表:年龄(岁)
14
15
16
17
18
人数
3
6
4
4
1
则这些队员年龄的众数和中位数分别是 .
16. 如图,已知菱形ABCD的面积为6cm2 , BD的长为4cm,则AC的长为cm. 17. 将抛物线y=x2向左平移2个单位,再向下平移5个单位,则平移后所得新抛物线的表达式为 .18. 在平面直角坐标系中,已知 、 ,B为y轴上的动点,以AB为边构造 ,使点C在x轴上, 为BC的中点,则PM的最小值为.
17. 将抛物线y=x2向左平移2个单位,再向下平移5个单位,则平移后所得新抛物线的表达式为 .18. 在平面直角坐标系中,已知 、 ,B为y轴上的动点,以AB为边构造 ,使点C在x轴上, 为BC的中点,则PM的最小值为.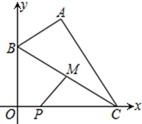
三、解答题
-
19. 计算: +|-4|-2cos30°.20. 解不等式组 ,并写出它的所有整数解.21. 如图,点A,F,C,D在同一直线上,点B与点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC,求证:BC=EF.
 22. 某小区响应济南市提出的“建绿透绿”号召,购买了银杏树和玉兰树共150棵用来美化小区环境,购买银杏树用了12000元,购买玉兰树用了9000元.已知玉兰树的单价是银杏树单价的1.5倍,那么银杏树和玉兰树的单价各是多少?
22. 某小区响应济南市提出的“建绿透绿”号召,购买了银杏树和玉兰树共150棵用来美化小区环境,购买银杏树用了12000元,购买玉兰树用了9000元.已知玉兰树的单价是银杏树单价的1.5倍,那么银杏树和玉兰树的单价各是多少?
23. 小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题: (1)、小帅的骑车速度为千米/小时;点C的坐标为;(2)、求线段AB对应的函数表达式;(3)、当小帅到达乙地时,小泽距乙地还有多远?24. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的
(1)、小帅的骑车速度为千米/小时;点C的坐标为;(2)、求线段AB对应的函数表达式;(3)、当小帅到达乙地时,小泽距乙地还有多远?24. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:  (1)、这次调查的学生共有多少名;(2)、请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数;(3)、如果要在这
(1)、这次调查的学生共有多少名;(2)、请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数;(3)、如果要在这 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E). 25. 如图,在平面直角坐标系中,直线 经过点 和 ,双曲线 经过点B.
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E). 25. 如图,在平面直角坐标系中,直线 经过点 和 ,双曲线 经过点B. (1)、求直线 和双曲线 的函数表达式;(2)、点C从点A出发,沿过点A与y轴平行的直线向下运动,速度为每秒1个单位长度,点C的运动时间为t(0<t<12),连接BC,作BD⊥BC交x轴于点D,连接CD,
(1)、求直线 和双曲线 的函数表达式;(2)、点C从点A出发,沿过点A与y轴平行的直线向下运动,速度为每秒1个单位长度,点C的运动时间为t(0<t<12),连接BC,作BD⊥BC交x轴于点D,连接CD,①当点C在双曲线上时,求t的值;
②在0<t<6范围内,∠BCD的大小如果发生变化,求tan∠BCD的变化范围;如果不发生变化,求tan∠BCD的值;
③当 时,请求出t的值.
26. 如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,顶点C在y轴上,OA=8,OC=4.点P为对角线AC 上一动点,过点P作PQ⊥PB,PQ交x轴于点Q. (1)、tan∠ACB=;(2)、在点P从点C运动到点A的过程中, 的值是否发生变化?如果变化,请求出其变化范围;如果不变,请求出其值;(3)、若将△QAB沿直线BQ折叠后,点A与点P重合,则PC的长为27. 如图,在平面直角坐标系中,抛物线y=ax2+bx+4经过A(﹣3,0)、B(4,0)两点,且与y轴交于点C,D(4﹣4 ,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
(1)、tan∠ACB=;(2)、在点P从点C运动到点A的过程中, 的值是否发生变化?如果变化,请求出其变化范围;如果不变,请求出其值;(3)、若将△QAB沿直线BQ折叠后,点A与点P重合,则PC的长为27. 如图,在平面直角坐标系中,抛物线y=ax2+bx+4经过A(﹣3,0)、B(4,0)两点,且与y轴交于点C,D(4﹣4 ,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.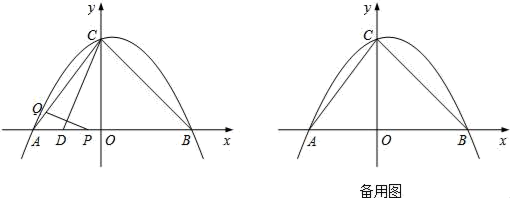 (1)、求该抛物线的解析式;(2)、若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;(3)、在第一象限的抛物线上取一点G,使得S△GCB=S△GCA , 再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
(1)、求该抛物线的解析式;(2)、若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;(3)、在第一象限的抛物线上取一点G,使得S△GCB=S△GCA , 再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.