山东省济南市历下区2020年中考数学二模试卷

试卷更新日期：2020-06-15 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的倒数是（）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 在下面的四个几何体中，左视图与主视图不相同的几何体是（）

A、 B、 C、 D、

查看试题解析
3. 2020年初，新型冠状病毒来势汹汹，迅速在全球蔓延开来，严重危及人们的生命安全，“90后”成为这场战“疫”的主力军，为中国抗击疫情作出了卓越的贡献！据报道，新型冠状病毒的直径约0.0000001米，这个数用科学记数法表示为（）

A、 $1 \times 10^{7}$ B、 $0.1 \times 10^{- 6}$ C、 $1 \times 10^{- 7}$ D、 $10 \times 10^{- 8}$

查看试题解析
4. 如图，AB//CD，∠A=50°，则∠1的度数是（）

A、40° B、50° C、130° D、150°

查看试题解析
5. 下面计算正确的是（）

A、6a－5a＝1 B、a＋2a²＝3a² C、－（a－b）＝－a＋b D、2（a＋b）＝2a＋b

查看试题解析
6. 下列图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 在平面直角坐标系中，与点 $(- 2, 3)$ 关于y轴对称的点的坐标为（）

A、 $(- 3, 2)$ B、 $(- 2, - 3)$ C、 $(3, - 2)$ D、 $(2, 3)$

查看试题解析
8. 一个口袋中有 3 个黑球和若干个白球，在不允许将球倒出来数的前提下，小明为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色，…，不断重复上述过程．小明共摸了100次，其中25次摸到黑球．根据上述数据，小明可估计口袋中的白球大约有（）

A、12 个 B、15 个 C、9 个 D、10 个

查看试题解析
9. 如图， $Δ A B C$ 内接于 $⊙ O$ ，若 $∠ A = 45^{°}$ ， $⊙ O$ 的半径 $r = 4$ ，则阴影部分的面积为（）

A、 $4 π - 8$ B、 $2 π$ C、 $4 π$ D、 $8 π - 8$

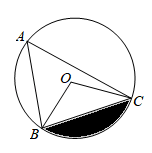查看试题解析
10. 如图，AB ， AC分别是⊙O的直径和弦， $O D ⊥ A C$ 于点D ，连接BD ， BC ，且 $A B = 10$ ， $A C = 8$ ，则BD的长为（）

A、 $2 \sqrt{5}$ B、4 C、 $2 \sqrt{13}$ D、4.8

查看试题解析
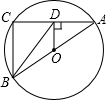11.
如图，将矩形ABCD绕点A旋转至矩形AB′C′D′位置，此时AC的中点恰好与D点重合，AB交CD于点E．若AB=6，则△AEC的面积为（　　）

A、12 B、4 $\sqrt{3}$ C、8 $\sqrt{3}$ D、6

查看试题解析
12. 如果我们把函数 $y = a x^{2} + b | x | + c$ 称为二次函数 $y = a x^{2} + b x + c$ 的“镜子函数”，那么对于二次函数 $C_{1}$ ： $y = x^{2} - 2 x - 3$ 的“镜子函数” $C_{2}$ ： $y = x^{2} - 2 | x | - 3$ ，下列说法：① $C_{2}$ 的图像关于y轴对称；② $C_{2}$ 有最小值，最小值为 $- 4$ ；③当方程 $x^{2} - 2 | x | - 3 = m$ 有两个不相等的实数根时， $m > - 3$ ；④直线 $y = x + b$ 与 $C_{2}$ 的图像有三个交点时， $- \frac{13}{4} \leq b \leq - 3$ 中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 分解因式： $3 x^{2} - 12 =$ ．

查看试题解析
14. 正方形的边长为6，则该正方形的边心距是．

查看试题解析
15. 有一组数据如下：2，3，3，4，则这组数据的方差是．

查看试题解析
16. 如图，一游人由山脚A沿坡角为30°的山坡AB行走600m，到达一个景点B，再由B沿山坡BC行走200m到达山顶C，若在山顶C处观测到景点B的俯角为45°，则山高CD=（结果用根号表示）．

查看试题解析
17. 如图，直线 $l ⊥ x$ 轴于点 $P$ ，且与反比例函数 $y_{1} = \frac{k_{1}}{x}$ （ $x > 0$ ）及 $y_{2} = \frac{k_{2}}{x}$ （ $x > 0$ ）的图象分别交于 $A$ 、 $B$ 两点，连接 $O A$ 、 $O B$ ，已知 $Δ O A B$ 的面积为4，则 $k_{1} ﹣ k_{2} =$ ．

查看试题解析
18. 如图，矩形 $A B C D$ 中，点E在 $A D$ 上，过点E作 $E F ⊥ B E$ 交 $C D$ 于F，且 $B C = B E = 10$ ， $F C = F E = 5$ ，点M是线段 $C F$ 上的动点，连接 $B M$ ，过点E作 $B M$ 的垂线交 $B C$ 于点N，垂足为H．以下结论：① $∠ F E D = ∠ E B A$ ；② $A E = 6$ ；③ $\frac{E N}{B M} = \frac{A B}{A D}$ ；④连接 $C H$ ，则 $C H$ 的最小值为 $5 \sqrt{3} - 5$ ；其中正确的结论是（所有正确结论的序号都填上）．

查看试题解析

三、解答题

19. $\sqrt{8} + {(\frac{1}{2})}^{- 2} - 4 \sin 45 ° + 2020^{0}$ ．

查看试题解析
20. 解不等式组： ${\begin{array}{l} 5 x - 2 > 3 (x - 1) \\ \frac{x}{2} \geq \frac{2 x - 1}{3} \end{array}$ ，并写出它的所有整数解．

查看试题解析
21. 如图，四边形ABCD是正方形，M为BC上一点，连接AM，延长AD至点E，使得AE=AM，过点E作EF⊥AM，垂足为F，求证：AB=EF．

查看试题解析
22. 某汽车专卖店销售A、B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，两种车型的销售总额为96万元；本周销售2辆A型车和1辆B型车，两种车型的销售总额为62万元，已知两种型号汽车销售价格始终不变．

(1)、求A、B两种车型的销售单价分别是多少？

(2)、第三周计划售出A、B两种型号的车共5辆，若销售总额不少于100万元，则B型车至少要售出多少辆？

查看试题解析
23. 如图，PA与⊙O相切于点A，过点A作AB⊥OP，垂足为C，交⊙O于点B.连接PB，AO，并延长AO交⊙O于点D，与PB的延长线交于点E.

(1)、求证：PB是⊙O的切线；

(2)、若OC=3，AC=4，求PB的长.

查看试题解析
24. 随着通讯技术的迅猛发展，人与人之间的沟通方式变得更多样、便捷．某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种），在全校范围内随机调查了部分学生，将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息回答下列问题：

(1)、本次调查共调查了名学生；在扇形统计图中，表示“QQ”的扇形圆心角的度数为；

(2)、将条形统计图补充完整；

(3)、该校共有1500名学生，请估计该校最喜欢用“微信”沟通的学生有多少名？

(4)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系，请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率．

查看试题解析
25. 菱形 $A B C D$ 的顶点C与原点O重合，点B落在y轴正半轴上，点A、D落在第一象限内，且D点坐标为 $(4 ， 3)$ ．

(1)、如图1，若反比例函数 $y = \frac{k}{x}$ （ $x > 0$ ）的图象经过点A，求k的值；

(2)、菱形 $A B C D$ 向右平移t个单位得到菱形 $A_{1} B_{1} C_{1} D_{1}$ ，如图2．
①请写出点 $B_{1}$ 、 $D_{1}$ 的坐标（用合1的代数式表示）.

②是否存在反比例函数 $y = \frac{n}{x}$ （ $x > 0$ ），使得点 $B_{1}$ 、 $D_{1}$ 同时落在 $y = \frac{n}{x}$ （ $x > 0$ ）的图象上？若存在，求n的值；若不存在，请说明理由．

查看试题解析
26. 如图， $B C$ 为等边 $△ A B M$ 的高， $A B = 4$ ，点P为直线 $B C$ 上的动点（不与点B重合），连接 $A P$ ，将线段 $A P$ 绕点P逆时针旋转60°，得到线段 $P D$ ，连接 $M D$ 、 $B D$ ．

(1)、问题发现：如图①，当点D在直线 $B C$ 上时，线段 $B P$ 与 $M D$ 的数量关系为， $∠ D M B =$ ；

(2)、拓展探究：如图②，当点P在 $B C$ 的延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；

(3)、问题解决：当 $∠ B D M = 30 °$ 时，请直接写出线段 $A P$ 的长度．

查看试题解析
27. 如图1，抛物线 $y = x^{2} + b x + c$ 与x轴交于A、B两点，与y轴交于C点，连接 $A C$ 、 $B C$ ，已知点A、C的坐标为 $A (- 2 ， 0)$ 、 $C (0 ， - 6)$ ．

(1)、求抛物线的表达式；

(2)、点P是线段 $B C$ 下方抛物线上的一动点，如果在x轴上存在点Q，使得以点B、C、P、Q为顶点的四边形为平行四边形，求点Q的坐标；

(3)、如图2，若点M是 $△ A O C$ 内一动点，且满足 $A M = A O$ ，过点M作 $M N ⊥ O A$ ，垂足为N，设 $△ A M N$ 的内心为I，试求 $C I$ 的最小值．

查看试题解析