内蒙古呼和浩特市玉泉区2020年中考数学模拟试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 据国家统计局2018年1月18日公布,2017年我国GDP总量为827122亿元,首次登上80万亿元的门槛,数据827122亿元用科学记数法表示为( )A、8.27122×1012 B、8.27122×1013 C、0.827122×1014 D、8.27122×10142. 如图是由5个相同的正方体搭成的几何体,其左视图是( )
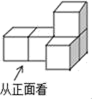 A、
A、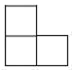 B、
B、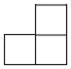 C、
C、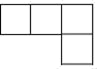 D、
D、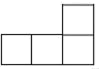 3. 已知关于x的不等式 的解集如图所示,则a的值是
3. 已知关于x的不等式 的解集如图所示,则a的值是 A、 B、 C、 D、04. 已知x+ =6,则x2+ =( )A、38 B、36 C、34 D、325.
A、 B、 C、 D、04. 已知x+ =6,则x2+ =( )A、38 B、36 C、34 D、325.抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
 A、20,20 B、30,20 C、30,30 D、20,306. 方程 有两个实数根,则k的取值范围是( ).A、k≥1 B、k≤1 C、k>1 D、k<17. 如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A、20,20 B、30,20 C、30,30 D、20,306. 方程 有两个实数根,则k的取值范围是( ).A、k≥1 B、k≤1 C、k>1 D、k<17. 如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )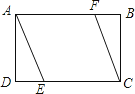 A、 B、 C、1 D、8. 将三粒均匀的分别标有 , , , , , 的正六面体骰子同时掷出,朝上一面上的数字分别为 , , ,则 , , 正好是直角三角形三边长的概率是( )A、 B、 C、 D、9. 已知圆锥的底面半径为5cm,侧面积为60πcm2 , 设圆锥的母线与高的夹角为θ,则sinθ的值为( )
A、 B、 C、1 D、8. 将三粒均匀的分别标有 , , , , , 的正六面体骰子同时掷出,朝上一面上的数字分别为 , , ,则 , , 正好是直角三角形三边长的概率是( )A、 B、 C、 D、9. 已知圆锥的底面半径为5cm,侧面积为60πcm2 , 设圆锥的母线与高的夹角为θ,则sinθ的值为( ) A、 B、 C、 D、10. 如图,点A,B为反比例函数y= 在第一象限上的两点,AC⊥y轴于点C,BD⊥x轴于点D,若B点的横坐标是A点横坐标的一半,且图中阴影部分的面积为k﹣2,则k的值为( )
A、 B、 C、 D、10. 如图,点A,B为反比例函数y= 在第一象限上的两点,AC⊥y轴于点C,BD⊥x轴于点D,若B点的横坐标是A点横坐标的一半,且图中阴影部分的面积为k﹣2,则k的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:x3y﹣2x2y+xy= .12. a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是bc(用“>”或“<”号填空)13. m是方程2x2+3x﹣1=0的根,则式子4m2+6m+2018的值为.14. 如图,在四边形 中, , 且 与 不平行, , ,对角线 平分 , , 分别是底边 , 的中点,连接 ,点 是 上的任意一点,连接 , ,则 的最小值为 .
 15. 如图,在 中, , , ,将 绕点 顺时针旋转 后得到 ,将线段 绕点 逆时针旋转 后得到线段 ,分別以 、 为圆心, 、 长为半径画弧 和弧 ,连接 ,则图中阴影部分的面积是 .
15. 如图,在 中, , , ,将 绕点 顺时针旋转 后得到 ,将线段 绕点 逆时针旋转 后得到线段 ,分別以 、 为圆心, 、 长为半径画弧 和弧 ,连接 ,则图中阴影部分的面积是 . 16. 如图,在 中, , , ,点 是 的中点,点 在边 上,将 沿 翻折,使点 落在点 处,当 时, .
16. 如图,在 中, , , ,点 是 的中点,点 在边 上,将 沿 翻折,使点 落在点 处,当 时, .
三、解答题
-
17.(1)、计算 .(2)、先化简,再求, ,其中 .18. 关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1 , x2.(1)、求m的取值范围.(2)、若2(x1+x2)+x1x2+10=0.求m的值.19. 如图,已知A、F、C、D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.
 (1)、求证:△ABC≌△DEF;
(1)、求证:△ABC≌△DEF;
(2)、若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.20. 如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH= 米,HF= 米,HE=1米. (1)、求篮板底部支架HE与支架AF所成的∠FHE的度数.(2)、求篮板底部点E到地面的距离,(精确到0.01米)(参考数据: ≈1.41, ≈1.73)21. 在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).(1)、请你用画树状图或列表的方法,写出点M所有可能的坐标;(2)、求点M(x,y)在函数y=﹣ 的图象上的概率.22. 2013年我国多地出现雾霾天气,某企业抓住商机准备生产空气净化设备,该企业决定从以下两个投资方案中选择一个进行投资生产,方案一:生产甲产品,每件产品成本为a元(a为常数,且40<a<100),每件产品销售价为120元,每年最多可生产125万件;方案二:生产乙产品,每件产品成本价为80元,每件产品销售价为180元,每年可生产120万件,另外,年销售x万件乙产品时需上交0.5x2万元的特别关税,在不考虑其它因素的情况下:(1)、分别写出该企业两个投资方案的年利润y1(万元)、y2(万元)与相应生产件数x(万件)(x为正整数)之间的函数关系式,并指出自变量的取值范围;(2)、分别求出这两个投资方案的最大年利润;(3)、如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?23. 反比例函数y= (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)、求篮板底部支架HE与支架AF所成的∠FHE的度数.(2)、求篮板底部点E到地面的距离,(精确到0.01米)(参考数据: ≈1.41, ≈1.73)21. 在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).(1)、请你用画树状图或列表的方法,写出点M所有可能的坐标;(2)、求点M(x,y)在函数y=﹣ 的图象上的概率.22. 2013年我国多地出现雾霾天气,某企业抓住商机准备生产空气净化设备,该企业决定从以下两个投资方案中选择一个进行投资生产,方案一:生产甲产品,每件产品成本为a元(a为常数,且40<a<100),每件产品销售价为120元,每年最多可生产125万件;方案二:生产乙产品,每件产品成本价为80元,每件产品销售价为180元,每年可生产120万件,另外,年销售x万件乙产品时需上交0.5x2万元的特别关税,在不考虑其它因素的情况下:(1)、分别写出该企业两个投资方案的年利润y1(万元)、y2(万元)与相应生产件数x(万件)(x为正整数)之间的函数关系式,并指出自变量的取值范围;(2)、分别求出这两个投资方案的最大年利润;(3)、如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?23. 反比例函数y= (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).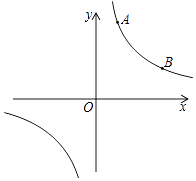 (1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.24. 如图,已知 是△ 的外角 的平分线,交 的延长线于点 ,延长 交△ 的外接圆于点 ,连接 , .
(1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.24. 如图,已知 是△ 的外角 的平分线,交 的延长线于点 ,延长 交△ 的外接圆于点 ,连接 , . (1)、求证: .(2)、已知 ,若 是△ 外接圆的直径, ,求 的长.25. 如图,抛物线 与直线 分别相交于 , 两点,且此抛物线与 轴的一个交点为 ,连接 , .已知 , .
(1)、求证: .(2)、已知 ,若 是△ 外接圆的直径, ,求 的长.25. 如图,抛物线 与直线 分别相交于 , 两点,且此抛物线与 轴的一个交点为 ,连接 , .已知 , . (1)、求抛物线的解析式;(2)、在抛物线对称轴 上找一点 ,使 的值最大,并求出这个最大值;(3)、点 为 轴右侧抛物线上一动点,连接 ,过点 作 交 轴于点 ,问:是否存在点 使得以 , , 为顶点的三角形与 相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在抛物线对称轴 上找一点 ,使 的值最大,并求出这个最大值;(3)、点 为 轴右侧抛物线上一动点,连接 ,过点 作 交 轴于点 ,问:是否存在点 使得以 , , 为顶点的三角形与 相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.