江西省南昌市2020年中考数学一模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
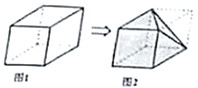
1. 19的相反数是( )A、﹣19 B、- C、 D、192. 如图所示,把图1中正方体的一个角切掉,形成了如图2的几何体,则图2的俯视图是( ).
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各式计算正确的是( ).A、 B、 C、 D、4. 对于一列数据,如果去掉一个最大值和一个最小值,那么这列数据分析一定不受影响的是( ).A、平均数 B、中位数 C、众数 D、方差5. 如图,在 的正方形网格中,能画出与“格点 ”面积相等的“格点正方形”有( )个.
3. 下列各式计算正确的是( ).A、 B、 C、 D、4. 对于一列数据,如果去掉一个最大值和一个最小值,那么这列数据分析一定不受影响的是( ).A、平均数 B、中位数 C、众数 D、方差5. 如图,在 的正方形网格中,能画出与“格点 ”面积相等的“格点正方形”有( )个.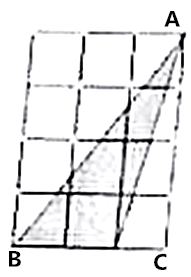 A、2 B、4 C、6 D、86. 对于二次函数 ,下列说法错误的是( ).A、该二次函数图象的对称轴可以是 轴 B、该二次函数图象的对称轴不可能是 C、当 时, 的值随 的值增大而增大 D、该二次函数图象的对称轴只能在 轴的右侧
A、2 B、4 C、6 D、86. 对于二次函数 ,下列说法错误的是( ).A、该二次函数图象的对称轴可以是 轴 B、该二次函数图象的对称轴不可能是 C、当 时, 的值随 的值增大而增大 D、该二次函数图象的对称轴只能在 轴的右侧二、填空题
-
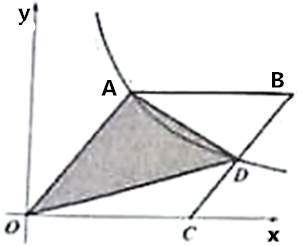
7. 计算: .8. 据北晚新视觉网3月20日报道,“新冠肺炎肆虐全球,意大利尤其严重,据民防都门预计,该国日前每月急需9000万只口罩.其中9000万用科学记数法表示为 .9. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为 斤,一只燕的重量为 斤,则可列方程为 .10. 已知 , 是方程 的两个实数根,则 的值为 .11. 已知菱形 在坐标系中如图放置,点 在 轴上,若点 坐标为 ,经过 点的双曲线交 于 ,则 的面积为 .
 12. 在 中, , ,点 是斜边 上一点,若 是等腰三角形,则线段 的长可能为 .
12. 在 中, , ,点 是斜边 上一点,若 是等腰三角形,则线段 的长可能为 .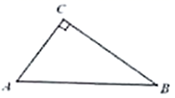
三、解答题
-
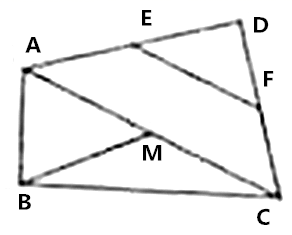
13.(1)、化简:(2)、如图,在四边形 中, , , , 分别是 , , 的中点,连接 , .求证: .
 14. 先化简,再求值: ,其中 .15. 如图,在矩形 中, , 分别是 , 边上的点,且 .若 ,试判断四边形 的形状,请说明理由.
14. 先化简,再求值: ,其中 .15. 如图,在矩形 中, , 分别是 , 边上的点,且 .若 ,试判断四边形 的形状,请说明理由.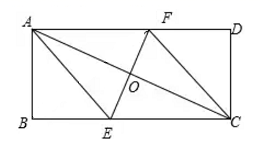 16. 《小猪佩奇》这部动画片,估计同学们都非常喜欢.周末,小猪佩奇一家4口人(小猪佩奇,小猪乔治,小猪妈妈,小猪爸爸)到一家餐厅就餐,包厢有一圆桌,旁边有四个座位( , , , ).
16. 《小猪佩奇》这部动画片,估计同学们都非常喜欢.周末,小猪佩奇一家4口人(小猪佩奇,小猪乔治,小猪妈妈,小猪爸爸)到一家餐厅就餐,包厢有一圆桌,旁边有四个座位( , , , ).
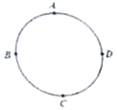 (1)、小猪佩奇随机坐到 座位的概率是;(2)、若现在由小猪佩奇,小猪乔治两人先后选座位,用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率.17. 如图,在 的正方形的网格图中,点 , , 均为格点,仅用无刻度直尺按要求作图.
(1)、小猪佩奇随机坐到 座位的概率是;(2)、若现在由小猪佩奇,小猪乔治两人先后选座位,用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率.17. 如图,在 的正方形的网格图中,点 , , 均为格点,仅用无刻度直尺按要求作图.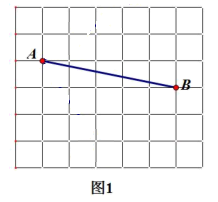
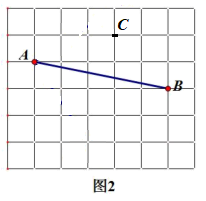 (1)、在图1中,画一条射线 ,使 ;(2)、在图2中,在线段 上求点 ,使 .18. 为了增强学生的疫情防控意识,响应“停课不停学”号召,某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校2500名学生都参加的网上测试.阅卷后,教务处随机抽取了100份答卷进行分析统计,发现考试成绩( 分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
(1)、在图1中,画一条射线 ,使 ;(2)、在图2中,在线段 上求点 ,使 .18. 为了增强学生的疫情防控意识,响应“停课不停学”号召,某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校2500名学生都参加的网上测试.阅卷后,教务处随机抽取了100份答卷进行分析统计,发现考试成绩( 分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:分数段(分)
频数(人)
频率
0.1
18
0.18
35
0.35
12
0.12
合计
100
1
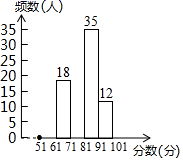 (1)、填空: , , ;(2)、将频数分布直方图补充完整;(3)、该校对成绩为 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为 ,请你估算全校获得二等奖的学生人数;(4)、结合调查的情况,为了提高疫情防控意识,请你给学校提一条合理性建议.19. 如图1,是某保温杯的实物图和平面抽象示意图.点 , 是保温杯上两个固定点,与两活动环相连,把手 与两个活动环 , 相连,现测得
(1)、填空: , , ;(2)、将频数分布直方图补充完整;(3)、该校对成绩为 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为 ,请你估算全校获得二等奖的学生人数;(4)、结合调查的情况,为了提高疫情防控意识,请你给学校提一条合理性建议.19. 如图1,是某保温杯的实物图和平面抽象示意图.点 , 是保温杯上两个固定点,与两活动环相连,把手 与两个活动环 , 相连,现测得, ,如图2,当 , , 三点共线时,恰好 .

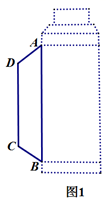 (1)、请求把手 的长;(2)、如图3,当 时,求 的度数.
(1)、请求把手 的长;(2)、如图3,当 时,求 的度数.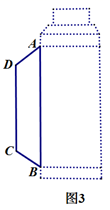
(参考数据: , , )
20. 如图, 是 的外接圆, , 交AC的延长线于点 .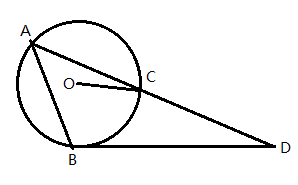 (1)、求证: 是 的切线;(2)、若 , .
(1)、求证: 是 的切线;(2)、若 , .①求 的度数;
②求 的长.
21. 数学活动课上,小明同学根据学习函数的经验,对函数的图象、性质进行了探究,下面是小明同学探究过程,请补充完整:如图1,已知在 , , , ,点 为 边上的一个动点,连接 .设 , .
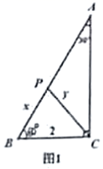 (1)、(初步感知)
(1)、(初步感知)当 时,则① , ② ;
(2)、(深入思考)试求y与x之间的函数关系式并写出自变量 的取值范围;
(3)、通过取点测量,得到了 与 的几组值,如下表:0
0.5
1
1.5
2.
2.5
3
3.5
4
2
1.8
1.7
_
2
2.3
2.6
3.0
_
①计算并补全表格(说明:补全表格时相关数值保留一位小数)
②建立平面直角坐标系,如图2,描出已补全后的表中各对应值为坐标的点,画出该函数的图象;
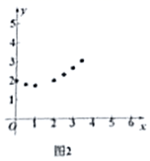
③结合画出的函数图象,写出该函数的两条性质.
22. 已知:在 中, , ,点 为 上一动点,以 为边,在 的右侧作等边 .(1)、当 平分 时,如图1,四边形 是形;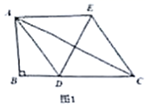 (2)、过 作 于 ,如图2,求证: 为 的中点;
(2)、过 作 于 ,如图2,求证: 为 的中点;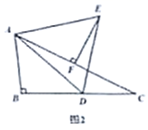 (3)、若 .
(3)、若 .①当 为 的中点时,过点 作 于 ,如图3,求 的长;
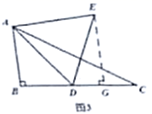
②点 从 点运动到 点,则点 所经过路径长为(直接写出结果).
23. 已知点 为抛物线 上一动点,以 为顶点,且经过原点 的抛物线,记作“ ”,设其与 轴另一交点为 ,点 的横坐标为 .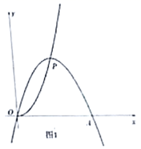
 (1)、①当 为直角三角形时,求 的值.
(1)、①当 为直角三角形时,求 的值.②当 为等边三角形时,求此时“ ”的解析式.
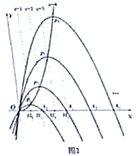
(2)、若 点的横坐标分别为1,2,3,…… ( 为正整数)时,抛物线“ ”,分别记作“ ”,“ ”…“ ”,设其与 轴另一交点分别为 , , … ,过 , , ,…, 作 轴的垂线,垂足分别为 , , ,…, .①求 的坐标和 的坐标;(用含 的代数式表示)
②当 时,求 的值;
③是否存在这样的 ,使得 ?若存在,求 的值;若不存在,说明理由.