江西省九江市2020年中考数学三模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 在负实数-5、-1、-2、-π中,最大的数是( )A、-5 B、-1 C、-2 D、-π2. 2019新型冠状病毒,因武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名“2019-nCoV”.冠状病毒是一个大型病毒家族,借助电子显微镜,我们可以看到这些病毒直径约为125纳米(1纳米=1 10-9米),125纳米用科学记数法表示等于( )米A、1.25 10-10 B、1.25 10-11 C、1.25 10-8 D、1.25 10-73.
如图所示几何体的左视图是( )
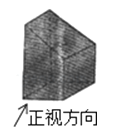 A、
A、 B、
B、 C、
C、 D、
D、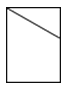 4. 江西省足协2019年第三次主席办公会在南昌召开,某学校为了激发学生对体育的热情,选拔了23名学生作为校足球队成员,其中足球队23名队员的年龄情况如表:
4. 江西省足协2019年第三次主席办公会在南昌召开,某学校为了激发学生对体育的热情,选拔了23名学生作为校足球队成员,其中足球队23名队员的年龄情况如表:年龄(岁)
12
13
14
15
16
人数(名)
3
8
6
4
2
则该校足球队队员年龄的众数和中位数分别是( )
A、13,14 B、13,13 C、14.13.5 D、16,145. 如图,矩形ABCD中, , ,将矩形ABCD绕着点A顺时针旋转得到矩形AFGE,当点F落在边CD上时,连接BF、DE,则 ( ) A、 B、 C、 D、6. 如图,抛物线 经过点 ,点 ,则下列结论:①该抛物线的对称轴为直线 ;② ;③ ;④ ,其中正确结论的个数是( )
A、 B、 C、 D、6. 如图,抛物线 经过点 ,点 ,则下列结论:①该抛物线的对称轴为直线 ;② ;③ ;④ ,其中正确结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
7. -1999-1= .8. 因式分解: = .9. 一元二次方程x2-5x+3=0的两个根为x1、x2 , 则3x1x2+x12-5x1的值为 .10. 如图,在4 x 4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中cos∠ABC= .
 11. 如图,在菱形ABCD中,AB=2,∠D=120°,将菱形翻折,使点A落在边CD的中点E处,折痕交边AD,AB于点G,F,则AF的长为
11. 如图,在菱形ABCD中,AB=2,∠D=120°,将菱形翻折,使点A落在边CD的中点E处,折痕交边AD,AB于点G,F,则AF的长为 12. 在△ABC 中,∠A=30°,∠B=90°,AC=8,点 D 在边 AB, 且 BD= ,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是 .
12. 在△ABC 中,∠A=30°,∠B=90°,AC=8,点 D 在边 AB, 且 BD= ,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是 .三、解答题
-
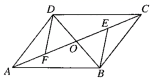
13.(1)、先化简,再求值: ÷(1+ ),其中x=2020(2)、解不等式组14. 如图, 的对角线 相交于点 分别为 的中点.求证: .
 15. 如图,是由6 6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
15. 如图,是由6 6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.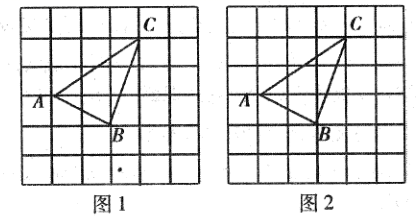 (1)、在图1中找一个格点D ,使以点A、B、C、D为顶点的四边形是平行四边形(画出一种情况即可)(2)、在图2中仅用无刻度的直尺,把线段AB三等分(保留画图痕迹,不写画法)16. 现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)、在图1中找一个格点D ,使以点A、B、C、D为顶点的四边形是平行四边形(画出一种情况即可)(2)、在图2中仅用无刻度的直尺,把线段AB三等分(保留画图痕迹,不写画法)16. 现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾. (1)、写出小明投放的垃圾恰好是“厨余垃圾”的概率;(2)、用列表法或画树状图法求小丽投放的两袋垃圾是不同类的概率17. 如图,直线y=﹣x+2与反比例函数y= 的图象相交于点A(a,3),且与x轴相交于点B.
(1)、写出小明投放的垃圾恰好是“厨余垃圾”的概率;(2)、用列表法或画树状图法求小丽投放的两袋垃圾是不同类的概率17. 如图,直线y=﹣x+2与反比例函数y= 的图象相交于点A(a,3),且与x轴相交于点B. (1)、求该反比例函数的表达式;(2)、写出直线y=﹣x+2向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标18. 近几年,随着电子产品的广泛应用,学生的近视发生率出现低龄化趋势,引起了相关部门的重视.某区为了了解在校学生的近视低龄化情况,对本区7-18岁在校近视学生进行了简单的随机抽样调查,并绘制了以下两幅不完整的统计图.
(1)、求该反比例函数的表达式;(2)、写出直线y=﹣x+2向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标18. 近几年,随着电子产品的广泛应用,学生的近视发生率出现低龄化趋势,引起了相关部门的重视.某区为了了解在校学生的近视低龄化情况,对本区7-18岁在校近视学生进行了简单的随机抽样调查,并绘制了以下两幅不完整的统计图.
请根据图中信息,回答下列问题:
(1)、这次抽样调查中共调查了近视学生人;(2)、请补全条形统计图;(3)、扇形统计图中10-12岁部分的圆心角的度数是;(4)、据统计,该区7-18岁在校学生近视人数约为10万,请估计其中7-12岁的近视学生人数.19. 如图,在△ABC中,AB=BC,以BC为直径作⊙ O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G. (1)、求证:EG是⊙O的切线;(2)、若BG=OB,AC=6,求BF的长.20. 如图1是一种纸巾盒,由盒身和圆弧盖组成,通过圆弧盖的旋转来开关纸巾盒.如图2是其侧面简化示意图,已知矩形 的长 ,宽 ,圆弧盖板侧面 所在圆的圆心 是矩形 的中心,绕点 旋转开关(所有结果保留小数点后一位).
(1)、求证:EG是⊙O的切线;(2)、若BG=OB,AC=6,求BF的长.20. 如图1是一种纸巾盒,由盒身和圆弧盖组成,通过圆弧盖的旋转来开关纸巾盒.如图2是其侧面简化示意图,已知矩形 的长 ,宽 ,圆弧盖板侧面 所在圆的圆心 是矩形 的中心,绕点 旋转开关(所有结果保留小数点后一位).
 (1)、求 所在 的半径长及 所对的圆心角度数;(2)、如图3,当圆弧盖板侧面 从起始位置 绕点 旋转 时,求 在这个旋转过程中扫过的的面积.
(1)、求 所在 的半径长及 所对的圆心角度数;(2)、如图3,当圆弧盖板侧面 从起始位置 绕点 旋转 时,求 在这个旋转过程中扫过的的面积.参考数据: , , 取3.14.
21. 赣南脐橙果大形正,肉质脆嫩,风味浓甜芳香,深受大家的喜爱.某脐橙生产基地生产的礼品盒包装的脐橙每箱的成本为30元,按定价50元出售,每天可销售200箱.为了增加销量,该生产基地决定采取降价措施,经市场调研,每降价1元,日销售量可增加20箱.
 (1)、求出每天销售量y(箱)与销售单价x(元)之间的函数关系式;(2)、若该生产基地每天要实现最大销售利润,每箱礼品盒包装的脐橙应定价多少元?每天可实现的最大利润是多少?22. 边长为4的正方形ABCD中,点E是BC边上的一个动点,连接DE,交AC于点N,过点D作DF⊥DE,交BA的延长线于点F,连接EF,交AC于点M.
(1)、求出每天销售量y(箱)与销售单价x(元)之间的函数关系式;(2)、若该生产基地每天要实现最大销售利润,每箱礼品盒包装的脐橙应定价多少元?每天可实现的最大利润是多少?22. 边长为4的正方形ABCD中,点E是BC边上的一个动点,连接DE,交AC于点N,过点D作DF⊥DE,交BA的延长线于点F,连接EF,交AC于点M.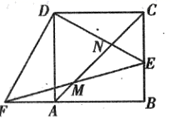 (1)、判定△DFE的形状,并说明理由;(2)、设CE=x,△AMF的面积为y,求y与x之间的函数关系式;并求出当x为何值时y有最大值?最大值是多少?(3)、随着点E在BC边上运动,NA·MC的值是否会发生变化?若不变,请求出NA·MC的值;若变化,请说明理由.23. 定义:若两条抛物线在x轴上经过两个相同点,那么我们称这两条抛物线是“同交点抛物线”,在x轴上经过的两个相同点称为“同交点”,已知抛物线y=x2 +bx+c经过(﹣2,0)、( ﹣4,0),且一条与它是“同交点抛物线”的抛物线y=ax2 +ex+f经过点( ﹣3,3).(1)、求b、c及a的值;(2)、已知抛物线y =﹣x2 +2x +3与抛物线yn= x2﹣ x﹣n (n为正整数)
(1)、判定△DFE的形状,并说明理由;(2)、设CE=x,△AMF的面积为y,求y与x之间的函数关系式;并求出当x为何值时y有最大值?最大值是多少?(3)、随着点E在BC边上运动,NA·MC的值是否会发生变化?若不变,请求出NA·MC的值;若变化,请说明理由.23. 定义:若两条抛物线在x轴上经过两个相同点,那么我们称这两条抛物线是“同交点抛物线”,在x轴上经过的两个相同点称为“同交点”,已知抛物线y=x2 +bx+c经过(﹣2,0)、( ﹣4,0),且一条与它是“同交点抛物线”的抛物线y=ax2 +ex+f经过点( ﹣3,3).(1)、求b、c及a的值;(2)、已知抛物线y =﹣x2 +2x +3与抛物线yn= x2﹣ x﹣n (n为正整数)①抛物线y和抛物线yn是不是“同交点抛物线”?若是,请求出它们的“同交点”,并写出它们一条相同的图像性质;若不是,请说明理由.
②当直线y = x+ m与抛物线y、yn , 相交共有4个交点时,求m的取值范围.
③若直线y =k(k <0)与抛物线y =﹣x2 +2x +3与抛物线yn = x2﹣ x﹣n (n为正整数)共有4个交点,从左至右依次标记为点A、点B、点C、点D,当AB =BC=CD时,求出k、n之间的关系式