江西省景德镇市乐平市区2020年中考数学一模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 计算 的结果是A、 B、7 C、 D、32. 下列手机功能标志中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 不等式组 的解集是( )A、 B、 C、 D、5. 如图所示,下列条件不能判定 的是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 不等式组 的解集是( )A、 B、 C、 D、5. 如图所示,下列条件不能判定 的是( )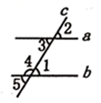 A、 B、 C、 D、6. 丽丽用手机软件记录了 天中每天所走的步数,并记录结果绘制成了如下统计表.这期间丽丽平均每天走 万步,则这组数中,众数和中位数分别是( )
A、 B、 C、 D、6. 丽丽用手机软件记录了 天中每天所走的步数,并记录结果绘制成了如下统计表.这期间丽丽平均每天走 万步,则这组数中,众数和中位数分别是( )步数/万步
5
天数
A、 , B、 , C、 , D、 ,二、填空题
-
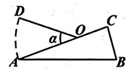
7. 石墨烯是现在世界上最薄的纳米材料,其理论厚度仅是0.00000000034m,这个数用科学记数法表示正确的是m.8. 如图是一个仰卧起坐健身器侧面示意图, 、 是支架, 是坐垫, 为靠背(可绕点 旋转), , ,当 时,点 到地面的距离为 .
( , , , , )
 9. 如图 是边长为 的等边三角形,点 从点 出发,沿 向终点 运动.作 、 、 的中点分别是 、 .点 全程运动过程中, 扫过的面积为 .
9. 如图 是边长为 的等边三角形,点 从点 出发,沿 向终点 运动.作 、 、 的中点分别是 、 .点 全程运动过程中, 扫过的面积为 .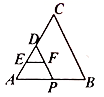 10. 已知则 ,则 的值为 .11. 已知一元二次方程 的两实数根为 和 ,则 的值为 .12. 已知 的半径为 , 是 的弦,点 在 上, .若点 到直线 的距离为 ,则 的度数为 .
10. 已知则 ,则 的值为 .11. 已知一元二次方程 的两实数根为 和 ,则 的值为 .12. 已知 的半径为 , 是 的弦,点 在 上, .若点 到直线 的距离为 ,则 的度数为 .三、解答题
-
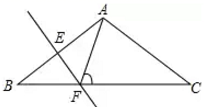
13.(1)、计算:(2)、如图,在 中, , , 的垂直平分线交 于点 ,交 于点 ,连接 ,求 的度数.
 14. 先化简,再求值: ,其中 .15. 4件同型号的产品中,有1件不合格品和3件合格品.(1)、从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;(2)、在这4件产品中加入 件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验.通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出 的值大约是多少.16. 请仅用无刻度的直尺,根据条件完成下列画图.
14. 先化简,再求值: ,其中 .15. 4件同型号的产品中,有1件不合格品和3件合格品.(1)、从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;(2)、在这4件产品中加入 件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验.通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出 的值大约是多少.16. 请仅用无刻度的直尺,根据条件完成下列画图. (1)、如图1, 内接于 , ,画出线段 的垂直平分线.(2)、如图2, 内接于 , , 、 分别为 和 的中点,画出线段 的垂直平分线.17. 在古代的《九章算术》中有一道题:今有勾五步,股 步,问勾中容方几何?意思是:如图,在 中,短直角边 步,长直角边 步,正方形有两边在两直角边上,一个顶点在斜边上.这个正方形 的边长为多少?
(1)、如图1, 内接于 , ,画出线段 的垂直平分线.(2)、如图2, 内接于 , , 、 分别为 和 的中点,画出线段 的垂直平分线.17. 在古代的《九章算术》中有一道题:今有勾五步,股 步,问勾中容方几何?意思是:如图,在 中,短直角边 步,长直角边 步,正方形有两边在两直角边上,一个顶点在斜边上.这个正方形 的边长为多少?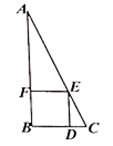 18. 如图是反比例函数 的图象,点 , 分别在图象的两支上,以 为对角线作矩形 且 轴.
18. 如图是反比例函数 的图象,点 , 分别在图象的两支上,以 为对角线作矩形 且 轴.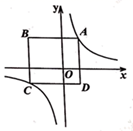 (1)、当线段 过原点时,分别写出 与 , 与 的一个等量关系式;(2)、当 、 两点在直线 上时,求矩形 的周长;(3)、当 时,探究 与 的数量关系.19. 某教育主管部门针对中小学生非统考学科的教学情况进行年终考评,抽取某校八年级部分同学的成绩作为样本,把成绩按 (优秀)、 (良好)、 (及格)、 (不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.
(1)、当线段 过原点时,分别写出 与 , 与 的一个等量关系式;(2)、当 、 两点在直线 上时,求矩形 的周长;(3)、当 时,探究 与 的数量关系.19. 某教育主管部门针对中小学生非统考学科的教学情况进行年终考评,抽取某校八年级部分同学的成绩作为样本,把成绩按 (优秀)、 (良好)、 (及格)、 (不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.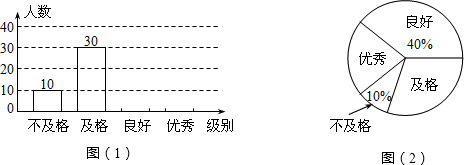 (1)、求被抽取的学生人数;(2)、补全条形统计图,并求 的圆心角度数;(3)、该校八年级有 名学生,请估计达到 、 两级的总人数.20. 某校学生食堂共有座位 个,某天午餐时,食堂中学生人数 (人)与时间 (分钟)
(1)、求被抽取的学生人数;(2)、补全条形统计图,并求 的圆心角度数;(3)、该校八年级有 名学生,请估计达到 、 两级的总人数.20. 某校学生食堂共有座位 个,某天午餐时,食堂中学生人数 (人)与时间 (分钟)变化的函数关系图象如图中的折线 .
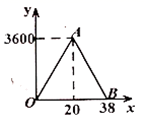 (1)、试分别求出当 与 时, 与 的函数关系式;(2)、已知该校学生数有 人,考虑到安全因素,学校决定对剩余 名同学延时用餐,即等食堂空闲座位不少于 个时,再通知剩余 名同学用餐.请结合图象分析,这 名学生至少要延时多少分钟?21. 已知 内接于 ,点 在弦 上,设 , .
(1)、试分别求出当 与 时, 与 的函数关系式;(2)、已知该校学生数有 人,考虑到安全因素,学校决定对剩余 名同学延时用餐,即等食堂空闲座位不少于 个时,再通知剩余 名同学用餐.请结合图象分析,这 名学生至少要延时多少分钟?21. 已知 内接于 ,点 在弦 上,设 , .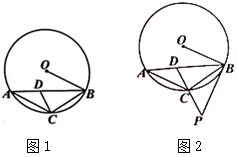 (1)、如图1,当 的半径 , 时,求 的长;(2)、如图1,试用含 的代数式表示 的大小;(3)、如图2,点 是 延长线上的一点,连接 .若 ,且 ,求证 是 的切线.22. 如图1,在矩形 中, , ,沿对角线 剪开,再把 沿 方向平移,得到图2,其中 交 于 , 交 于 .
(1)、如图1,当 的半径 , 时,求 的长;(2)、如图1,试用含 的代数式表示 的大小;(3)、如图2,点 是 延长线上的一点,连接 .若 ,且 ,求证 是 的切线.22. 如图1,在矩形 中, , ,沿对角线 剪开,再把 沿 方向平移,得到图2,其中 交 于 , 交 于 .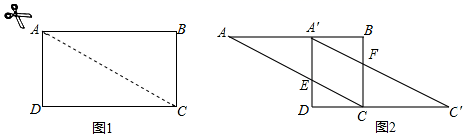 (1)、在图2中,除 与 外,指出还有哪几对全等三角形(不能添加辅助线和字母),并选择一对加以证明;(2)、设 .①当 为何值时,四边形 是菱形?②设四边形 的面积为 ,求 的最大值.23. 如图,抛物线 ( )的顶点为 ,对称轴与 轴交于点 ,当以 为对角线的正方形 的另外两个顶点 、 恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形 为它的内接正方形.
(1)、在图2中,除 与 外,指出还有哪几对全等三角形(不能添加辅助线和字母),并选择一对加以证明;(2)、设 .①当 为何值时,四边形 是菱形?②设四边形 的面积为 ,求 的最大值.23. 如图,抛物线 ( )的顶点为 ,对称轴与 轴交于点 ,当以 为对角线的正方形 的另外两个顶点 、 恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形 为它的内接正方形.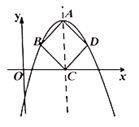 (1)、当抛物线 是美丽抛物线时,则 ;当抛物线 是美丽抛物线时,则 ;(2)、若抛物线 是美丽抛物线时,则请直接写出 , 的数量关系;(3)、若 是美丽抛物线时,(2) , 的数量关系成立吗?为什么?(4)、系列美丽抛物线 ( 为小于 的正整数)顶点在直线 上,且它们中恰有两条美丽抛物线内接正方形面积比为 .求它们二次项系数之和.
(1)、当抛物线 是美丽抛物线时,则 ;当抛物线 是美丽抛物线时,则 ;(2)、若抛物线 是美丽抛物线时,则请直接写出 , 的数量关系;(3)、若 是美丽抛物线时,(2) , 的数量关系成立吗?为什么?(4)、系列美丽抛物线 ( 为小于 的正整数)顶点在直线 上,且它们中恰有两条美丽抛物线内接正方形面积比为 .求它们二次项系数之和.