江西省抚州市2020年中考数学二模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 如图,点A表示的实数是( )
 A、﹣ B、﹣ C、1﹣ D、1﹣2. 2019年10月1日,庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行,随后举行的阅兵仪式备受国内外关注.本次阅兵仪式是新中国成立70年以来规模最大、受检阅人数最多的一次,彰显了我国强大的国防实力.央视新闻置顶的微博#国庆阅兵#在10月1日下午6点阅读次数就超过34亿.其中34亿用科学记数法可表示为( )A、0.34×109 B、3.4×108 C、3.4×109 D、34×1093. 如图是由6个棱长均为1的正方体组成的几何体,从左面看到的该几何体的形状为( )
A、﹣ B、﹣ C、1﹣ D、1﹣2. 2019年10月1日,庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行,随后举行的阅兵仪式备受国内外关注.本次阅兵仪式是新中国成立70年以来规模最大、受检阅人数最多的一次,彰显了我国强大的国防实力.央视新闻置顶的微博#国庆阅兵#在10月1日下午6点阅读次数就超过34亿.其中34亿用科学记数法可表示为( )A、0.34×109 B、3.4×108 C、3.4×109 D、34×1093. 如图是由6个棱长均为1的正方体组成的几何体,从左面看到的该几何体的形状为( ) A、
A、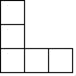 B、
B、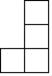 C、
C、 D、
D、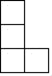 4. 下列计算正确的是( )
4. 下列计算正确的是( )
A、-(x-y)2=-x2-2xy-y2 B、(- xy2)3=- x3y6 C、x2y÷ =x2(y≠0) D、(- )-2÷ =45. 如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( ) A、AF= CF B、∠DCF=∠DFC C、图中与△AEF相似的三角形共有5个 D、tan∠CAD=6. 如图所示,抛物线L:y=ax2+bx+c(a<0)的对称轴为x=5,且与x轴的左交点为(1,0),则下列说法正确的有( )
A、AF= CF B、∠DCF=∠DFC C、图中与△AEF相似的三角形共有5个 D、tan∠CAD=6. 如图所示,抛物线L:y=ax2+bx+c(a<0)的对称轴为x=5,且与x轴的左交点为(1,0),则下列说法正确的有( )①C(9,0);②b+c>﹣10;③y的最大值为﹣16a;④若该抛物线与直线y=8有公共交点,则a的取值范围是a≤ .
 A、①②③④ B、①②③ C、①③④ D、①④
A、①②③④ B、①②③ C、①③④ D、①④二、填空题
-
7. 对于任意不相等的两个数a,b,定义一种运算※如下:a※b= ,如3※2= .那么4※8= .8. 分解因式:9m2-n2=.9. 一组数据为:5,﹣2,3,x,3,﹣2,若每个数据都是这组数据的众数,则这组数据的中位数是 .10. 如图,在菱形ABCD中,点E在对角线AC上,点F在边CD上,连接BE、EF.若∠EFC=90°+ ∠CBE,BE=7,EF=10.则点D到EF的距离为 .
 11. 如图,在矩形ABCD中,E,F,G,H分别为边AB,AD,CD,BC的中点,若AB=6,AD=8,则图中阴影部分的面积为 .
11. 如图,在矩形ABCD中,E,F,G,H分别为边AB,AD,CD,BC的中点,若AB=6,AD=8,则图中阴影部分的面积为 . 12. 如图,在平面直角坐标系中,直线y=﹣kx+m与双曲线y= (x>0)交于A、B两点,点A的横坐标为1,点B的纵坐标为2,点P是y轴上一动点,当△PAB的周长最小时,点P的坐标是 .
12. 如图,在平面直角坐标系中,直线y=﹣kx+m与双曲线y= (x>0)交于A、B两点,点A的横坐标为1,点B的纵坐标为2,点P是y轴上一动点,当△PAB的周长最小时,点P的坐标是 .
三、解答题
-
13. 计算:
 +tan60°-(sin45°)-1-|1-
+tan60°-(sin45°)-1-|1- 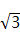 | 14. 如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x.
| 14. 如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x. (1)、求证:△PFA∽△ABE;(2)、若以P,F,E为顶点的三角形也与△ABE相似,试求x的值.15. 化简求值: ,其中 .16. 在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.(1)、从中任取一球,将球上的数字记为a,则关于x的元二次方程x2-2x-a+1=0有实数根的概率;(2)、从中任取一球,将球上的数字作为点的横坐标,记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第三象限内的概率.17. 如图,在△ABC中,AB=AC.
(1)、求证:△PFA∽△ABE;(2)、若以P,F,E为顶点的三角形也与△ABE相似,试求x的值.15. 化简求值: ,其中 .16. 在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.(1)、从中任取一球,将球上的数字记为a,则关于x的元二次方程x2-2x-a+1=0有实数根的概率;(2)、从中任取一球,将球上的数字作为点的横坐标,记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第三象限内的概率.17. 如图,在△ABC中,AB=AC. (1)、若以点A为圆心的圆与边BC相切于点D,请在下图中作出点D;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若该圆与边AC相交于点E,连接DE,当∠BAC=100°时,求∠AED的度数.18. 为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:
(1)、若以点A为圆心的圆与边BC相切于点D,请在下图中作出点D;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若该圆与边AC相交于点E,连接DE,当∠BAC=100°时,求∠AED的度数.18. 为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:
请根据以上统计图中的信息解答下列问题.
(1)、植树3株的人数为;(2)、扇形统计图中植树为1株的扇形圆心角的度数为;(3)、该班同学植树株数的中位数是(4)、小明以下方法计算出该班同学平均植树的株数是:(1+2+3+4+5)÷5=3(株),根据你所学的统计知识判断小明的计算是否正确,若不正确,请写出正确的算式,并计算出结果
19. 我市“佳禾”农场的十余种有机蔬菜在北京市场上颇具竞争力.某种有机蔬菜上市后,一经销商在市场价格为10元/千克时,从“佳禾”农场收购了某种有机蔬菜2000 千克存放入冷库中.据预测,该种蔬菜的市场价格每天每千克将上涨0.2元,但冷库存放这批蔬菜时每天需要支出各种费用合计148元,已知这种蔬菜在冷库中最多保存90天,同时,平均每天将会有6千克的蔬菜损坏不能出售.(1)、若存放x天后,将这批蔬菜一次性出售,设这批蔬菜的销售总金额为y元,试写出y与x之间的函数关系式.(2)、经销商想获得利润7200元,需将这批蔬菜存放多少天后出售?(利润=销售总金额﹣收购成本﹣各种费用)(3)、经销商将这批蔬菜存放多少天后出售可获得最大利润?最大利润是多少?20. 在平面直角坐标系xOy中,一次函数y=2x+b的图象与x轴的交点为A(2,0),与y轴的交点为B,直线AB与反比例函数y= 的图象交于点C(﹣1,m).(1)、求一次函数和反比例函数的表达式;(2)、求出关于x的不等式2x+b> 的解集;(3)、点P是这个反比例函数图象上的点,过点P作PM⊥x轴,垂足为点M,连接OP,BM,当S△ABM=2S△OMP时,求点P的坐标.21. 如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好.此时,路灯的灯柱AB的高应该设计为多少米.(结果保留根号)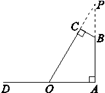 22. 如图,AB为⊙O的直径,C,D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
22. 如图,AB为⊙O的直径,C,D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.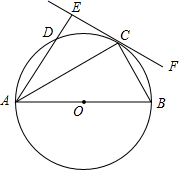 (1)、求证:EF是⊙O的切线.(2)、若∠CAO=30°,BC=2,求劣弧BC的长.23. 如图,现有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN丁点Q,连接CM.
(1)、求证:EF是⊙O的切线.(2)、若∠CAO=30°,BC=2,求劣弧BC的长.23. 如图,现有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN丁点Q,连接CM. (1)、求证:PM=PN;(2)、当P,A重合时,求MN的值;(3)、若△PQM的面积为S,求S的取值范围.24. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.
(1)、求证:PM=PN;(2)、当P,A重合时,求MN的值;(3)、若△PQM的面积为S,求S的取值范围.24. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.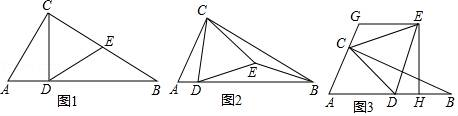 (1)、如图1,当点E在边BC上时,求证DE=EB;(2)、如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)、如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
(1)、如图1,当点E在边BC上时,求证DE=EB;(2)、如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)、如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.