上海市奉贤区2020届高三数学二模试卷
试卷更新日期:2020-06-15 类型:高考模拟
一、单选题
-
1. 某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用如图的条形图表示,根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )
 A、1.5小时 B、1.0小时 C、0.9小时 D、0.6小时2. 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线 ,终边为射线 ,过点P作直线 的垂线,垂足为M,将点M到直线 的距离表示成x的函数 ,则 在 上的图象大致为( )
A、1.5小时 B、1.0小时 C、0.9小时 D、0.6小时2. 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线 ,终边为射线 ,过点P作直线 的垂线,垂足为M,将点M到直线 的距离表示成x的函数 ,则 在 上的图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 设函数 ,其中 ,且 ,若 ,则 ( )A、1 B、a C、 D、 或a
3. 设函数 ,其中 ,且 ,若 ,则 ( )A、1 B、a C、 D、 或a二、填空题
-
4. 球的表面积为 ,则球的体积为
 . 5. 已知圆的参数方程为 ,则此圆的半径是6. 设 ( 为虚数单位),若 ,则实数7. 已知 为曲线 上位于第一象限内的点, 、 分别为 的两焦点,若 是直角,则点P坐标为8. 已知O是坐标原点,点A(﹣1,1),若点M(x,y)为平面区域 上的一个动点,则 的最大值是 .9. 从4男2女六名志愿者中任选三名参加某次公益活动,则选出的三名志愿者中既有男志愿者又有女志愿者的概率是(结果用数值表示)10. 中, ,则A的取值范围为 .11. 已知等差数列 的各项不为零,且 、 、 成等比数列,则公比是12. 如图,在正方体 中,M、N分别是 、 的中点,则异面直线 与 所成角的大小是 .
. 5. 已知圆的参数方程为 ,则此圆的半径是6. 设 ( 为虚数单位),若 ,则实数7. 已知 为曲线 上位于第一象限内的点, 、 分别为 的两焦点,若 是直角,则点P坐标为8. 已知O是坐标原点,点A(﹣1,1),若点M(x,y)为平面区域 上的一个动点,则 的最大值是 .9. 从4男2女六名志愿者中任选三名参加某次公益活动,则选出的三名志愿者中既有男志愿者又有女志愿者的概率是(结果用数值表示)10. 中, ,则A的取值范围为 .11. 已知等差数列 的各项不为零,且 、 、 成等比数列,则公比是12. 如图,在正方体 中,M、N分别是 、 的中点,则异面直线 与 所成角的大小是 . 13. 集合 , ,若 ,则实数a的取值范围是14. 三个同学对问题“已知 ,且 ,求 的最小值”提出各自的解题思路:
13. 集合 , ,若 ,则实数a的取值范围是14. 三个同学对问题“已知 ,且 ,求 的最小值”提出各自的解题思路:甲: ,可用基本不等式求解;
乙: ,可用二次函数配方法求解;
丙: ,可用基本不等式求解;
参考上述解题思路,可求得当 时, ( , )有最小值
15. 在平面直角坐标系内有两点 , , ,点 在抛物线 上, 为抛物线的焦点,若 ,则三、解答题
-
16. 如图,已知正四棱柱 中,底面边长 ,侧棱 ,过点B作 的垂线交侧棱 于点E,交 于点F.
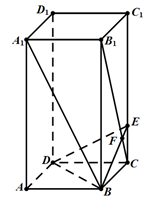 (1)、求 的长;(2)、求 与平面 所成的线面角.17. 已知向量 , ( , ),令 ( ).(1)、化简 ,并求当 时方程 的解集;(2)、已知集合 , 是函数 与 定义域的交集且 不是空集 ,判断元素 与集合 的关系,说明理由.18. 甲、乙两地相距300千米,汽车从甲地匀速行驶到乙地,速度不超过100千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度 (千米/小时)的平方成正比,比例系数为 ( ),固定部分为1000元.(1)、把全程运输成本 (元)表示为速度 (千米/小时)的函数,并指出这个函数的定义域;(2)、为了使全程运输成本最小,汽车应以多大速度行驶?19. 直线 上的动点 到点 的距离是它到点 的距离的3倍.(1)、求点P的坐标;(2)、设双曲线 的右焦点是F,双曲线经过动点P,且 ,求双曲线的方程;(3)、点 关于直线 的对称点为 ,试问能否找到一条斜率为 ( )的直线 与(2)中的双曲线 交于不同的两点 、 ,且满足 ,若存在,求出斜率 的取值范围,若不存在,请说明理由.20. 两个数列 、 ,当 和 同时在 时取得相同的最大值,我们称 与 具有性质 ,其中 .(1)、设 的二项展开式中 的系数为 ( ), ,记 , , ,依次下去, ,组成的数列是 ;同样地, 的二项展开式中 的系数为 ( ), ,记 , , ,依次下去, ,组成的数列是 ;判别 与 是否具有性质 ,请说明理由;(2)、数列 的前 项和是 ,数列 的前 项和是 ,若 与 具有性质 , ,则这样的数列 一共有多少个?请说明理由;(3)、两个有限项数列 与 满足 , ,且 ,是否存在实数 ,使得 与 具有性质 ,请说明理由.
(1)、求 的长;(2)、求 与平面 所成的线面角.17. 已知向量 , ( , ),令 ( ).(1)、化简 ,并求当 时方程 的解集;(2)、已知集合 , 是函数 与 定义域的交集且 不是空集 ,判断元素 与集合 的关系,说明理由.18. 甲、乙两地相距300千米,汽车从甲地匀速行驶到乙地,速度不超过100千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度 (千米/小时)的平方成正比,比例系数为 ( ),固定部分为1000元.(1)、把全程运输成本 (元)表示为速度 (千米/小时)的函数,并指出这个函数的定义域;(2)、为了使全程运输成本最小,汽车应以多大速度行驶?19. 直线 上的动点 到点 的距离是它到点 的距离的3倍.(1)、求点P的坐标;(2)、设双曲线 的右焦点是F,双曲线经过动点P,且 ,求双曲线的方程;(3)、点 关于直线 的对称点为 ,试问能否找到一条斜率为 ( )的直线 与(2)中的双曲线 交于不同的两点 、 ,且满足 ,若存在,求出斜率 的取值范围,若不存在,请说明理由.20. 两个数列 、 ,当 和 同时在 时取得相同的最大值,我们称 与 具有性质 ,其中 .(1)、设 的二项展开式中 的系数为 ( ), ,记 , , ,依次下去, ,组成的数列是 ;同样地, 的二项展开式中 的系数为 ( ), ,记 , , ,依次下去, ,组成的数列是 ;判别 与 是否具有性质 ,请说明理由;(2)、数列 的前 项和是 ,数列 的前 项和是 ,若 与 具有性质 , ,则这样的数列 一共有多少个?请说明理由;(3)、两个有限项数列 与 满足 , ,且 ,是否存在实数 ,使得 与 具有性质 ,请说明理由.