福建省泉州市石狮市2020年中考数学5月一模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、 B、0 C、 D、2. 自新型冠状病毒肺炎肆虑全球以来,万众一心战疫情已成为世界各国的共同语言,截止到2020年4月26日,全球感染新型冠状病毒肺炎的治愈人数已经突破858000人,将858000用科学记数法表示为( )A、 B、 C、 D、3. 下列几何体中,俯视图为三角形的是( )A、
 B、
B、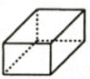 C、
C、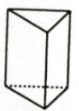 D、
D、 4. 在下列图形中,既是轴对称图形,又是中心对称图形的是( )A、等边三角形 B、直角三角形 C、正五边形 D、矩形5. 下列事件是必然事件的是( ).A、随意掷两个均匀的骰子,朝上面的点数之和为6 B、抛一枚硬币,正面朝上 C、3个人分成两组,一定有2个人分在一组 D、打开电视,正在播放动画片6. 下列运算中正确的是( )A、 B、 C、 D、7. 已知一个多边形的内角和等于900º,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形8. 实数 在数轴上的对应点的位置如图所示,若 ,则下列结论中错误的是( )
4. 在下列图形中,既是轴对称图形,又是中心对称图形的是( )A、等边三角形 B、直角三角形 C、正五边形 D、矩形5. 下列事件是必然事件的是( ).A、随意掷两个均匀的骰子,朝上面的点数之和为6 B、抛一枚硬币,正面朝上 C、3个人分成两组,一定有2个人分在一组 D、打开电视,正在播放动画片6. 下列运算中正确的是( )A、 B、 C、 D、7. 已知一个多边形的内角和等于900º,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形8. 实数 在数轴上的对应点的位置如图所示,若 ,则下列结论中错误的是( ) A、 B、 C、 D、9. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲乙经过多少日相逢?设甲乙经过x日相逢,可列方程( )A、 B、 C、 D、10. 若 是关于方程 的两个实数根,则实数 的大小关系是( )A、 B、 C、 D、
A、 B、 C、 D、9. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲乙经过多少日相逢?设甲乙经过x日相逢,可列方程( )A、 B、 C、 D、10. 若 是关于方程 的两个实数根,则实数 的大小关系是( )A、 B、 C、 D、二、填空题
-
11. 如图,直线a、b被直线l所截,a∥b,∠1=70°,则∠2= .
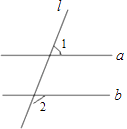 12. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:
12. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:投中次数
3
5
6
7
8
人数
1
3
2
2
2
则这些队员投中次数的众数为 .
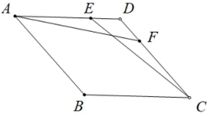
13. 如图,已知平行四边形 的对角线 与 相交于点 , ,若 , ,则 的长是 . 14. 如图在圆内接四边形 中, ,分别延长 , 交于点 ,则 的大小为 .
14. 如图在圆内接四边形 中, ,分别延长 , 交于点 ,则 的大小为 . 15. 如图,已知等边三角形 的顶点 分别在反比例函数 图像的两个分支上,点 在反比例函数y=(k≠0)的图像上,当 的面积最小时,k的值 .
15. 如图,已知等边三角形 的顶点 分别在反比例函数 图像的两个分支上,点 在反比例函数y=(k≠0)的图像上,当 的面积最小时,k的值 .
三、解答题
-
16. 解不等式组 ,并将解集在数轴上表示出来.17. 如图,在菱形 中,点 、 分别在 、 上,且 .求证: .
 18. 先化简,再求值: ,其中 .19. 如图, 中, 是 边上一点.
18. 先化简,再求值: ,其中 .19. 如图, 中, 是 边上一点.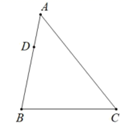 (1)、在边 上求作一点 ,使得 .(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若 的面积是 面积的9倍,且 ,求 的长.20. 如图,矩形 中, , ,将矩形 绕点 顺时针旋转 ,点 分别落在点 , , 处.
(1)、在边 上求作一点 ,使得 .(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若 的面积是 面积的9倍,且 ,求 的长.20. 如图,矩形 中, , ,将矩形 绕点 顺时针旋转 ,点 分别落在点 , , 处. (1)、直接填空:当 时,点 所经过的路径的长为;(2)、若点 , , 在同一直线上,求 的值.21. 某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每盒150元,每台新机最多可配买24盒;若非同时配买,则每盒需220元.
(1)、直接填空:当 时,点 所经过的路径的长为;(2)、若点 , , 在同一直线上,求 的值.21. 某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每盒150元,每台新机最多可配买24盒;若非同时配买,则每盒需220元.公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如表:
消耗墨盒数
22
23
24
25
打印机台数
1
4
4
1
(1)、以这十台打印机消耗墨盒数为样本,估计“一年该款打印机正常工作5年消耗的墨盒数不大于24”的概率;(2)、试以这10台打印机5年消耗的墨盒数的平均数作为决策依据,说明购买10台该款打印机时,每台应统一配买23盒墨还是24盒墨更合算?22. 某商场销售一种笔记本,进价为每本10元.试营销阶段发现:当销售单价为12元时,每天可卖出100本,如调整价格,每涨价1元,每天要少卖出10本.设该笔记本的销售单价为 元,每天获得的销售利润为 元.(1)、当 时,求 与 之间的函数关系式;(2)、当 时,求销售单价为多少元时,该笔记本每天的销售利润最大?并求出最大值.
