福建省宁德市寿宁县2020年中考数学一模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 计算: ( )A、 B、 C、2 D、12. 地球与月球的平均距离为384 000km,将384 000这个数用科学记数法表示为( )A、3.84×103 B、3.84×104 C、3.84×105 D、3.84×1063. 如图是某个几何体的三视图,该几何体是( )
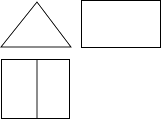 A、三棱柱 B、三棱锥 C、圆柱 D、圆锥4. 下列计算正确的是( )A、 B、 C、 D、5. 如图, ,要使 ,则 的大小是( )
A、三棱柱 B、三棱锥 C、圆柱 D、圆锥4. 下列计算正确的是( )A、 B、 C、 D、5. 如图, ,要使 ,则 的大小是( )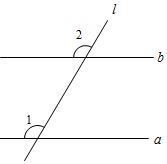 A、 B、 C、 D、6. 下列说法正确的是( )A、一组数据2,2,3,4的众数是2,中位数是2.5 B、了解某市市民知晓“礼让行人”交通新规的情况,适合全面调查 C、甲、乙两人跳远成绩的方差分别为 甲 , 乙 ,说明乙的跳远成绩比甲稳定 D、可能性是1%的事件在一次试验中一定不会发生7. 已知二元一次方程组 ,则m+n的值是( )A、1 B、0 C、-2 D、-18. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确的是( )A、 B、 C、 D、9. 如图,△ABC中,AC=4,BC=3,AB=5,AD为△ABC的角平分线,则CD的长度为( )
A、 B、 C、 D、6. 下列说法正确的是( )A、一组数据2,2,3,4的众数是2,中位数是2.5 B、了解某市市民知晓“礼让行人”交通新规的情况,适合全面调查 C、甲、乙两人跳远成绩的方差分别为 甲 , 乙 ,说明乙的跳远成绩比甲稳定 D、可能性是1%的事件在一次试验中一定不会发生7. 已知二元一次方程组 ,则m+n的值是( )A、1 B、0 C、-2 D、-18. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确的是( )A、 B、 C、 D、9. 如图,△ABC中,AC=4,BC=3,AB=5,AD为△ABC的角平分线,则CD的长度为( )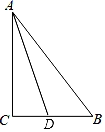 A、1 B、 C、 D、10. 若直线 经过点 ,直线 经过点 ,且 与 关于 轴对称,则 与 的交点坐标为( )A、 B、 C、 D、
A、1 B、 C、 D、10. 若直线 经过点 ,直线 经过点 ,且 与 关于 轴对称,则 与 的交点坐标为( )A、 B、 C、 D、二、填空题
-
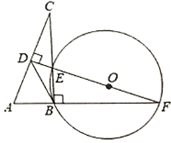
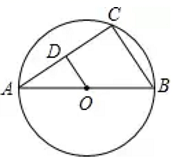
11. 计算:- = .12. 分解因式: = .13. 若AB是 的直径,AC是弦, 于点 ,若 ,则BC= .
 14. 为了满足广大师生的饮食用餐要求,学校餐厅为师生准备了A,B,C,D四种特制套餐,丁老师和小明同学一起去吃饭,他们每人随机选取一份套餐(套餐量满足师生选择需求),则丁老师和小明选到不同种套餐的概率是 .15. 如图,在正六边形 中,连接 , 交于点 ,则 °.
14. 为了满足广大师生的饮食用餐要求,学校餐厅为师生准备了A,B,C,D四种特制套餐,丁老师和小明同学一起去吃饭,他们每人随机选取一份套餐(套餐量满足师生选择需求),则丁老师和小明选到不同种套餐的概率是 .15. 如图,在正六边形 中,连接 , 交于点 ,则 °.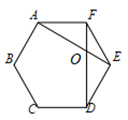 16. 已知点 为双曲线 上的一点,过点 作 轴、 轴的垂线,分别交直线 于点 、 两点(点 在点 下方.若直线 与 轴交于点 ,与 轴相交于点 ,则 的值为.
16. 已知点 为双曲线 上的一点,过点 作 轴、 轴的垂线,分别交直线 于点 、 两点(点 在点 下方.若直线 与 轴交于点 ,与 轴相交于点 ,则 的值为.三、解答题
-
17. 解不等式组 ,并把解集在数轴上表示出来.18. 如图,一块直角三角板的直角顶点P放在正方形ABCD的BC边上,并且使条直角边经过点D,另一条直角边与AB交于点Q.请写出一对相似三角形,并加以证明.(图中不添加字母和线段)
 19. 先化简,再求值: ,其中 .20. 如图,在矩形 中, .
19. 先化简,再求值: ,其中 .20. 如图,在矩形 中, . (1)、尺规作图:在线段上一点 ,使得 ,(保留作图痕迹,不写作法与证明);(2)、连接 ,若点 为边 的中点,求证: .21. 某校为响应全民阅读活动,利用节假日面向社会开放学校图书馆,据统计,第一个月进馆200人次,此后进馆人次逐月增加,到第三个月进馆达到288人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不得超过400人次,若进馆人次的月平均增长率不变,到第几个月时,进馆人数将超过学校图书馆的接纳能力,并说明理由.22. 如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
(1)、尺规作图:在线段上一点 ,使得 ,(保留作图痕迹,不写作法与证明);(2)、连接 ,若点 为边 的中点,求证: .21. 某校为响应全民阅读活动,利用节假日面向社会开放学校图书馆,据统计,第一个月进馆200人次,此后进馆人次逐月增加,到第三个月进馆达到288人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不得超过400人次,若进馆人次的月平均增长率不变,到第几个月时,进馆人数将超过学校图书馆的接纳能力,并说明理由.22. 如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.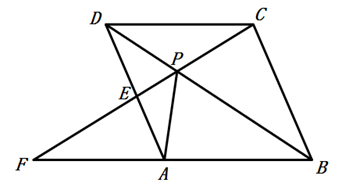 (1)、求证: .(2)、如果 ,求线段PC的长.23. 某种水果按照果径大小可分为4个等级:标准果、优质果、精品果、礼品果,某采购商从采购的一批该种水果中随机抽取100个,利用它的等级分类标准得到的数据如下:
(1)、求证: .(2)、如果 ,求线段PC的长.23. 某种水果按照果径大小可分为4个等级:标准果、优质果、精品果、礼品果,某采购商从采购的一批该种水果中随机抽取100个,利用它的等级分类标准得到的数据如下:等级
标准果
优质果
精品果
礼品果
个数
10
30
40
20
用样本估计总体,果园老板提出两种购销方案给采购商参考,
方案1:不分类卖出,售价为20元/个;
方案2:分类卖出,分类后的水果售价如下:
等级
标准果
优质果
精品果
礼品果
售价(元/个)
16
18
22
24
(1)、从采购商的角度考虑,应该采用哪种购销方案?(2)、若采购商采购的该种水果的进价不超过20元/个,则采购商可以获利,现从这种水果的4个等级中任选2种,按方案2进行购买,求这2种等级的水果至少有一种能使采购商获利的概率.