福建省福州2020年中考数学3月模拟试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 下列有理数的倒数等于﹣8的是( )A、 B、﹣ C、8 D、﹣82. 下列几何体是由4个相同的小正方体搭成的,其中左视图与主视图相同的是A、
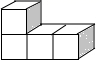 B、
B、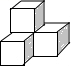 C、
C、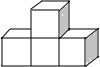 D、
D、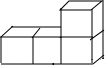 3. 下列等式成立的是( )A、x2+3x2=3x4 B、0.00028=2.8×10﹣3 C、(a3b2)3=a9b6 D、(﹣a+b)(﹣a﹣b)=b2﹣a24. 某大桥某一周的日均车流量分别为13,14,11,10,12,12,15(单位:千辆),则这组数据的中位数与众数分别为( )A、10,12 B、12,10 C、12,12 D、13,125. 若二次根式 在实数范围内有意义,则x的取值范围在数轴上表示正确的是( )A、
3. 下列等式成立的是( )A、x2+3x2=3x4 B、0.00028=2.8×10﹣3 C、(a3b2)3=a9b6 D、(﹣a+b)(﹣a﹣b)=b2﹣a24. 某大桥某一周的日均车流量分别为13,14,11,10,12,12,15(单位:千辆),则这组数据的中位数与众数分别为( )A、10,12 B、12,10 C、12,12 D、13,125. 若二次根式 在实数范围内有意义,则x的取值范围在数轴上表示正确的是( )A、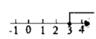 B、
B、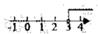 C、
C、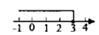 D、
D、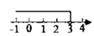 6. 一只小花猫在如图的方砖上走来走去,最终停留在阴影方砖上的概率是( )
6. 一只小花猫在如图的方砖上走来走去,最终停留在阴影方砖上的概率是( )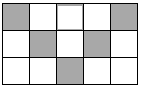 A、 B、 C、 D、7. 下列说法错误的是( )A、矩形的对角线相等 B、正方形的对称轴有四条 C、平行四边形既是中心对称图形又是轴对称图形 D、菱形的对角线互相垂直且平分8. 如图,面积为64的正方形ABCD被分成4个相同的长方形和1个面积为4的小正方形,则a,b的值分别是( )
A、 B、 C、 D、7. 下列说法错误的是( )A、矩形的对角线相等 B、正方形的对称轴有四条 C、平行四边形既是中心对称图形又是轴对称图形 D、菱形的对角线互相垂直且平分8. 如图,面积为64的正方形ABCD被分成4个相同的长方形和1个面积为4的小正方形,则a,b的值分别是( ) A、3,5 B、5,3 C、6.5,1.5 D、1.5,6.59. 如果关于 的一元二次方程 有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,错误的是( )A、方程 是倍根方程; B、若 是倍根方程,则 ; C、若方程 是倍根方程,且相异两点 都在抛物线 上,则方程 的一个根为 ; D、若点 在反比例函数 的图象上,则关于 的方程 是倍根方程.10. 如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )
A、3,5 B、5,3 C、6.5,1.5 D、1.5,6.59. 如果关于 的一元二次方程 有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,错误的是( )A、方程 是倍根方程; B、若 是倍根方程,则 ; C、若方程 是倍根方程,且相异两点 都在抛物线 上,则方程 的一个根为 ; D、若点 在反比例函数 的图象上,则关于 的方程 是倍根方程.10. 如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( ) A、20° B、25° C、30° D、40°
A、20° B、25° C、30° D、40°二、填空题
-
11. 分解因式:m4﹣81m2= .12. 如图,⊙O上有两定点A、B,点P是⊙O上一动点(不与A、B两点重合),若 ,则 的度数是 .
 13. 已知圆锥的底面半径为3,母线长为7,则圆锥的侧面积是.14. 计算:﹣2x(x2﹣ x+3)= .15. 如图,已知Rt△ABC中,∠ACB=90°,AC=8,BC=6,将△ABC绕点C顺时针旋转得到△MCN,点D、E分别为AB、MN的中点,若点E刚好落在边BC上,则sin∠DEC= .
13. 已知圆锥的底面半径为3,母线长为7,则圆锥的侧面积是.14. 计算:﹣2x(x2﹣ x+3)= .15. 如图,已知Rt△ABC中,∠ACB=90°,AC=8,BC=6,将△ABC绕点C顺时针旋转得到△MCN,点D、E分别为AB、MN的中点,若点E刚好落在边BC上,则sin∠DEC= . 16. 如图,已知反比例函数y=﹣ 的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为 .
16. 如图,已知反比例函数y=﹣ 的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为 .
三、解答题
-
17. 解方程组:
(1)、(2)、18. 如图,▱ABCD的对角线AC、BD相交于点O.你能在图中找出几对全等的三角形?证明你的结论. 19. 先化简,再求值: 其中20. 如图,△ABC中,∠C 90°,请按要求解决问题.
19. 先化简,再求值: 其中20. 如图,△ABC中,∠C 90°,请按要求解决问题. (1)、在BC边上求作一点D,使得点D到AB边的距离等于DC的长.(用尺规作图,保留作图痕迹,不写画法)(2)、若AC=6,AB=10,求△ABD的面积.21. 图1是某市2009年4月5日至14日每天最低气温的折线统计图.
(1)、在BC边上求作一点D,使得点D到AB边的距离等于DC的长.(用尺规作图,保留作图痕迹,不写画法)(2)、若AC=6,AB=10,求△ABD的面积.21. 图1是某市2009年4月5日至14日每天最低气温的折线统计图. (1)、图2是该市2007年4月5日至14日每天最低气温的频数分布直方图,根据图1提供的信息,补全图2中频数分布直方图;(2)、在这10天中,最低气温的众数是 , 中位数是 , 方差是 .(3)、请用扇形图表示出这十天里温度的分布情况.22. 随着网购的日益盛行,物流行业已逐渐成为运输业的主力,已知某大型物流公司有A、B两种型号的货车,A型货车的满载量是B型货车满载量的2倍多4吨,在两车满载的情况下,用A型货车载1400吨货物与用B型货车载560吨货物的用车数量相同.(1)、1辆A型货车和1辆B型货车的满载量分别是多少?(2)、该物流公司现有120吨货物,可以选择上述两种货车运送,在满载的情况下,有几种方案可以一次性运完?23. 如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且AD•AO=AM•AP.
(1)、图2是该市2007年4月5日至14日每天最低气温的频数分布直方图,根据图1提供的信息,补全图2中频数分布直方图;(2)、在这10天中,最低气温的众数是 , 中位数是 , 方差是 .(3)、请用扇形图表示出这十天里温度的分布情况.22. 随着网购的日益盛行,物流行业已逐渐成为运输业的主力,已知某大型物流公司有A、B两种型号的货车,A型货车的满载量是B型货车满载量的2倍多4吨,在两车满载的情况下,用A型货车载1400吨货物与用B型货车载560吨货物的用车数量相同.(1)、1辆A型货车和1辆B型货车的满载量分别是多少?(2)、该物流公司现有120吨货物,可以选择上述两种货车运送,在满载的情况下,有几种方案可以一次性运完?23. 如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且AD•AO=AM•AP. (1)、连接OP,证明:△ADM∽△APO;(2)、证明:PD是⊙O的切线;(3)、若AD=12,AM=MC,求PB和DM的值.24. 矩形ABCD中,点P在对角线BD上(点P不与点B重合),连接AP,过点P作PE⊥AP交直线BC于点E.
(1)、连接OP,证明:△ADM∽△APO;(2)、证明:PD是⊙O的切线;(3)、若AD=12,AM=MC,求PB和DM的值.24. 矩形ABCD中,点P在对角线BD上(点P不与点B重合),连接AP,过点P作PE⊥AP交直线BC于点E. (1)、如图1,当AB=BC时,猜想线段PA和PE的数量关系:;(2)、如图2,当AB≠BC时.求证:(3)、若AB=8,BC=10,以AP,PE为边作矩形APEF,连接BF,当PE= 时,直接写出线段BF的长.25. 如图,已知抛物线y= x2+bx+c过点A(3, 0)、点B(0, 3).点M(m , 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P , 与抛物线交于点Q , 联结BQ .
(1)、如图1,当AB=BC时,猜想线段PA和PE的数量关系:;(2)、如图2,当AB≠BC时.求证:(3)、若AB=8,BC=10,以AP,PE为边作矩形APEF,连接BF,当PE= 时,直接写出线段BF的长.25. 如图,已知抛物线y= x2+bx+c过点A(3, 0)、点B(0, 3).点M(m , 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P , 与抛物线交于点Q , 联结BQ .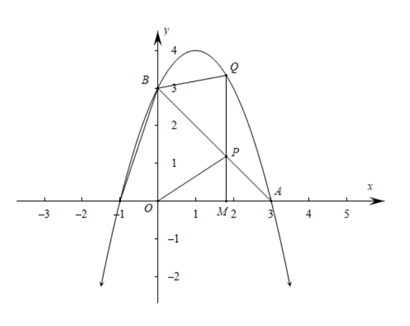 (1)、求抛物线表达式;(2)、联结OP , 当∠BOP=∠PBQ时,求PQ的长度;(3)、当△PBQ为等腰三角形时,求m的值.
(1)、求抛物线表达式;(2)、联结OP , 当∠BOP=∠PBQ时,求PQ的长度;(3)、当△PBQ为等腰三角形时,求m的值.