山西省兴县三中2019年中考数学三模试卷
试卷更新日期:2020-06-15 类型:中考模拟
一、单选题
-
1. 山西省某地2019年1月的某一天的气温最高是 6℃ ,最低是 -3℃ ,则这天该地的温差是( )A、-6℃ B、-3℃ C、3℃ D、9℃2. 晋剧即山西梆子,是我国的国粹,是介绍、传播中国传统艺术文化的重要媒介.在下面的四个晋剧脸谱中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 某校九年级1班的同学毕业时都将自己的生活照片向全班其他同学各送一张表示留念,全班共送1540张照片,求全班的学生人数.设全班有 名学生,根据题意,列出方程为( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 某校九年级1班的同学毕业时都将自己的生活照片向全班其他同学各送一张表示留念,全班共送1540张照片,求全班的学生人数.设全班有 名学生,根据题意,列出方程为( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、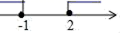 D、
D、 6. 如图,点 分别是 边 , 的中点,连接 .若 , ,则 等于( )
6. 如图,点 分别是 边 , 的中点,连接 .若 , ,则 等于( ) A、50° B、60° C、70° D、80°7. 在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )
A、50° B、60° C、70° D、80°7. 在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( ) A、27 B、51 C、69 D、728. 围棋是中国起源很早的传统文化游戏之一.它的玩法从草创到现在的样式,有一个逐渐演变的过程,在一个不透明的罐子里装有若干个白色的围棋子,现要估计白棋子的个数,王叔叔从装黑棋子的罐子里取出10个黑棋子放入白棋子的罐子里.这些棋子除颜色外其他完全相同.将罐子里的棋子搅匀,从中随机摸出一个棋子,记下颜色后再放回袋中,不断地重复这个过程,摸了200次后,发现有25次摸到黑棋子,请你估计这个罐子里装有的白棋子有( )A、80个 B、75个 C、70个 D、60个9. 如图,在 中, ,点 在 上,以点 为圆心, 为半径作 ,点 恰好在 上, 是 的切线,则 的度数是( )
A、27 B、51 C、69 D、728. 围棋是中国起源很早的传统文化游戏之一.它的玩法从草创到现在的样式,有一个逐渐演变的过程,在一个不透明的罐子里装有若干个白色的围棋子,现要估计白棋子的个数,王叔叔从装黑棋子的罐子里取出10个黑棋子放入白棋子的罐子里.这些棋子除颜色外其他完全相同.将罐子里的棋子搅匀,从中随机摸出一个棋子,记下颜色后再放回袋中,不断地重复这个过程,摸了200次后,发现有25次摸到黑棋子,请你估计这个罐子里装有的白棋子有( )A、80个 B、75个 C、70个 D、60个9. 如图,在 中, ,点 在 上,以点 为圆心, 为半径作 ,点 恰好在 上, 是 的切线,则 的度数是( )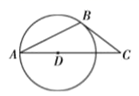 A、35° B、30° C、25° D、20°10. 如图,以矩形OABC的长OC作x轴,以宽OA作y轴建立平面直角坐标系,OA=4,OC=8,现作反比例函数 交BC于点E,交AB于点F,沿EF折叠,点B落在OC的点G处, ,则k的值是( )
A、35° B、30° C、25° D、20°10. 如图,以矩形OABC的长OC作x轴,以宽OA作y轴建立平面直角坐标系,OA=4,OC=8,现作反比例函数 交BC于点E,交AB于点F,沿EF折叠,点B落在OC的点G处, ,则k的值是( ) A、8 B、12 C、15 D、16
A、8 B、12 C、15 D、16二、填空题
-
11. 因式分解:12. 已知 两点都在反比例函数 的图象上,且 ,则 (填“>”或“<”)13. 如图,在平面直角坐标系中,已知 ,将线段 绕着点 逆时针旋转90°得到线段 ,则 的坐标为
 14. 意大利数学家斐波那契提出过一个非常有趣的数学问题:如果1对小兔每月能生1对新兔,每1对新兔在出生后的第3个月开始又生1对新兔,假定不发生死亡的情况下,1对兔子在一年内能繁殖成多少对?我们来做下面的分析:假定今年1月份生的1对兔子,今年2月份还是只有1对,到3月份这对兔子生了1对,总共两对;到4月份又可生出1对新兔,共3对;到5月份,有两对兔子生出两对新兔,加上原来的3对,共5对兔子;…假设兔子不会死去,今年10月份共有对兔子.15. 如图,在半径为 的扇形 中, ,点 在 上,且 ,过点 作 于点 ,则图中阴影部分的面积为
14. 意大利数学家斐波那契提出过一个非常有趣的数学问题:如果1对小兔每月能生1对新兔,每1对新兔在出生后的第3个月开始又生1对新兔,假定不发生死亡的情况下,1对兔子在一年内能繁殖成多少对?我们来做下面的分析:假定今年1月份生的1对兔子,今年2月份还是只有1对,到3月份这对兔子生了1对,总共两对;到4月份又可生出1对新兔,共3对;到5月份,有两对兔子生出两对新兔,加上原来的3对,共5对兔子;…假设兔子不会死去,今年10月份共有对兔子.15. 如图,在半径为 的扇形 中, ,点 在 上,且 ,过点 作 于点 ,则图中阴影部分的面积为
三、解答题
-
16.(1)、计算(2)、先化简,再求值: ,其中 .17. 如图,在 中,直线 是 的垂直平分线.
 (1)、尺规作图:作 的平分线交直线 于点 ,过点 作 的垂线交 于点 ;(2)、在(1)的图中,求证 .18. 小岛A在港口P的南偏西45°方向,距离港口81海里处.甲船从 出发,沿 方向以6海里/时的速度驶向港口,乙船从港口 出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发.
(1)、尺规作图:作 的平分线交直线 于点 ,过点 作 的垂线交 于点 ;(2)、在(1)的图中,求证 .18. 小岛A在港口P的南偏西45°方向,距离港口81海里处.甲船从 出发,沿 方向以6海里/时的速度驶向港口,乙船从港口 出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发. (1)、出发后小时两船与港口 的距离相等;(2)、出发几小时后乙船在甲船的正东方向?(结果精确到0.1小时,参考数据:19. 当前,我省大气污染防治形势依然严峻,特别是秋冬季重污染天气频繁发生,成为空气质量改善的重点和难点.某小区响应太原市提出的“建绿透绿”号召,购买了银杏树和玉兰树共150棵用来美化小区环境,购买银杏树用了12000元,购买玉兰树用了9000元.已知玉兰树的单价是银杏树单价的1.5倍,那么银杏树和玉兰树的单价各是多少?20. 某县教育局为了对该区八年级数学学科教学质量进行检查,对该区八年级的学生进行摸底,为了解摸底的情况,进行了抽样调查,过程如下,请将有关问题补充完整.
(1)、出发后小时两船与港口 的距离相等;(2)、出发几小时后乙船在甲船的正东方向?(结果精确到0.1小时,参考数据:19. 当前,我省大气污染防治形势依然严峻,特别是秋冬季重污染天气频繁发生,成为空气质量改善的重点和难点.某小区响应太原市提出的“建绿透绿”号召,购买了银杏树和玉兰树共150棵用来美化小区环境,购买银杏树用了12000元,购买玉兰树用了9000元.已知玉兰树的单价是银杏树单价的1.5倍,那么银杏树和玉兰树的单价各是多少?20. 某县教育局为了对该区八年级数学学科教学质量进行检查,对该区八年级的学生进行摸底,为了解摸底的情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据:随机抽取 学校与 学校的各20名学生的数学成绩(单位:分)进行分析:
学校
91
89
77
86
71
31
97
93
72
91
81
92
85
85
95
88
88
90
44
91
学校
84
93
66
69
76
87
77
82
85
88
90
88
67
88
91
96
68
97
59
88
(1)、整理、描述数据:按如下数据段整理、描述这两组数据分段
学校
30≤x≤39
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
学校
1
1
0
0
3
7
8
学校
(2)、分析数据:两组数据的平均数、中位数、众数、方差如下表:统计量
学校
平均数
中位数
众数
方差
学校
81.85
88
91
268.43
学校
81.95
86
m
115.25
(3)、得出结论::若 学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
:根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)
21. 请阅读下列材料,并完成相应的任务.古希腊几何学家海伦,在数学史上以解决几何测量问题而闻名.在他的著作《度量》一书中,给出了三角形面积的计算公式(海伦公式):如果一个三角形的三边长分别为 ,记 ,那么三角形的面积是 .
印度算术家波罗摩笈多和婆什迦罗还给出了四边形面积的计算公式:如果一个四边形的四边长分别为 ,记 ,那么四边形的面积是 (其中, 和 表示四边形的一组对角的度数)

根据上述信息解决下列问题:
(1)、已知三角形的三边是4,6,8,则这个三角形的面积是(2)、小明的父亲是工程师,设计的某个零件的平面图是如图的四边形 ,已知 , , , , , .求出这个零件平面图的面积.22. 综合与实践在数学活动课上,老师给出 , , .点 为 的中点,点 在射线DC上运动,将线段DE绕点D逆时针旋转90°得到线段DF,连接EF,CE.过点F作 ,交直线AB于点H.
 (1)、若点 在线段 上,如图1,
(1)、若点 在线段 上,如图1,①根据题意补全图1(不要求尺规作图);
②判断 与 的数量关系并加以证明;
(2)、若点 为线段 的延长线上一点,如图2,且 , ,补全图2,求 的面积.23. 综合与探究如图,抛物线 与 轴交于 两点,与 轴交于点 .点 是射线 上一点,过点 作直线 ,与 轴右侧的抛物线交于点 .点 从点 出发,沿射线 以每秒1个单位长度的速度向右运动,设点 运动的时间为t秒.请解答下列问题:
 (1)、求直线AC的表达式与点 的坐标;(2)、在点 运动的过程中,若以点 , , , 为顶点的四边形是平行四边形,求运动的时间 ;(3)、设点 与点 关于直线 对称,
(1)、求直线AC的表达式与点 的坐标;(2)、在点 运动的过程中,若以点 , , , 为顶点的四边形是平行四边形,求运动的时间 ;(3)、设点 与点 关于直线 对称,①点 的坐标为 (用含 的代数式表示,结果需化简);
②当点 落在抛物线 的对称轴上且点 在线段 上时,在平面内是否存在点F,使得以点 , , ,F为顶点的四边形为菱形?若存在,请求出此时点F的坐标;若不存在,请说明理由.