内蒙古包头市2020届高三理数第一次模拟考试试卷
试卷更新日期:2020-06-15 类型:高考模拟
一、单选题
-
1. 设集合 ,则 ( )A、 B、 C、 D、2. 已知i是虚数单位,若 ,则 ( )A、 B、2 C、 D、103. 设等差数列 的前 项和为 ,若 ,则 ( )A、23 B、25 C、28 D、294. 曲线 在点 处的切线方程为 ,则 ( )A、 B、 C、4 D、85. 当 时,函数 的图象大致是( )A、
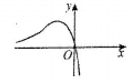 B、
B、 C、
C、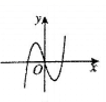 D、
D、 6. 已知定点 都在平面 内,定点 是 内异于 的动点,且 ,那么动点C在平面 内的轨迹是( )A、圆,但要去掉两个点 B、椭圆,但要去掉两个点 C、双曲线,但要去掉两个点 D、抛物线,但要去掉两个点7. 小张家订了一份报纸,送报人可能在早上 之间把报送到小张家,小张离开家去工作的时间在早上 之间.用 表示事件:“小张在离开家前能得到报纸”,设送报人到达的时间为x,小张离开家的时间为y, 看成平面中的点,则用几何概型的公式得到事件A的概率 等于( )A、 B、 C、 D、8. 在 中, 为 边上的中线,E为 的中点,且 , ,则 ( )A、 B、 C、 D、9. 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值 ,这就是著名的“徽率”。如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的 值为( )(参考数据: )
6. 已知定点 都在平面 内,定点 是 内异于 的动点,且 ,那么动点C在平面 内的轨迹是( )A、圆,但要去掉两个点 B、椭圆,但要去掉两个点 C、双曲线,但要去掉两个点 D、抛物线,但要去掉两个点7. 小张家订了一份报纸,送报人可能在早上 之间把报送到小张家,小张离开家去工作的时间在早上 之间.用 表示事件:“小张在离开家前能得到报纸”,设送报人到达的时间为x,小张离开家的时间为y, 看成平面中的点,则用几何概型的公式得到事件A的概率 等于( )A、 B、 C、 D、8. 在 中, 为 边上的中线,E为 的中点,且 , ,则 ( )A、 B、 C、 D、9. 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值 ,这就是著名的“徽率”。如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的 值为( )(参考数据: ) A、48 B、36 C、24 D、1210. 已知 是双曲线 的左、右焦点, 是C的左、右顶点,点P在过 且斜率为 的直线上, 为等腰三角形, ,则C的渐近线方程为( )A、 B、 C、 D、11. 棱长为2的正方体 内有一个内切球O,过正方体中两条异面直线 , 的中点 作直线,则该直线被球面截在球内的线段的长为( )A、 B、 C、 D、112. 设 是定义域为 的偶函数,且在 单调递增, ,则( )A、 B、 C、 D、
A、48 B、36 C、24 D、1210. 已知 是双曲线 的左、右焦点, 是C的左、右顶点,点P在过 且斜率为 的直线上, 为等腰三角形, ,则C的渐近线方程为( )A、 B、 C、 D、11. 棱长为2的正方体 内有一个内切球O,过正方体中两条异面直线 , 的中点 作直线,则该直线被球面截在球内的线段的长为( )A、 B、 C、 D、112. 设 是定义域为 的偶函数,且在 单调递增, ,则( )A、 B、 C、 D、二、填空题
-
13. 已知多项式 的各项系数之和为32,则展开式中含x项的系数为 .14. 已知抛物线 的焦点为F,斜率为2的直线l与C的交点为A,B,若 =5,则直线l的方程为 .15. 若函数 在 和 上均单调递增,则实数m的取值范围为 .
三、双空题
-
16. 分形几何学是数学家伯努瓦·曼得尔布罗在20世纪70年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图甲所示的分形规律可得如图乙所示的一个树形图:记图乙中第 行黑圈的个数为 ,则
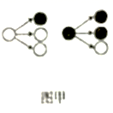
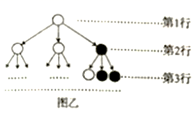 (1)、 ;(2)、 .
(1)、 ;(2)、 .四、解答题
-
17. 在 中,角 的对边分别为 ,且 .(1)、求角A的大小;(2)、已知 外接圆半径 ,求 的周长.18. 如图,三棱柱 中,侧面 是菱形,其对角线的交点为O,且 .
 (1)、求证: 平面 ;(2)、设 ,若直线 与平面 所成的角为 ,求二面角 的正弦值.19. 某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:
(1)、求证: 平面 ;(2)、设 ,若直线 与平面 所成的角为 ,求二面角 的正弦值.19. 某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下: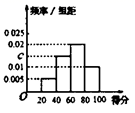
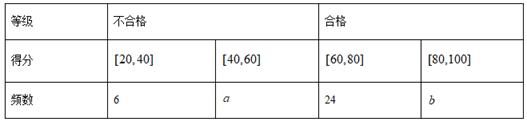 (1)、由该题中频率分布直方图求测试成绩的平均数和中位数;(2)、其他条件不变,在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;(3)、用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为 ,求 的数学期望 .20. 已知椭圆 的右焦点为 ,过点 且与x轴垂直的直线被椭圆截得的线段长为 ,且 与短轴两端点的连线相互垂直.(1)、求椭圆C的方程;(2)、若圆 上存在两点M,N,椭圆 上存在两个点 满足: 三点共线, 三点共线,且 ,求四边形 面积的取值范围.21. 已知函数 .(1)、若函数 在 上单调递增,求实数a的值;(2)、定义:若直线 与曲线 都相切,我们称直线 为曲线 、 的公切线,证明:曲线 与 总存在公切线.
(1)、由该题中频率分布直方图求测试成绩的平均数和中位数;(2)、其他条件不变,在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;(3)、用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为 ,求 的数学期望 .20. 已知椭圆 的右焦点为 ,过点 且与x轴垂直的直线被椭圆截得的线段长为 ,且 与短轴两端点的连线相互垂直.(1)、求椭圆C的方程;(2)、若圆 上存在两点M,N,椭圆 上存在两个点 满足: 三点共线, 三点共线,且 ,求四边形 面积的取值范围.21. 已知函数 .(1)、若函数 在 上单调递增,求实数a的值;(2)、定义:若直线 与曲线 都相切,我们称直线 为曲线 、 的公切线,证明:曲线 与 总存在公切线.
-