安徽省六校教育研究会2020届高三理数第二次素质测试试卷
试卷更新日期:2020-06-15 类型:高考模拟
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 已知复数 满足: ( 为虚数单位),则 ( )A、 B、 C、 D、3. 为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为 .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目
种植业
养殖业
工厂就业
服务业
参加用户比
脱贫率
那么 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A、 倍 B、 倍 C、 倍 D、 倍4. 函数 在 上的大致图象是( )A、 B、
B、 C、
C、 D、
D、 5. 已知双曲线 的右焦点为 为坐标原点,以 为直径的圆与双 曲线C的一条渐近线交于点O及点 ,则双曲线C的方程为( )A、 B、 C、 D、6. 已知实数 满足不等式组 ,则 的最小值为( )A、2 B、3 C、4 D、57. 已知某几何体的三视图如图所示,则该几何体外接球的表面积为( )
5. 已知双曲线 的右焦点为 为坐标原点,以 为直径的圆与双 曲线C的一条渐近线交于点O及点 ,则双曲线C的方程为( )A、 B、 C、 D、6. 已知实数 满足不等式组 ,则 的最小值为( )A、2 B、3 C、4 D、57. 已知某几何体的三视图如图所示,则该几何体外接球的表面积为( ) A、 B、 C、 D、8. 《易经》包含着很多哲理,在信息学、天文学中都有广泛的应用,《易经》的博大精深,对今天 的几何学和其它学科仍有深刻的影响.下图就是易经中记载的几何图形——八卦田,图中正八 边形代表八卦,中间的圆代表阴阳太极图,八块面积相等的曲边梯形代表八卦田.已知正八边 形的边长为 ,阴阳太极图的半径为 ,则每块八卦田的面积约为( )
A、 B、 C、 D、8. 《易经》包含着很多哲理,在信息学、天文学中都有广泛的应用,《易经》的博大精深,对今天 的几何学和其它学科仍有深刻的影响.下图就是易经中记载的几何图形——八卦田,图中正八 边形代表八卦,中间的圆代表阴阳太极图,八块面积相等的曲边梯形代表八卦田.已知正八边 形的边长为 ,阴阳太极图的半径为 ,则每块八卦田的面积约为( ) A、 B、 C、 D、9. 已知数列 中, ,且当 为奇数时, ;当n为偶数时, .则此数列的前20项的和为( )A、 B、 C、 D、10. 函数 的部分图象如图所示,已知 ,函数 的图象可由 图象向右平移 个单位长度而得到,则函数 的解析式为( )A、 B、 C、 D、11. 已知函数 ,若 时, 恒成立,则实数 的值为( )A、 B、 C、 D、12. 如图,棱长为l的正方体 中,P为线段 的中点, 分别为线段 和 棱 上任意一点,则 的最小值为( )
A、 B、 C、 D、9. 已知数列 中, ,且当 为奇数时, ;当n为偶数时, .则此数列的前20项的和为( )A、 B、 C、 D、10. 函数 的部分图象如图所示,已知 ,函数 的图象可由 图象向右平移 个单位长度而得到,则函数 的解析式为( )A、 B、 C、 D、11. 已知函数 ,若 时, 恒成立,则实数 的值为( )A、 B、 C、 D、12. 如图,棱长为l的正方体 中,P为线段 的中点, 分别为线段 和 棱 上任意一点,则 的最小值为( )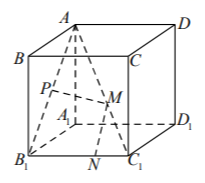 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
13. 已知正项等比数列 中, ,则 .14. 的二项展开式中,含 项的系数为 .15. 如图,两个同心圆O的半径分别为 和 , 为大圆O的一条 直径,过点B 作小圆O的切线交大圆于另一点C,切点为M,点P为劣弧 上的任一点(不包括 两点),则 的最大值是 .
 16. 已知两动点 在椭圆 上,动点P在直线 上,若 恒为锐角,则椭圆C的离心率的取值范围为 .
16. 已知两动点 在椭圆 上,动点P在直线 上,若 恒为锐角,则椭圆C的离心率的取值范围为 .三、解答题
-
17. 的内角 的对边分别为 ,若(1)、求角 的大小(2)、若 ,求的周长18. 如图,四棱锥 中,侧面 为等腰直角三角形, 平面 .
 (1)、求证: 平面 ;(2)、求直线 与平面 所成的角的正弦值.19. 已知抛物线 的焦点为F,点 ,点P为抛物线C上的动点.(1)、若 的最小值为5,求实数a的值;(2)、设线段 的中点为 ,其中 为坐标原点,若 ,求 的面积.20. 已知函数 ,直线 是曲线 在 处的切线.(1)、求证:无论实数 取何值,直线 恒过定点,并求出该定点的坐标;(2)、若直线 经过点 ,试判断函数 的零点个数并证明.21. 某工厂生产某种电子产品,每件产品不合格的概率均为 ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验 件该产品,且每 件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检 验方案:将产品每 个 一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验1次或 次.设该工厂生产1000件该产品,记每件产品的平均检验次 数为X.(1)、求X的分布列及其期望;(2)、(i)试说明,当 越小时,该方案越合理,即所需平均检验次数越少;
(1)、求证: 平面 ;(2)、求直线 与平面 所成的角的正弦值.19. 已知抛物线 的焦点为F,点 ,点P为抛物线C上的动点.(1)、若 的最小值为5,求实数a的值;(2)、设线段 的中点为 ,其中 为坐标原点,若 ,求 的面积.20. 已知函数 ,直线 是曲线 在 处的切线.(1)、求证:无论实数 取何值,直线 恒过定点,并求出该定点的坐标;(2)、若直线 经过点 ,试判断函数 的零点个数并证明.21. 某工厂生产某种电子产品,每件产品不合格的概率均为 ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验 件该产品,且每 件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检 验方案:将产品每 个 一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验1次或 次.设该工厂生产1000件该产品,记每件产品的平均检验次 数为X.(1)、求X的分布列及其期望;(2)、(i)试说明,当 越小时,该方案越合理,即所需平均检验次数越少;(ii)当 时,求使该方案最合理时 的值及 件该产品的平均检验次数.