江西省萍乡市2018-2019学年七年级下学期数学期末试卷
试卷更新日期：2020-06-12 类型：期末考试
一、选择题
-
1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列计算正确的是（ ）A、x2+x2＝x4 B、﹣x2+（2x）2＝3x2 C、x2•x3＝x6 D、2x2•x3＝4x53. 2008年1月11日，埃科学研究中心在浙江大学成立，“埃“是一个长度单位，是一个用来衡量原子间距离的长度单位．同时，“埃”还是一位和诺贝尔同时代的从事基础研究的瑞典著名科学家的名字，这代表埃科学研究中心的研究要有较为深刻的理论意义．十“埃”等于1纳米，已知：1纳米＝10﹣9米，那么：一“埃”用科学记数法表示为（ ）A、10×10﹣9米 B、1×10﹣9米 C、10×10﹣10米 D、1×10﹣10米4. 下列各式能用平方差公式计算的是（ ）①（x﹣2y）（2y+x）；
②（x﹣2y）（﹣x﹣2y）；
③（﹣x﹣2y）（x+2y）；
④（x﹣2y）（﹣x+2y）．
A、①② B、②③ C、①③ D、③④5. 书包里有数学书3本，语文书5本，英语书2本；从中任意抽取1本，则抽到数学书的概率是（ ）A、 B、 C、 D、6. 如图，已知AD∥BC，∠B＝25°，DB平分∠ADE，则∠DEC等于（ ）
A、25° B、50° C、75° D、100°7. 下列长度的线段能组成三角形的是（ ）A、2，3，5 B、4，4，8 C、14，6，7 D、15，10，98. 如图，在△ABC和△DEF中，∠B＝∠DEF，AB＝DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（ ）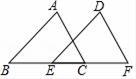
A、∠A＝∠D B、BC＝EF C、AC＝DF D、∠ACB＝∠F9. 甲、乙两人在一次百米赛跑中，路程s（米）与赛跑时间t（秒）的关系如图，则下列说法正确的是（ ）
A、乙先到达终点 B、乙比甲跑的路程多 C、乙用的时间短 D、甲的速度比乙的速度快10. 等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（ ）
A、60° B、120° C、60°或150° D、60°或120°二、填空题
-
11. 计算：（x2﹣2xy）÷x＝ ．12. 角α等于它的余角的一半，则角α的度数是°．13. 若a2＋b2＝5，ab＝2，则(a＋b)2＝.14. 某班有男生和女生各若干，若随机抽取1人，抽到男生的概率是0.4，则抽到女生的概率是 ．15. 如图，△ABC中，∠BAC＝98°，EF，MN分别为AB，AC的垂直平分线，∠FAN＝ ．
16. 李冰买了一张30元的租碟卡，每租一张碟后卡中剩余金额y（元）与租碟张数x（张）之间的关系式为租碟数/张
卡中余额/元
1
30﹣0.8
2
30﹣1.6
3
30﹣2.4
…
…
17. 如图，直线AB∥CD，E为直线AB上一点，EH，EM分别交直线CD与点F、M，EH平分∠AEM，MN⊥AB，垂足为点N，∠CFH＝α，∠EMN＝（用含α的式子表示）
18. 如图所示，∠E＝∠F＝90°，∠B＝∠C，AE＝AF．给出下列结论：①∠1＝∠2；②BE＝CF；③△ACN≌△ABM；④CD＝DN．其中正确的结论是 ． （将你认为正确的结论的序号都填上）
三、（本大题共3个题，第19题8分，第20，21题各5分，共18分）
-
19. 计算：(1)、2﹣2+（﹣3）0+（﹣0.5）2019×22019；(2)、先化简，再求值：（2x﹣1）（x+3）﹣（x﹣2）2 ， 其中x＝1．20. 已知：钝角△ABC．
(1)、作出△ABC中的BC边上的高AD；(2)、以AD所在直线为对称轴，作出△ABC的轴对称图形△AB′C′．21. 刘大伯种植了很多优质草莓，有一天，他带上若干千克草莓进城出售．为了方便，刘大伯带了一些零钱备用，刚开始销售很好，后来降价出售，如图表示刘大伯手中的钱y（元）与出售草莓的重量x（千克）之间的关系．请你结合图形回答下列问题：
(1)、刘大伯自带的零用钱是多少元？(2)、降价前，每千克草莓的出售价是多少元？(3)、降价后，刘大伯按每千克16元将剩下的草莓售完，这时他手中的钱有330元（含零用钱），则此次出售刘大伯共带了多少千克草莓？四、（本大题共2个小题，每小题5分，共10分）
-
22. 如图，在△ABC中，AB＝AC，DE垂直平分AB．
(1)、若AB＝AC＝10cm，BC＝6cm，求△BCE的周长；(2)、若∠A＝40°，求∠EBC的度数．23. 某景区7月1日﹣7月7日一周天气预报如图，小丽打算选择这期间的一天或两天去该景区旅游，求下列事件的概率：某景区一周天气预报
日期
天气
7月1日
晴
7月2日
晴
7月3日
雨
7月4日
阴
7月5日
晴
7月6日
晴
7月7日
阴
(1)、随机选择一天，恰好天气预报是晴的概率；(2)、随机选择连续的两天，恰好天气预报都是晴．五、（本大题共2个小题，第4题5分，第25题6分，共11分）
-
24. 已知：如图AB∥DE，AB＝DE，BE＝CF，此时AC与DF有什么关系？试说明理由．
25. 王勇和李华一起做风筝，选用细木棒做成如图所示的“筝形”框架，要求AB＝AD，BC＝CD，AB＞BC．
(1)、观察此图，是否是轴对称图形，若是，指出对称轴；(2)、∠ABC和∠ADC相等吗？为什么？(3)、判断BD是否被AC垂直平分，并说明你的理由．六、（本大题1个小题，共7分）
-
26. 如图，已知△ABC中，AB＝AC＝12厘米，BC＝9厘米，点D为AB的中点．
(1)、如果点P在线段BC上以3厘米/秒的速度由B向C点运动，同时点Q在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，1秒钟时，△BPD与△CQP是否全等，请说明；
②点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD≌△CPQ？
(2)、若点Q以②的运动速度从点C出发点P以原来运动速度从点B同时出发，都逆时针沿ABC的三边运动，求多长时间点P与点Q第一次在△ABC的哪条边上相遇？