福建省泉州市丰泽区2018-2019学年七年级下学期数学期末试卷
试卷更新日期：2020-06-12 类型：期末考试
一、选择题
-
1. 方程x﹣3＝5的解为（ ）A、x＝2 B、x＝﹣2 C、x＝8 D、x＝﹣82. 不等式﹣2x＞4的解集（ ）A、x＞2 B、x＞﹣2 C、x＜2 D、x＜﹣23. 如图所示的四个图案是我国几家国有银行的图标，其中图标属于中心对称的有（ ）
A、1个 B、2个 C、3个 D、4个4. 若a＜b，则下列不等式中正确的是（ ）A、 B、a﹣b＞0 C、a﹣2＜b﹣2 D、﹣3a＜﹣3b5. 一个三角形的两边分别是2和7，则它的第三边可能是（ ）A、3 B、4 C、5 D、66. 已知，在△ABC中，∠A＝45°，∠B＝46°，那么△ABC的形状为（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形7. 下列正多边形不能镶嵌成一个平面的是（ ）A、正三角形和正方形 B、正三角形和正六边形 C、正方形和正六边形 D、正方形和正八边形8. 如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，则∠1+∠2+∠3等于（ ）
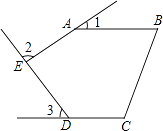A、90° B、180° C、210° D、270°9. 关于x的不等式组 的解集为x＜3，那么a的取值范围为（ ）A、a＝3 B、a＞3 C、a＜3 D、a≥310. 如图，△ABC≌△DEF，则此图中相等的线段有（ ）
A、1对 B、2对 C、3对 D、4对二、填空题
-
11. “x的3倍与2的差不大于7”列出不等式是 ．12. 若 是方程kx﹣y＝2的一组解，则k＝ ．13. 如图，在△ABC中，D是BC延长线上点，∠B＝50°，∠ACD＝110°，则∠A＝ ．
14. 一个多边形的每个内角都是150°，那么这个多边形的边数为 ．15. 若关于x的不等式x＜a恰有2个正整数解，则a的取值范围为 ．16. 如图，边长为3的等边△ABC与等边△DEF互相重合，将△ABC沿直线L向左平移m个单位长度，将△DEF向右也平移m个单位长度，如图，当C、E是线段BF的三等分点时m的值为 ．
三、解答题
-
17. ．18. 解不等式组 ，并把解集在数轴上表示出来．
19. 如图，△ABC的顶点都在方格纸的格点上．将△ABC向左平移2格，再向上平移4格．
(1)、请在图中画出平移后的三角形A′B′C′；(2)、若连接BB′，CC′，则这两条线段之间的关系是；(3)、在图中画出三角形A′B′C′的高C′D′．20. 我国明代数学家程大位的名著《算法统宗》里有一道著名算题，原文如下：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”．译文为：“有100个和尚分100个馒头，正好分完，如果大和尚一人分3个，小和尚3人分一个，试问大、小和尚各几人？”试用列方程（组）解应用题的方法求出问题的解．21. 如图，△ABC逆时针旋转一定角度后与△ADE重合，且点C在AD上．
(1)、指出旋转中心；(2)、若∠B＝21°，∠ACB＝26°，求出旋转的度数；(3)、岩AB＝5，CD＝3，则AE的长是多少？为什么？22. 已知关于x，y的方程组(1)、当x＝1时，求y的值；(2)、若x＞y，求k的取值范围．23. 如图，直线l与m分别是△ABC边AC和BC的垂直平分线，l与m分别交边AB，BC于点D和点E．
(1)、若AB＝10，则△CDE的周长是多少？为什么？(2)、若∠ACB＝125°，求∠DCE的度数．24. 某市举办中学生“梦想杯”足球联赛，联赛记分办法是：胜场得3分，平1场得I分，负1场得0分．复兴中学足球队参加了18场比赛，积24分．(1)、在这次足球联赛中，如果复兴中学足球队踢平场数与所负场数相同，那么它胜了几场？(2)、在这次足球联赛中，如果复兴中学足球队踢平场数多于所负场数，那么它的胜、平、负情况共有多少种？25. 如图1，线段AB、CD相交于点O，连接AD、CB．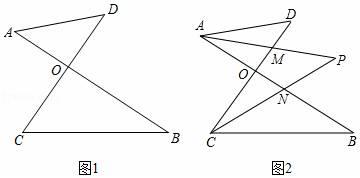
(1)、请说明：∠A+∠D＝∠B+∠C；(2)、点M在OD上，点N在OB上，AM与CN相交于点P，且∠DAP＝ ∠DAB．∠DCP＝ ∠DCB，其中n为大于1的自然数（如图2）．①当n＝2时，试探索∠P与∠D、∠B之间的数量关系，并请说明理由；
②对于大于1的任意自然数n，∠P与∠D、∠B之间存在着怎样的数量关系？请直接写出你的探索结果，不必说明理由．