福建省南平市2018-2019学年七年级下学期数学期末试卷

试卷更新日期：2020-06-12 类型：期末考试

进入出卷网下载

一、选择题

1. 下列四个数中，属于无理数的是（　　）

A、 $\frac{2}{3}$ B、0.5 C、2 D、π

查看试题解析
2. 下列调查中，不适合用全面调查的是（　　）

A、了解全班学生的课外读书时间 B、旅客上飞机前的安检 C、学校招聘教师，对应聘人员的面试 D、了解一批灯管的使用寿命

查看试题解析
3. 下列命题属于真命题的是（　　）

A、如果a＜0，b＞0，那么a+b＜0 B、相等的两个角一定是对顶角 C、同角的补角相等 D、如果两条直线被第三条直线所截，那么同位角相等

查看试题解析
4. 不等式组 ${\begin{cases} x > - 2 \\ x < 1 \end{cases}$ 的整数解个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
5. 已知点P在第四象限，它到x轴的距离为6，到y轴的距离为5，则点P的坐标为（　　）

A、（6，﹣5） B、（5，﹣6） C、（﹣6，5） D、（﹣5，6）

查看试题解析
6. 如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1＝35°，则∠2等于（　　）

A、35° B、45° C、55° D、65°

查看试题解析
7. 我国民间流传着这样一道题：只闻隔壁人分银，不知多少银和人；每人7两多7两，每人半斤少半斤，试问各位善算者，多少人分多少银（注：古代1斤＝16两）．设有x人，分y两银，则（　　）

A、 ${\begin{cases} 7 x = y - 7 \\ 8 x = y + 8 \end{cases}$ B、 ${\begin{cases} 7 x = y - 7 \\ 5 x = y + 5 \end{cases}$ C、 ${\begin{cases} y = 7 x - 7 \\ y = 8 x + 8 \end{cases}$ D、 ${\begin{cases} y = 7 x + 7 \\ y = 5 x - 5 \end{cases}$

查看试题解析
8. 在平面直角坐标系中，点A，B，C，D，E，F的位置如图所示，如果点E的坐标是（﹣3，0），点F的坐标是（3，0），则在第三象限上的点是（　　）

A、点A B、点B C、点C D、点D

查看试题解析
9. 如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）

A、∠D＝∠A B、∠1＝∠2 C、∠3＝∠4 D、∠D＝∠DCE

查看试题解析
10. 在平面直角坐标系中，长方形ABCD的边BC平行于x轴，如果点A的坐标为（﹣1，2），点C的坐标为（3，﹣3），把一条长为2019个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按如图所示的逆时针方向绕在长方形ABCD的边上，则细线的另一端所在位置的点的坐标是（　　）

A、（﹣1，1） B、（﹣1，﹣1） C、（2，﹣2） D、（2，2）

查看试题解析

二、填空题

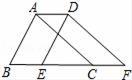
11. 4是的算术平方根．

查看试题解析
12. 样本容量为90的数据中，最大值是133，最小值是40，取组距为10，则可以分成组．

查看试题解析
13. 如图，将周长为8的三角形ABC向右平移1个单位后得到三角形DEF，则四边形ABFD的周长等于．

查看试题解析
14. 若x^2m^﹣1﹣2yⁿ^﹣1＝3是关于x，y的二元一次方程，则（m﹣n）²⁰¹⁹＝．

查看试题解析
15. 若点P（2m﹣1，m﹣3）在第一象限，则m的取值范围是．

查看试题解析
16. 如图所示为一个按某种规律排列的数阵：

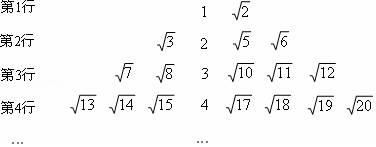
根据数阵的规律，第7行倒数第二个数是．

查看试题解析

三、解答题

17. 计算： $\sqrt{{(- 2)}^{2}} + {}^{3}{\sqrt{27}} - | \sqrt{3} - 2 | - \sqrt{3}$ ．

查看试题解析
18. 解不等式组： ${\begin{cases} 6 x - 1 < 5 x + 2 ① \\ \frac{x - 5}{2} > 2 x - 1 ② \end{cases}$

查看试题解析
19. 如图，在平面直角坐标系中，点A（0，﹣1），B（﹣3，﹣3），C（1，﹣3），将三角形ABC平移，使点A的对应点A'的坐标为（2，3）．

(1)、画出平移后的三角形A'B'C'；

(2)、点B'的坐标是．

查看试题解析
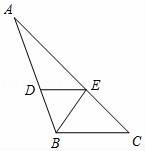
20. 阅读下面解答过程，并填空或在括号内填写理由．
已知BE平分∠ABC交AC于点E，DE∥BC，且∠ABC＝110°，∠C＝35°，

请说明BE⊥AC．

解：∵BE平分∠ABC（已知），

∴∠EBC＝ $\frac{1}{2}$ ∠（角平分线定义）．

∵∠ABC＝110°，

∴∠EBC＝°．

∵DE∥BC，∠C＝35°（已知），

∴∠EBC＝∠（两直线平行，内错角相等），

∠C＝∠AED＝35°（）．

∴∠AEB＝∠+∠＝90°．

∴BE⊥AC．

查看试题解析
21. 列方程解应用题：丰收村2台大收割机和5台小收割机同时工作2h共收割小麦3.6hm²；3台大收割机和2台小收割机同时工作5h共收割小麦8hm².1台大收割机和1台小收割机每小时各收割小麦多少公顷？

查看试题解析

22. 某学校随机抽取部分学生，调查每个月的零花钱消费额，数据整理成如下的统计表和如图①②所示的两幅不完整的统计图，已知图①中A，E两组对应的小长方形的高度之比为2：1．请结合相关数据解答以下问题：月消费额分组统计表

组别	月零花钱消费额/元
A	10≤x＜100
B	100≤x＜200
C	200≤x＜300
D	300≤x＜400
E	x≥400

(1)、本次调查样本的容量是；

(2)、补全频数分布直方图，并标明各组的频数；

(3)、若该学校有2500名学生，请估计月消费零花钱不少于300元的学生的数量．

查看试题解析

23. 如图，在平面直角坐标系中，已知点A的坐标是（a，0），点B的坐标是（b，0），其中a，b满足 $\sqrt{a + 1}$ + ${(b - 3)}^{2}$ ＝0．

(1)、填空：a＝， b＝；

(2)、在y轴负半轴上有一点M（0，m），三角形ABM的面积为4．
①求m的值；

②将线段AM沿x轴正方向平移，使得A的对应点为B，M的对应点为N．若点P为线段AB上的任意一点（不与A，B重合），试写出∠MPN，∠PMA，∠PNB之间的数量关系，并说明理由．

查看试题解析