江西省宜春市丰城市2018-2019学年七年级下学期数学期末试卷

试卷更新日期：2020-06-12 类型：期末考试

进入 出卷网 下载

一、选择题

  • 1. 16的算术平方根是（   ）
    A、  ±4 B、±2 C、4 D、－4

    查看试题解析

  • 2. 下列调查活动中适合使用全面调查的是（　　）
    A、某种品牌插座的使用寿命 B、全国植树节中栽植树苗的成活率 C、了解某班同学课外阅读经典情况 D、调查“厉害了，我的国”大型记录电影在线收视率

    查看试题解析

  • 3. 下列不等式中，变形错误的是（　　）
    A、若a＞b，则b＜a B、若a＞b，则a+c＞b+c C、若ac2＞bc2，则a＞b D、若-x＞a，则x＞-a

    查看试题解析

  • 4. 将点A先向下平移3个单位长度，再向右平移4个单位长度，得到点A'（-3，-6），则点A的坐标为（　　）
    A、（-7，3） B、（6，-10） C、（-7，-3） D、（-1，-10）

    查看试题解析

  • 5. 把一副三角板放在同一水平桌面上，摆放成如图所示的形状，使两个直角顶点重合，两条斜边平行，则∠1的度数是（  ）

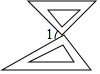    A、45° B、60° C、75° D、82.5°

    查看试题解析

  • 6. 关于x、y的二元一次方程组 {x+3y=2+a3x+y=−4a 的解满足x+y＞2，则a的取值范围为（　　）
    A、a＜-2 B、a＞-2 C、a＜2 D、a＞2

    查看试题解析

二、填空题

  • 7. 一个正数的平方根分别是x+1和x-5，则x=

    查看试题解析

  • 8. 已知平面直角坐标系中的点P（a-3，2）在第二象限，则a的取值范围是

    查看试题解析

  • 9. 为了解某校七年级500名学生的身高情况，从中抽取了100名学生进行测量，其中有30名学生的身高在165cm以上，则该问题中的样本容量是 ．

    查看试题解析

  • 10. 《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问：牛、羊各直金几何？”

    译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问：每头牛、每只羊各值金多少两？”设每头牛值金x两，每只羊值金y两，可列方程组为 ．

    查看试题解析

  • 11. 若不等式组 {x+1>02x−a<0 的最大正整数解是3，则a的取值范围是

    查看试题解析

  • 12. 将一副三角板按如图放置，小明得到下列结论：①如果∠2=30°，则有AC∥DE；②∠BAE+∠CAD=180°；③如果BC∥AD，则有∠2=30°；④如果∠CAD=150°，则∠4=∠C；那么其中正确的结论有

    ．

    查看试题解析

三、（本大题共五个小题，每小题6分，共30分）

  • 13.    
    (1)、计算： 83−5−|3−2|+25  
    (2)、解方程组： {2x−y=03x−2y=5  

    查看试题解析

  • 14. 已知 2a-1的算术平方根是3，3a+b+4的立方根是2，求3a+b的平方根.

    查看试题解析

  • 15. 如图，直线AB、CD相交于点O，OE平分∠BOD，

    (1)、若∠AOC=70°，求∠BOE的度数；
    (2)、若OF平分∠AOD，试说明OE⊥OF．

    查看试题解析

  • 16. 解不等式组： {x−3(x−1)<7x−2⩽2x−33  

    查看试题解析

  • 17. 已知关于x，y的二元一次方程组 {2x−y=4m−5x+4y=−7m+2 的解满足x+y＞-3，其中m是非负整数，求m的值．

    查看试题解析

四、（本大题共三个小题，每小题8分，共24分）

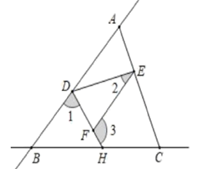
  • 18. 如图，直线AB和直线BC相交于点B，连接AC，点D.E.H分别在AB、AC、BC上，连接DE、DH，F是DH上一点，已知∠1+∠3=180°，

    (1)、求证：∠CEF=∠EAD；
    (2)、若DH平分∠BDE，∠2=α，求∠3的度数.(用α表示).

    查看试题解析

  • 19. 已知关于x，y的方程组 {x+y=−3a+9x−y=−5a+1 的解为正数．
    (1)、求a的取值范围；
    (2)、化简|-4a+5|-|a+4|．

    查看试题解析

  • 20.

    为了促进学生多样化发展，某校组织开展了社团活动，分别设置了体育类、艺术类、文学类及其它类社团（要求人人参与社团，每人只能选择一项）．为了解学生喜爱哪种社团活动，学校做了一次抽样调查．根据收集到的数据，绘制成如下两幅不完整的统计图，请根据图中提供的信息，完成下列问题：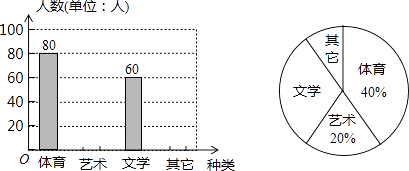

    (1)、此次共调查了多少人？

    (2)、求文学社团在扇形统计图中所占圆心角的度数；

    (3)、请将条形统计图补充完整；

    (4)、若该校有1500名学生，请估计喜欢体育类社团的学生有多少人？

    查看试题解析

五、（本大题共两个小题，每小题9分，共18分）

  • 21. 如图，平面直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）．

    (1)、写出点A、B的坐标：A ， B；
    (2)、将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A1B1C1 ， 画出△A1B1C1；
    (3)、若AB边上有一点M（a，b），平移后对应的点M1的坐标为；
    (4)、求△ABC的面积．

    查看试题解析

  • 22. 某商场销售A，B两种品牌的多媒体教学设备，这两种多媒体教学设备的进价和售价如表所示

    A

    B

    进价（万元/套）

    2

    1.6

    售价（万元/套）

    2.6

    2
    (1)、若该商场计划购进两种多媒体教学设备若干套，共需124万元，全部销售后可获毛利润36万元．则该商场计划购进A，B两种品牌的多媒体教学设备各多少套？
    (2)、通过市场调研，该商场决定在（1）中所购总数量不变的基础上，减少A种设备的购进数量，增加B种设备的购进数量．若用于购进这两种多媒体教学设备的总资金不超过120万元，且全部销售后可获毛利润不少于33.6万元．问有几种购买方案？并写出购买方案．

    查看试题解析

六、（本大题共12分）

  • 23. 某学习小组发现一个结论：已知直线a∥b，若直线c∥a，则c∥b．他们发现这个结论运用很广，请你利用这个结论解决以下问题：

    已知直线AB∥CD，点E在AB、CD之间，点P、Q分别在直线AB、CD上，连接PE、EQ．

    (1)、如图1，运用上述结论，探究∠PEQ与∠APE+∠CQE之间的数量关系，并说明理由；
    (2)、如图2，PF平分∠BPE，QF平分∠EQD，当∠PEQ=140°时，求出∠PFQ的度数；
    (3)、如图3，若点E在CD的下方，PF平分∠BPE，QH平分∠EQD，QH的反向延长线交PF于点F．当∠PEQ=70°时，请求出∠PFQ的度数．

    查看试题解析