江西省新余市2018-2019学年七年级下学期数学期末试卷
试卷更新日期:2020-06-12 类型:期末考试
一、选择题
-
1. 下列实数是无理数的是( )
A、-2 B、0 C、 D、2. 要反映武汉市某月每天的最低气温的变化趋势,宜采用( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布统计图3. 已知a>b,c≠0,则下列关系一定成立的是( )A、ac>bc B、 C、c-a>c-b D、c+a>c+b4.如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,则∠1+∠2等于( )
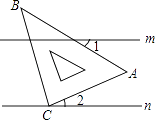 A、30° B、40° C、45° D、60°5. 若方程mx-2y=3x+4是关于x,y的二元一次方程,则m满足( )A、m≠-2 B、m≠0 C、m≠3 D、m≠46. 若不等式组 有解,则a的取值范围是( )A、a≤3 B、a<3 C、a<2 D、a≤2
A、30° B、40° C、45° D、60°5. 若方程mx-2y=3x+4是关于x,y的二元一次方程,则m满足( )A、m≠-2 B、m≠0 C、m≠3 D、m≠46. 若不等式组 有解,则a的取值范围是( )A、a≤3 B、a<3 C、a<2 D、a≤2二、填空题
-
7. 16的算术平方根是8. 点P(2,m)在x轴上,则B(m-1,m+1)在第象限.9. “十一”黄金周,国光超市“女装部”推出“全部服装八折”,男装部推出“全部服装八五折”的优惠活动,某顾客在女装部购买了原价为x元,男装部购买了原价为y元的服装各一套,优惠前需付700元,而他实际付款580元,则可列方程组为 .10. 有100个数据,其中最大值为76,最小值为28,若取组距为5,对数据进行分组,则应分为组.11. 对于平面直角坐标系xOy中的点P(a,b),若点P的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P为点P的“k属派生点”,例如:P(1,4)的“2属派生点”为P(1+2×4,2×1+4),即P′(9,6).若点P在x轴的正半轴上,点P的“k属派生点”为点P′,且线段PP′的长度为线段OP长度的5倍,则k的值为12. 一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺至少有一组边互相平行.如图2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为

三、(本大题共5小题,每小题6分,共30分)
-
13.(1)、计算: ;(2)、已知(x-1)2=4,求x的值.14. 解方程组 .15. 已知2a-1的平方根是±3,3a+b-9的立方根是2,c是 的整数部分.求a+2b+c的算术平方根.16. 解不等式组 ,并将解集在数轴上表示出来.17. 如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
 (1)、求∠AON的度数.(2)、写出∠DON的余角.
(1)、求∠AON的度数.(2)、写出∠DON的余角.四、(本大题共3小题,每小题8分,共24分)
-
18. 若关于x、y的二元一次方程组 的解满足x+y>- ,求出满足条件的m的所有正整数值.19. 如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1.求证:AD平分∠BAC.
 20. 如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
20. 如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题: (1)、请在图中建立适当的直角坐标系,并写出图书馆(B)位置的坐标;(2)、若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
(1)、请在图中建立适当的直角坐标系,并写出图书馆(B)位置的坐标;(2)、若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.五、(本大题共2小题,每小题9分,共18分)
-
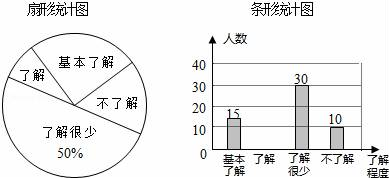
21. “校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
 (1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为度;(2)、请补全条形统计图;(3)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.22. 湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.(1)、求温馨提示牌和垃圾箱的单价各是多少元?(2)、该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
(1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为度;(2)、请补全条形统计图;(3)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.22. 湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.(1)、求温馨提示牌和垃圾箱的单价各是多少元?(2)、该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?六、(本大题共12分)
-
23. 在直角坐标系中,已知点A(a,0),B(b,c),C(d,0),a是-8的立方根,方程2x3b-5-3y2b-2c+5=1是关于x,y的二元一次方程,d为不等式组 的最大整数解.
 (1)、求点A、B、C的坐标;(2)、如图1,若D为y轴负半轴上的一个动点,当AD∥BC时,∠ADO与∠BCA的平分线交于M点,求∠M的度数;(3)、如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使S△ADE≤S△BCE?若存在,请求出D的纵坐标yD的取值范围;若不存在,请说明理由.
(1)、求点A、B、C的坐标;(2)、如图1,若D为y轴负半轴上的一个动点,当AD∥BC时,∠ADO与∠BCA的平分线交于M点,求∠M的度数;(3)、如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使S△ADE≤S△BCE?若存在,请求出D的纵坐标yD的取值范围;若不存在,请说明理由.