江西省吉安市永新县、泰和县2018-2019学年七年级下学期数学期末试卷

试卷更新日期：2020-06-12 类型：期末考试

进入 出卷网 下载

一、选择题

  • 1. 北京春夏之季鲜花烂漫，空气中弥漫着各种花粉，有一种花粉的直径是0.000063米，将0.000063用科学记数法表示应为（　　）
    A、6.3×10﹣4 B、0.63×10﹣4 C、6.3×10﹣5 D、63×10﹣5

    查看试题解析

  • 2. 下列计算正确的是（　　）
    A、a5+a2＝a7 B、2a2﹣a2＝2 C、a3•a2＝a6 D、（a2）3＝a6

    查看试题解析

  • 3. 如图，直线c与直线a，b相交，且a∥b，∠1＝60°，则∠2的度数是（　　）

    A、30° B、60° C、120° D、80°

    查看试题解析

  • 4. 事件：“在只装有3个红球和4个黑球的袋子里，摸出一个白球”是（　　）
    A、可能事件 B、不可能事件 C、随机事件 D、必然条件

    查看试题解析

  • 5. 下列各数：3 5 ， 25 ，3.141414…， 103 ，0.1010010001…（两个1之间依次增加一个0）， 0.0273 ，﹣5， 13 ，是无理数的有（　　）个
    A、3个 B、4个 C、5个 D、6个

    查看试题解析

  • 6. 长度分别为3cm，5cm，7cm，9cm的四根木棒，能搭成（首尾连结）三角形的个数为（　　）

    A、1 B、2 C、3 D、4

    查看试题解析

  • 7. 下列图形中，不一定是轴对称图形的是（    ）

    A、等腰三角形 B、线段 C、钝角 D、直角三角形

    查看试题解析

  • 8. 如图，AB⊥BC，DC⊥BC，AE平分∠BAD，DE平分∠ADC，以下结论，其中正确的是（　　）

    ①∠AED＝90°；

    ②点E是BC的中点；

    ③DE＝BE；

    ④AD＝AB+CD．

    A、①②③ B、①②④ C、①③④ D、②③④

    查看试题解析

二、填空题

  • 9. 计算4a2b÷2ab＝；

    查看试题解析

  • 10. 等腰三角形一边长是10cm，一边长是6cm，则它的周长是cm或cm．

    查看试题解析

  • 11. 如图所示，A、B、C、D在同一直线上，AB＝CD，DE∥AF，若要使△ACF≌△DBE，则还需要补充一个条件： ．

    查看试题解析

  • 12. 若式子x2+4x+m2是一个含x的完全平方式，则m＝ ．

    查看试题解析

  • 13. 一棵树高h（m）与生长时间n（年）之间有一定关系，请你根据下表中数据，写出h（m）与n（年）之间的关系式： ．

    n/年

    2

    4

    6

    8

    …

    h/m

    2.6

    3.2

    3.8

    4.4

    …

    查看试题解析

  • 14. 把一根长度为6的铁丝截成3段，若三段的长度均为正整数，则能构成三角形的概率 ．

    查看试题解析

  • 15. 若a+b＝3，ab＝2，则a2+b2＝ ．

    查看试题解析

  • 16.

    如图，△ABC中，AD是高，AE是∠BAC的平分线，∠B＝70°，∠DAE＝18°，则∠C的度数是。

    查看试题解析

  • 17. 点A（3，﹣5）向上平移4个单位，再向左平移3个单位到点B，则点B的坐标为 ．

    查看试题解析

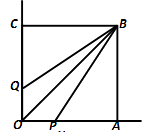
  • 18.

    如图，正方形OABC的边长为3，点P与点Q分别在射线OA与射线OC上，且满足BP＝BQ，若AP＝2，则四边形OPBQ面积的值可能为 ．

    查看试题解析

三、解答题

  • 19. 计算：
    (1)、﹣12﹣（1﹣0.5） ÷52×15 ；
    (2)、9.7×10.3（利用平方差公式计算）．

    查看试题解析

  • 20. 先化简，再求值：[（x﹣y）2+（x+y）（x﹣y）]÷2x，其中x＝﹣1，y＝2．

    查看试题解析

  • 21. 一个角的余角比它补角的 14 还少12℃，求这个角的度数．

    查看试题解析

四、（本大题共两小题，每小题8分，共16分）

  • 22. 如图是甲、乙两人从同一地点出发后，路程随时间变化的图象.

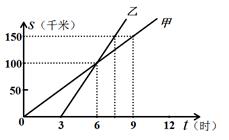    (1)、此变化过程中， 是自变量， 是因变量.
    (2)、甲的速度 乙的速度.（填“大于”、“等于”、或“小于”）
    (3)、甲与乙 时相遇.
    (4)、甲比乙先走 小时.
    (5)、9时甲在乙的 （填“前面”、“后面”、“相同位置”）.
    (6)、路程为150km，甲行驶了 小时，乙行驶了 小时.

    查看试题解析

  • 23. 如图，方格纸中每个小正方形的边长均为1，四边形ABCD的四个顶点都在小正方形的顶点上，点E在BC边上，且点E在小正方形的顶点上，连接AE．

    (1)、在图中画出△AEF，使△AEF与△AEB关于直线AE对称，点F与点B是对称点；
    (2)、请写出△AEF与四边形ABCD重叠部分的面积．

    查看试题解析

五、（本大题共两小题，每小题9分，共18分）

  • 24. 如图，在四边形ABCD中，AB∥CD，∠1＝∠2，DB＝DC．

    (1)、求证：△ABD≌△EDC；
    (2)、若∠A＝135°，∠BDC＝30°，求∠BCE的度数．

    查看试题解析

  • 25. 在一个不透明的袋子中装有4个红球和6个黄球，这些球除颜色外都相同，将袋子中的球充分摇匀后，随机摸出一球．
    (1)、分别求摸出红球和摸出黄球的概率．
    (2)、为了使摸出两种球的概率相同，再放进去8个同样的红球或黄球，那么这8个球中红球和黄球的数量分别是多少？

    查看试题解析

六、（本大题共1小题，共12分）

  • 26. 如图，在△ABC中，已知AB＝AC，∠BAC＝90°，AH是△ABC的高，AH＝4 cm，BC＝8 cm，直线CM⊥BC，动点D从点C开始沿射线CB方向以每秒3厘米的速度运动，动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动，连接AD、AE，设运动时间为t（t＞0）秒．

    (1)、请直接写出CD、CE的长度（用含有t的代数式表示）：CD＝cm，CE＝cm；
    (2)、当t为多少时，△ABD的面积为12cm2？
    (3)、请利用备用图探究，当t为多少时，△ABD≌△ACE？并简要说明理由．

    查看试题解析