江西省赣州市2018-2019学年七年级下学期数学期末试卷

试卷更新日期：2020-06-12 类型：期末考试

进入 出卷网 下载

一、选择题

  • 1. 下列各数中最小的是（　　）

    A、0 B、﹣3 C、﹣ 3 D、1

    查看试题解析

  • 2. 如图所示，AB∥CD ， EF⊥BD ， 垂足为E ， ∠1＝50°，则∠2的度数为（　　）

    A、50° B、40° C、45° D、25°

    查看试题解析

  • 3. 在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 4. 9的算术平方根是(   )

    A、3 B、±3 C、3 D、±3

    查看试题解析

  • 5. 小美将某服饰店的促销活动内容告诉小明后，小明假设某一商品的定价为x元，并列出关系式为0.3（2x﹣100）＜1000，则下列何者可能是小美告诉小明的内容？（   ）
    A、买两件等值的商品可减100元，再打3折，最后不到1000元 B、买两件等值的商品可减100元，再打7折，最后不到1000元 C、买两件等值的商品可打3折，再减100元，最后不到1000元 D、买两件等值的商品可打7折，再减100元，最后不到1000元

    查看试题解析

  • 6.

    如图，直线m⊥n，在某平面直角坐标系中，x轴∥m，y轴∥n，点A的坐标为（﹣4，2），点B的坐标为（2，﹣4），则坐标原点为（　　）

    A、O1 B、O2 C、O3 D、O4

    查看试题解析

二、填空题

  • 7. 与﹣ 3 最接近的整数是 ．

    查看试题解析

  • 8. 如图，乐乐用剪刀沿直线将一片平整的树叶减掉一部分，发现剩下树叶的周长比原周长小，能正确解释这一现象的数学依据是 ．

    查看试题解析

  • 9. 不等式组 {3x+6≥04−2x>0 的所有整数解的和为 .

    查看试题解析

  • 10.

    如图，下面每个图形中的四个数都是按相同的规律填写的，根据此规律确定x的值为 ．


    查看试题解析

  • 11. 如图，将一条长为7cm的卷尺铺平后折叠，使得卷尺自身的一部分重合，然后在重合部分（阴影处）沿与卷尺边垂直的方向剪一刀，此时卷尺被分成了三段，若这三段长度由短到长之比为1：2：4，其中没完全盖住的部分最长，则折痕对应的刻度可能是cm

    查看试题解析

三、（本大题共5小题，每小题6分，共30分）

  • 12.      
    (1)、计算：| 5 ﹣4|﹣ 16 +2 5
    (2)、解方程的 {x+2y=5x+y=3

    查看试题解析

  • 13. 解不等式组 {2x+3>3xx+33−x−16≥12 ，并把解集在数轴上表示出来．

    查看试题解析

  • 14. 如图，完成下面的推理：∵∠A＝75°，∠1＝75°（已知）

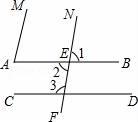
    ∴∠A＝∠1

    ∴∥（）

    ∠2＝∠1（对顶角相等

    ∠3＝105°（已知），∴+∠3＝180°

    ∴AB∥CD

    查看试题解析

  • 15. 如图，在△ABC和△DCB中，∠A＝∠D＝90°，AC＝BD ， AC与BD相交于点O ， 限用无刻度直尺完成以下作图：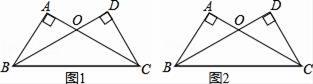

    (1)、在图1中作线段BC的中点P；
    (2)、在图2中，在OB、OC上分别取点E、F ， 使EF∥BC ．

    查看试题解析

  • 16. 在如图所示的方格图中，我们称每个小正方形的顶点为“格点”，以格点为顶点的三角形叫做“格点三角形”，根据图形，回答下列问题．

    (1)、图中格点△A′B′C′是由格点△ABC通过怎样的变换得到的？
    (2)、如果以直线a、b为坐标轴建立平面直角坐标系后，点A的坐标为（﹣3，4），请写出格点△DEF各顶点的坐标，并求出△DEF的面积．

    查看试题解析

四、（本大题共3小题，每小题8分，共24分）

  • 17. 已知点M（3a﹣2，a+6），分别根据下列条件求出点M的坐标．
    (1)、点M在x轴上；
    (2)、点N的坐标为（2，5），且直线MN∥x轴；
    (3)、点M到x轴、y轴的距离相等．

    查看试题解析

  • 18. 如图，一只蚂蚁从点A沿数轴向右爬2 2 个单位后到达点B ， 点A表示﹣2，设点B所表示的数为m ．

    (1)、求m的值；
    (2)、求|m﹣3 2 |+ (m−2)2 的值．

    查看试题解析

  • 19. 某兴趣小组为了了解本校男生参加课外体育锻炼情况，随机抽取本校300名男生进行了问卷调查，统计整理并绘制了如下两幅尚不完整的统计图．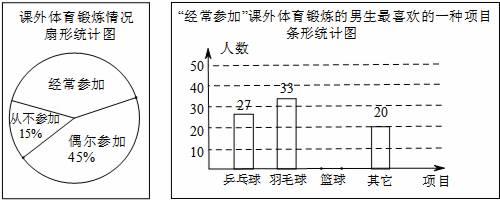

    请根据以上信息解答下列问题：

    (1)、课外体育锻炼情况扇形统计图中，“经常参加”所对应的圆心角的度数为；
    (2)、请补全条形统计图；
    (3)、该校共有1200名男生，请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数；
    (4)、小明认为“全校所有男生中，课外最喜欢参加的运动项目是乒乓球的人数约为1200× 27300 ＝108”，请你判断这种说法是否正确，并说明理由．

    查看试题解析

五、（本大题共2小题，每小题9分，共18分）

  • 20. 如图1，已知AB∥CD ， ∠B＝20°，∠D＝110°．

    (1)、若∠E＝50°，请求出∠F的度数；
    (2)、探索∠E与∠F之间满足的数量关系，并说明理由；
    (3)、如图2，EP平分∠BEF ， FG平分∠EFD ， FG的反向延长线交EP于点P ， 求∠P的度数．

    查看试题解析

  • 21. 某数学兴趣小组研究我国古代《算法统宗》里这样一首诗：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．诗中后两句的意思是：如果每一间客房住7人，那么有7人无房可住；如果每一间客房住9人，那么就空出一间房．
    (1)、求该店有客房多少间？房客多少人？
    (2)、假设店主李三公将客房进行改造后，房间数大大增加．每间客房收费20钱，且每间客房最多入住4人，一次性订客房18间以上（含18间），房费按8折优惠．若诗中“众客”再次一起入住，他们如何订房更合算？

    查看试题解析

六、（本大题共1小题，共12分）

  • 22. 如图，在平面直角坐标系中，点A ， B的坐标分别为A（0，a），B（b ， a），且a ， b满足（a﹣3）2+|b﹣6|＝0，现同时将点A ， B分别向下平移3个单位，再向左平移2个单位，分别得到点A ， B的对应点C ， D ， 连接AC ， BD ， AB ．

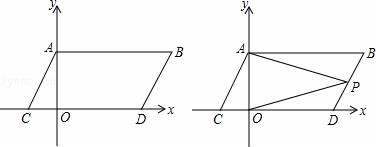    (1)、求点C ， D的坐标及四边形ABDC的面积S四边形ABCD；
    (2)、在y轴上是否存在一点M ， 连接MC ， MD ， 使S△MCD＝ 1 3 S四边形ABCD？若存在这样一点，求出点M的坐标，若不存在，试说明理由；
    (3)、点P是直线BD上的一个动点，连接PA ， PO ， 当点P在BD上移动时（不与B ， D重合），直接写出∠BAP ， ∠DOP ， ∠APO之间满足的数量关系．

    查看试题解析