福建省漳州市2018-2019学年七年级下学期数学期末试卷
试卷更新日期:2020-06-12 类型:期末考试
一、选择题
-
1. 45°的余角是A、45° B、90° C、135° D、180°2. 在下列图形中, 与 是对顶角的是A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是A、 B、 C、 D、4. 下面四幅“二十四节气”标识系统设计分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是A、
3. 下列运算正确的是A、 B、 C、 D、4. 下面四幅“二十四节气”标识系统设计分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是A、 B、
B、 C、
C、 D、
D、 5. 如图,转盘被分成8个相同的扇形,自由转动转盘,当转盘停止时,指针落在阴影部分区域的概率是
5. 如图,转盘被分成8个相同的扇形,自由转动转盘,当转盘停止时,指针落在阴影部分区域的概率是 A、 B、 C、 D、6. 等腰三角形的周长为22,其中一边长是8,则其余两边长分别是A、6和8 B、7和8 C、7和7 D、6,8或7,77. 如图,已知 ,要说明 ,还需从下列条件① ,② ,③ ,④ 中选一个,则正确的选法个数是
A、 B、 C、 D、6. 等腰三角形的周长为22,其中一边长是8,则其余两边长分别是A、6和8 B、7和8 C、7和7 D、6,8或7,77. 如图,已知 ,要说明 ,还需从下列条件① ,② ,③ ,④ 中选一个,则正确的选法个数是 A、1个 B、2个 C、3个 D、4个8. 甲、乙两人在100米赛跑中,路程 与时间 的关系如图所示,根据图象,下列结论错误的是
A、1个 B、2个 C、3个 D、4个8. 甲、乙两人在100米赛跑中,路程 与时间 的关系如图所示,根据图象,下列结论错误的是 A、甲比乙先到达终点 B、甲、乙速度相差 C、甲的速度为 D、乙跑完全程需9. 如图, 中, 平分 , 垂直平分 交 于点 ,交 于点 ,连接 ,若 , ,则 的度数为
A、甲比乙先到达终点 B、甲、乙速度相差 C、甲的速度为 D、乙跑完全程需9. 如图, 中, 平分 , 垂直平分 交 于点 ,交 于点 ,连接 ,若 , ,则 的度数为 A、 B、 C、 D、10. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A、 B、 C、 D、10. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是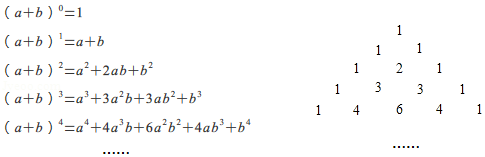 A、2016 B、2017 C、2018 D、2019
A、2016 B、2017 C、2018 D、2019二、填空题
-
11. 流感病毒的直径为0.00000008m,用科学记数法表示为m.12. 写出一个不可能事件 .13. 一不透明的口袋里装有白球和红球共20个,这些球除颜色外完全相同,小明通过多次模拟试验后发现,其中摸到白色球的频率稳定在0.2左右,则口袋中红色球可能有个.14. 若 , ,则 的值是 .15. 如图,把一个直角三角尺 的直角顶点放在长方形桌面 的顶点 处,桌面的另一个顶点 在三角尺斜边上.若 ,则 .
 16. 如图, 中, , , , ,点 、 分别在边 和射线 上运动,若 与 全等,则 的长是 .
16. 如图, 中, , , , ,点 、 分别在边 和射线 上运动,若 与 全等,则 的长是 .
三、解答题
-
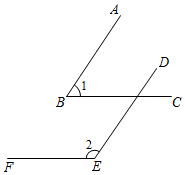
17. 计算:18. 先化简,再求值: ,其中 , .19. 如图, , ,试说明: .
 20. 如图,已知 ,求作射线 ,使 (要求:尺规作图,保留作图痕迹,不写作法),并说明其中的道理.
20. 如图,已知 ,求作射线 ,使 (要求:尺规作图,保留作图痕迹,不写作法),并说明其中的道理. 21. 航拍无人机甲从海拔 处出发,以 匀速铅直上升,与此同时,航拍无人机乙从海拔 处出发,以 匀速铅直上升.设无人机上升时间为 ,无人机甲、乙所在位置的高度分别为 、(1)、根据题意,填写下表:
21. 航拍无人机甲从海拔 处出发,以 匀速铅直上升,与此同时,航拍无人机乙从海拔 处出发,以 匀速铅直上升.设无人机上升时间为 ,无人机甲、乙所在位置的高度分别为 、(1)、根据题意,填写下表:上升时间
5
10
25
60
(2)、请你分别写出 、 与 的关系式;(3)、在某时刻两架无人机能否位于同一高度?若能,求无人机上升的时间和所在高度;若不能,请说明理由.22. 一个袋中装有7个红球,8个黑球,9个白球,每个球除颜色外都相同.(1)、求从袋中随机摸出一个球是红球的概率;(2)、若先从袋中拿出7个红球和 个黑球,再从剩下的球中摸出一球.①若事件“再摸出的球是白球”为必然事件,求 的值;
②若事件“再摸出的球是白球”为随机事件,求 的值,并求出这个事件概率的最小值.
23.(1)、如图1,边长为 的大正方形中有一个边长为 的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).通过观察比较图2与图1中的阴影部分面积,可以得到乘法公式 . (用含 , 的等式表示) (2)、运用(1)中所得到的公式,计算下列各题:
(2)、运用(1)中所得到的公式,计算下列各题:①
②
24. 如图,四边形 中, ,点 在 边上, 平分 , 平分 . (1)、按三角形内角的大小分类,试判断 的形状,并说明理由;(2)、若 , ,求点 到 的距离.25. 在 中,点 在 边所在直线上(与点 , 不重合),点 在 边所在直线上,且 , 交 边于点 .
(1)、按三角形内角的大小分类,试判断 的形状,并说明理由;(2)、若 , ,求点 到 的距离.25. 在 中,点 在 边所在直线上(与点 , 不重合),点 在 边所在直线上,且 , 交 边于点 . (1)、如图1,若 是等边三角形,点 在 边上,过点 作 于 ,试说明: .
(1)、如图1,若 是等边三角形,点 在 边上,过点 作 于 ,试说明: .某同学发现可以由以下两种思路解决此问题:
思路一:过点 作 ,交 于点 ,如图1
因为 是等边三角形,得 是等边三角形
又由 ,得
再说明
得出 .
从而得到结论.
思路二:过点 作 ,交 的延长线于点 ,如图
①请你在“思路一”中的括号内填写理由;
②根据“思路二”的提示,完整写出说明过程;
(2)、如图3,若 是等腰直角三角形, ,点 在线段 的延长线上,过点 作 于 ,试探究 与 之间的数量关系,并说明理由.