福建省三明市县际协作体2018-2019学年七年级下学期数学期末试卷
试卷更新日期:2020-06-12 类型:期末考试
一、选择题
-
1. 下面有4个汽车标志图案,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 人体内的淋巴细胞直径约是0.0000051米,将0.0000051用科学记数法表示为( )A、0.51×10﹣5 B、0.51×105 C、5.1×10﹣6 D、0.51×1063. 下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
2. 人体内的淋巴细胞直径约是0.0000051米,将0.0000051用科学记数法表示为( )A、0.51×10﹣5 B、0.51×105 C、5.1×10﹣6 D、0.51×1063. 下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
A、 B、
B、 C、
C、 D、
D、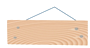 4. 下列事件中,是必然事件的是( )A、打开电视,它正在播广告 B、抛掷一枚硬币,正面朝上 C、打雷后会下雨 D、367人中有至少两人的生日相同5. 下列运算正确的是( )A、a5+a5=a10 B、a6×a4=a24 C、a0÷a﹣1=a D、(a2)3=a56. 若a2﹣b2= ,a﹣b= ,则a+b的值为( )A、﹣ B、 C、﹣3 D、37. 如图,直线l1∥l2 , 以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=70°,则∠1=( )
4. 下列事件中,是必然事件的是( )A、打开电视,它正在播广告 B、抛掷一枚硬币,正面朝上 C、打雷后会下雨 D、367人中有至少两人的生日相同5. 下列运算正确的是( )A、a5+a5=a10 B、a6×a4=a24 C、a0÷a﹣1=a D、(a2)3=a56. 若a2﹣b2= ,a﹣b= ,则a+b的值为( )A、﹣ B、 C、﹣3 D、37. 如图,直线l1∥l2 , 以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=70°,则∠1=( )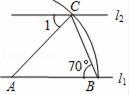 A、40° B、20° C、60° D、70°8. 如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的角平分线交AC于点D,DE⊥AB于E点,下列四个结论中正确的有( )
A、40° B、20° C、60° D、70°8. 如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的角平分线交AC于点D,DE⊥AB于E点,下列四个结论中正确的有( )①DE=DC;②BE=BC;③AD=DC;④△BDE≌△BDC.
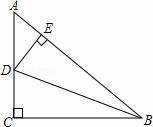 A、1个 B、2个 C、3个 D、4个9. 如图,一只蚂蚁以均匀的速度沿台阶A1⇒A2⇒A3⇒A4⇒A5爬行,那么蚂蚁爬行的高度h随时间t变化的图象大致是( )
A、1个 B、2个 C、3个 D、4个9. 如图,一只蚂蚁以均匀的速度沿台阶A1⇒A2⇒A3⇒A4⇒A5爬行,那么蚂蚁爬行的高度h随时间t变化的图象大致是( )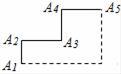 A、
A、 B、
B、 C、
C、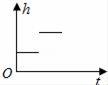 D、
D、 10. 如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角(如:∠1=∠2,∠3=∠4).当小球第1次碰到长方形的边时的点为Q,第2次碰到长方形的边时的点为M…,第2019次碰到长方形的边时的点为图中的( )
10. 如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角(如:∠1=∠2,∠3=∠4).当小球第1次碰到长方形的边时的点为Q,第2次碰到长方形的边时的点为M…,第2019次碰到长方形的边时的点为图中的( )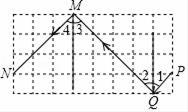 A、N点 B、Q点 C、M点 D、P点
A、N点 B、Q点 C、M点 D、P点二、填空题
-
11. 0.250×4﹣1= .12. 如图所示,转盘被等分成4个扇形,并在上面依次写上数字1,2,3,5,若自由转动转盘,当它停止转动时,指针指向奇数区的概率是 .
 13. 如图,已知∠B=∠DEF,AB=DE,请添加一个条件使△ABC≌△DEF,则需添加的条件是 .
13. 如图,已知∠B=∠DEF,AB=DE,请添加一个条件使△ABC≌△DEF,则需添加的条件是 .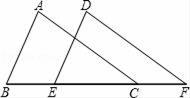 14. 如图所示,直角三角板的60°角压在一组平行线上,AB∥CD,∠ABE=36°,则∠EDC=度.
14. 如图所示,直角三角板的60°角压在一组平行线上,AB∥CD,∠ABE=36°,则∠EDC=度.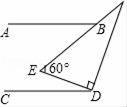 15. 某水果店五一期间开展促销活动,卖出苹果数量x(千克)与售价y(千克/元)的关系如下表:
15. 某水果店五一期间开展促销活动,卖出苹果数量x(千克)与售价y(千克/元)的关系如下表:数量x(千克)
1
2
3
4
5
…
售价y(千克/元)
9
15
21
27
33
…
则售价y(千克/元)与数量x(千克)之间的关系式是 .
16. 如图,两个正方形边长分别为a、b,如果a+b=7,ab=13,则阴影部分的面积为 .
三、解答题
-
17. 计算:(1)、(2x)3•y3+16xy2(2)、(x+2)(2x﹣3)﹣x(x+1)18. 如图,∠ACB=90°,∠A=35°,∠BCD=55°.试说明:AB∥CD.
 19. 先化简,再求值:[(2x﹣y)2+(2x﹣y)(2x+y)+4xy]÷4x,其中x=﹣ ,y=4.20. 如图所示,口袋中有5张完全相同的卡片,分别写有2cm,4cm,6cm,8cm和10cm,袋外有两张卡片,分别写有6cm和10cm,现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,求这三条线段能构成等腰三角形的概率.
19. 先化简,再求值:[(2x﹣y)2+(2x﹣y)(2x+y)+4xy]÷4x,其中x=﹣ ,y=4.20. 如图所示,口袋中有5张完全相同的卡片,分别写有2cm,4cm,6cm,8cm和10cm,袋外有两张卡片,分别写有6cm和10cm,现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,求这三条线段能构成等腰三角形的概率.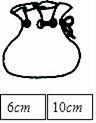 21. 如图,在△ABC中,AB=AC.
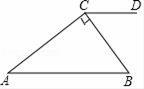
21. 如图,在△ABC中,AB=AC.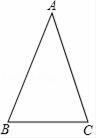 (1)、尺规作图:作∠CBD=∠A,D点在AC边上(要求:不写作法,保留作图痕迹)(2)、若∠A=40°,求∠ABD的度数.22. 周末,小梅骑自行车去外婆家,从家出发0.5小时后到达甲地,在甲地游玩一段时间后,按原速继续前进,小梅出发2小时后,爸爸骑摩托车沿小梅骑自行车的路线追赶小梅,如图是他们离家的路程y(千米)与小梅离家时间x(小时)的关系图,已知爸爸骑摩托车的速度是小梅骑自行车速度的3倍.
(1)、尺规作图:作∠CBD=∠A,D点在AC边上(要求:不写作法,保留作图痕迹)(2)、若∠A=40°,求∠ABD的度数.22. 周末,小梅骑自行车去外婆家,从家出发0.5小时后到达甲地,在甲地游玩一段时间后,按原速继续前进,小梅出发2小时后,爸爸骑摩托车沿小梅骑自行车的路线追赶小梅,如图是他们离家的路程y(千米)与小梅离家时间x(小时)的关系图,已知爸爸骑摩托车的速度是小梅骑自行车速度的3倍.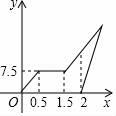 (1)、小梅在甲地游玩时间是小时.
(1)、小梅在甲地游玩时间是小时.小梅骑车的速度是千米/小时.
(2)、若爸爸与小梅同时到达外婆家,求小梅家到外婆家的路程.23. 如图,BE,AD是△ABC的高且相交于点P,点Q是BE延长线上的一点. (1)、试说明:∠1=∠2;(2)、若AP=BC,BQ=AC,线段CP与CQ会相等吗?请说明理由.24. 规定两数a,b之间的一种新运算※,如果ac=b,那么a※b=c.
(1)、试说明:∠1=∠2;(2)、若AP=BC,BQ=AC,线段CP与CQ会相等吗?请说明理由.24. 规定两数a,b之间的一种新运算※,如果ac=b,那么a※b=c.例如:因为52=25,所以5※25=2,因为50=1,所以5※1=0.
(1)、根据上述规定,填空:2※8=2※ = .(2)、在运算时,按以上规定:设4※5=x,4※6=y,请你说明下面这个等式成立:4※5+4※6=4※30.25. 如图,已知长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD=16,BC=DA=24,E为CD边的中点,P为长方形ABCD边上的动点,动点P以4个单位/秒的速度从A出发,沿着A→B→C→E运动到E点停止,设点P运动的时间为t秒,△APE的面积为y. (1)、求当t=2时,y的值是;当t=6时,y的值是 .(2)、当点P在BC上时,求出y与t之间的关系式;(3)、当P在线段BC上运动到某一时刻时,△APE的周长最小时,求此时∠PAB的度数.
(1)、求当t=2时,y的值是;当t=6时,y的值是 .(2)、当点P在BC上时,求出y与t之间的关系式;(3)、当P在线段BC上运动到某一时刻时,△APE的周长最小时,求此时∠PAB的度数.