福建省莆田市城厢区2018-2019学年七年级下学期数学期末试卷
试卷更新日期:2020-06-12 类型:期末考试
一、精心选一选
-
1.
如图,若△DEF是由△ABC经过平移后得到的,则平移的距离是( )
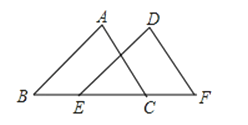 A、线段BC的长度 B、线段BE的长度 C、线段EC的长度 D、线段EF的长度2. 在平面直角坐标系中,点P(1,﹣2)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 为了解游客对“秀屿土海湿地公园、荔城花海山前村、涵江白塘秋月湖和城厢风景九龙谷”这四个风景区旅游的满意程度,数学小组的同学商议了几个收集数据的方案:方案一:在多家旅游公司调查400名导游;方案二:在城厢风景九龙谷调查400名游客;方案三:在秀屿土海湿地公园调查400名游客;方案四:在上述四个景区各调查100名游客,在这四个收集数据的方案中,最合理的是( )A、方案一 B、方案二 C、方案三 D、方案四4. 下列不等式中,不含有x=﹣1这个解的是( )A、2x+1≤﹣3 B、2x﹣1≥﹣3 C、﹣2x+1≥3 D、﹣2x﹣1≤35. 无理数 在数轴上表示时的大概位置是( )
A、线段BC的长度 B、线段BE的长度 C、线段EC的长度 D、线段EF的长度2. 在平面直角坐标系中,点P(1,﹣2)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 为了解游客对“秀屿土海湿地公园、荔城花海山前村、涵江白塘秋月湖和城厢风景九龙谷”这四个风景区旅游的满意程度,数学小组的同学商议了几个收集数据的方案:方案一:在多家旅游公司调查400名导游;方案二:在城厢风景九龙谷调查400名游客;方案三:在秀屿土海湿地公园调查400名游客;方案四:在上述四个景区各调查100名游客,在这四个收集数据的方案中,最合理的是( )A、方案一 B、方案二 C、方案三 D、方案四4. 下列不等式中,不含有x=﹣1这个解的是( )A、2x+1≤﹣3 B、2x﹣1≥﹣3 C、﹣2x+1≥3 D、﹣2x﹣1≤35. 无理数 在数轴上表示时的大概位置是( ) A、E点 B、F点 C、G点 D、H点6. 如图,天平左盘中物体A的质量为 ,天平右盘中每个砝码的质量都是1g,则 的取值范围在数轴上可表示为( )
A、E点 B、F点 C、G点 D、H点6. 如图,天平左盘中物体A的质量为 ,天平右盘中每个砝码的质量都是1g,则 的取值范围在数轴上可表示为( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,直线AB、CD相交于点O,OE⊥AB于O,∠EOC=35°,则∠AOD的度数为( )
7. 如图,直线AB、CD相交于点O,OE⊥AB于O,∠EOC=35°,则∠AOD的度数为( ) A、35° B、55° C、115° D、125°8. 若 是关于x和y的二元一次方程ax+y=1的解,则a的值等于( )A、3 B、1 C、﹣1 D、﹣39. 已知四边形ABCD是平行四边形(即AB∥CD,AD∥BC),则下列各图中∠1与∠2能用来说明命题“内错角相等”的反例的是( )A、
A、35° B、55° C、115° D、125°8. 若 是关于x和y的二元一次方程ax+y=1的解,则a的值等于( )A、3 B、1 C、﹣1 D、﹣39. 已知四边形ABCD是平行四边形(即AB∥CD,AD∥BC),则下列各图中∠1与∠2能用来说明命题“内错角相等”的反例的是( )A、 B、
B、 C、
C、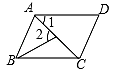 D、
D、 10. 王老师的数学课采用小组合作学习方式,把班上40名学生分成若干小组,如果要求每小组只能是5人或6人,则有几种分组方案( )A、4 B、3 C、2 D、1
10. 王老师的数学课采用小组合作学习方式,把班上40名学生分成若干小组,如果要求每小组只能是5人或6人,则有几种分组方案( )A、4 B、3 C、2 D、1二、精心填一填
-
11. 4是的算术平方根.12. 若点M(a+4,a﹣3)在y轴上,则a= .13. 为了解某校七年级500名学生的身高情况,从中抽取了100名学生进行测量,其中有30名学生的身高在165cm以上,则该问题中的样本容量是 .14. 《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 . 类似地,图2所示的算筹图我们可以表述为 .
 15. 关于x的不等式ax>b的解集是x ,写出一组满足条件的a,b的值:a= .16. 如图,点A、B为定点,直线l∥AB,P是直线l上一动点,对于下列各值:①线段AB的长;②△PAB的周长;③△PAB的面积;④∠APB的度数,其中不会随点P的移动而变化的是(填写所有正确结论的序号) .
15. 关于x的不等式ax>b的解集是x ,写出一组满足条件的a,b的值:a= .16. 如图,点A、B为定点,直线l∥AB,P是直线l上一动点,对于下列各值:①线段AB的长;②△PAB的周长;③△PAB的面积;④∠APB的度数,其中不会随点P的移动而变化的是(填写所有正确结论的序号) .
三、耐心做一做
-
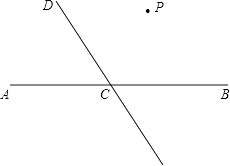
17. 计算:18. 解不等式组: ,并将解集在数轴上表示.19. 读句画图:如图,直线CD与直线AB相交于C,根据下列语句画图:
 (1)、过点P作PQ∥CD,交AB于点Q;(2)、过点P作PR⊥CD,垂足为R.20. 为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器160台,A型号家用净水器进价是1500元/台,售价是2100元/台,B型号家用净水器进价是3500元/台,售价是4300元/台.为保证售完这160台家用净水器的毛利润不低于116000元,求A型号家用净水器最多能购进多少台?(注:毛利润=售价﹣进价)21. 如图,已知∠EGB=90°,AD⊥BG,∠E=∠F.求证:AD是∠BAC平分线.
(1)、过点P作PQ∥CD,交AB于点Q;(2)、过点P作PR⊥CD,垂足为R.20. 为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器160台,A型号家用净水器进价是1500元/台,售价是2100元/台,B型号家用净水器进价是3500元/台,售价是4300元/台.为保证售完这160台家用净水器的毛利润不低于116000元,求A型号家用净水器最多能购进多少台?(注:毛利润=售价﹣进价)21. 如图,已知∠EGB=90°,AD⊥BG,∠E=∠F.求证:AD是∠BAC平分线. 22. 某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:
22. 某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:组别
分数段(x)
频数
A
0≤x<60
2
B
60≤x<70
5
C
70≤x<80
17
D
80≤x<90
a
E
90≤x≤100
b

根据图表中的信息解答下列问题:
(1)、七年级二班学生的人数为 , 频数分布表中a的值为;(2)、已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,佔计该市本次测试成绩达到优秀的人数;(3)、小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.23. 对于平面直角坐标系xOy中的点P(a,b)(其中点P非原点),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P'为点P的“k倍伸长点”.例如:P(1,4)的“2倍伸长点”为P'(1+2×4,2×1+4),即P'(9,6).(1)、若点P的“3倍伸长点”P′的坐标为(6,2),求点P的坐标;(2)、点P的“k倍伸长点”为P′点,若PP′∥y轴且线段PP′的长度不少于线段OP的长度的2倍,求k的取值范围.24. 如图1,已知AD∥BC,∠B=∠D. (1)、求证:AB∥CD;(2)、如图2,点E为BA延长线上一点,∠EAD与∠BCD的角平分线交于点P.
(1)、求证:AB∥CD;(2)、如图2,点E为BA延长线上一点,∠EAD与∠BCD的角平分线交于点P.①求∠APC的度数;
②连接DP,若∠PDC=75°,直接写出 的度数.
25. 如图,在平面直角坐标系中,直线l交x轴于A点、交y轴于点B,下表列举是直线上的点P(x,y)的取值情况:

x
……
﹣4
﹣3
﹣2
﹣1
0
……
y
……
0
1
2
3
4
……
(1)、直线l上的点P(x,y)的横纵坐标之间满足的数量关系是 .A、y=﹣x﹣4, B、y=﹣x+4, C、y=x﹣4, D、y=x+4,(2)、请你根据(1)中的结论,完成以下问题:①若直线l上两点E(e,﹣1)、F(1,f),将线段EF平移到GH(点E的对应点为G,点F的对应点为H),且点G、H都在坐标轴上,求点G的坐标;
②已知坐标平面内第一象限的点M(m,n)、N(m+4,n+4),若三角形PMN的面积是12,求m、n的数量关系.