江西省南昌市2018-2019学年八年级下学期数学期末试卷

试卷更新日期：2020-06-12 类型：期末考试

进入出卷网下载

一、选择题

1. 与﹣ $\sqrt{3}$ 可以合并的二次根式是（　　）

A、 $\sqrt{6}$ B、﹣ $\sqrt{9}$ C、 $\sqrt{12}$ D、﹣ $\sqrt{15}$

查看试题解析
2. 在▱ABCD中，若∠A＝50°，则下列各式中，不能成立的是（　　）

A、∠B＝130° B、∠B+∠C＝180° C、∠C＝50° D、∠B+∠D＝180°

查看试题解析
3. 若五箱苹果的质量（单位：kg）分别为18，21，18，19，20，则这五箱苹果质量的中位数和众数分别是（　　）

A、18和18 B、19和18 C、20和18 D、20和19

查看试题解析
4. 已知数据：1，2，0，2，﹣5，则下列结论错误的是（　　）

A、平均数为0 B、中位数为1 C、众数为2 D、方差为34

查看试题解析
5. 如图，在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段，其中能构成一个直角三角形三边的线段是（　　）

A、CD、EF、GH B、AB、EF、GH C、AB、CD、GH D、AB、CD、EF

查看试题解析
6. 若点P（a，b）是正比例函数y＝ $- \frac{2}{3}$ x图象上任意一点，则下列等式一定成立的是（　　）

A、2a+3b＝0 B、2a﹣3b＝0 C、3a+2b＝0 D、3a﹣2b＝0

查看试题解析
7. 顺次连接四边形四条边的中点，所得的四边形是菱形，则原四边形一定是（　　）

A、平行四边形 B、对角线相等的四边形 C、矩形 D、对角线互相垂直的四边

查看试题解析
8. 如图，已知一条直线经过点A（0，2）、点B（1，0），将这条直线向左平移与x轴、y轴分别交于点C、点D．若DB＝DC，则直线CD的函数解析式为（　　）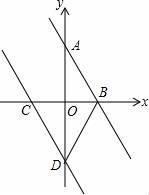

A、y＝﹣2x+2 B、y＝2x﹣2 C、y＝﹣x﹣2 D、y＝﹣2x﹣2

查看试题解析

二、填空题

9. 若 $\sqrt{{(a - 1)}^{2}}$ ＝1﹣a，则a的取值范围为．

查看试题解析
10.
如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm到D，则橡皮筋被拉长了 cm．

查看试题解析
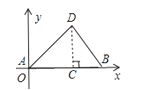11. 若直线y＝kx﹣3经过点（1，﹣2）和点（0，b），则k﹣b的值是．

查看试题解析
12. 如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处．若AB＝3，AD＝4，则ED的长为．

查看试题解析
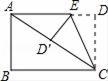13. 若五个整数由小到大排列后，中位数为4，唯一的众数为2，则这组数据之和的最小值是．

查看试题解析
14. 如图，在平行四边形ABCD中，已知AB＝2，BC＝3，∠B＝45°，点P在BC边上，若以A、B、P为顶点的三角形是等腰三角形，则BP的长是．

查看试题解析

三、解答题

15.

(1)、计算：3（ $\sqrt{3}$ -1）﹣| $\sqrt{3}$ ﹣2|；

(2)、简化： $\frac{\sqrt{3 a}}{2 b} \cdot (\sqrt{\frac{b}{a}} \div 2 \sqrt{\frac{3}{b}})$ ．

查看试题解析
16. 如果一组数据3，2，2，4，x的平均数为3．

(1)、求x的值；

(2)、求这组数据的众数．

查看试题解析
17. 如图，在菱形ABCD中，点P是BC的中点，仅用无刻度的直尺按要求画图．（保留作图痕迹，不写作法）

(1)、在图①中画出AD的中点H；

(2)、在图②中的菱形对角线BD上，找两个点E、F，使BE＝DF．

查看试题解析
18. 如图，直线y＝kx+b与x轴相交于点A，与y轴相交于点B，且OA＝1，AB＝ $\sqrt{5}$ ．

(1)、求直线AB的解析式；

(2)、若在直线AB上有一点P，使△POB的面积为4，求点P的坐标．

查看试题解析

四、解答题

19. 如图，四边形ABCD中，对角线AC、BD相交于点O，AO＝CO，BO＝DO，且∠ABC+∠ADC＝180°．

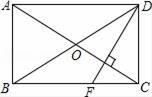(1)、求证：四边形ABCD是矩形．

(2)、DF⊥AC，若∠ADF：∠FDC＝3：2，则∠BDF的度数是多少？

查看试题解析

20. 某校八年级学生开展踢毽子比赛活动，每班选派5名学生参加，在规定时间内每人踢100个

以上（含100个）为优秀，下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个），请根据表中数据解答下列问题：

	1号	2号	3号	4号	5号	总分
甲班	90	100	96	116	98	500
乙班	100	95	108	92	105	500

(1)、计算甲、乙两班的优秀率；

(2)、求出甲、乙两班比赛数据的中位数和方差；

(3)、根据（1）（2）的计算结果，请你判定甲班与乙班的比赛名次．

查看试题解析

21. 为发展旅游经济，我市某景区对门票釆用灵活的售票方法吸引游客．门票定价为50元/人，非节假日打a折售票，节假日按团队人数分段定价售票，即m人以下（含m人）的团队按原价售票；超过m人的团队，其中m人仍按原价售票，超过m人部分的游客打b折售票．设某旅游团人数为x人，非节假日购票款为y₁（元），节假日购票款为y₂（元）．y₁与y₂之间的函数图象如图所示．
、

(1)、观察图象可知：a＝；b＝；m＝；

(2)、写出y₁ ， y₂与x之间的函数关系式；

(3)、某旅行社导游王娜于5月1日带A团，5月20日（非节假日）带B团都到该景区旅游，共付门票款1900元，A，B两个团队合计50人，求A，B两个团队各有多少人？

查看试题解析

五、探究题（本大题共1小题，共10分）

22. 在数学兴趣小组活动中，小明将边长为2的正方形ABCD与边长为2 $\sqrt{2}$ 的正方形AEFG按如图1方式放置，AD与AE在同一条直线上，AB与AG在同一条直线上．

(1)、请你猜想BE与DG之间的数量与位置关系，并加以证明；

(2)、在图2中，若将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，求出BE的长；

(3)、在图3中，若将正方形ABCD绕点A继续逆时针旋转，且线段DG与线段BE相交于点H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．

查看试题解析