福建省福州市平潭县城关教研片2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-12 类型:期末考试
一、选择題
-
1. 若关于x的方程(m﹣2)x2+mx﹣3=0是一元二次方程,则m的取值范围是( )A、m≠2 B、m=2 C、m>2 D、m≠02. 线段a、b、c组成的三角形不是直角三角形的是( )A、a=7,b=24,c=25 B、a= ,b=4,c=5 C、a= ,b=1,c= D、a=40,b=50,c=603. 一组数据2,3,5,5,4的众数、中位数分别是( )A、5,4 B、5,5 C、5,4.5 D、5,3.84. 等腰三角形的周长为20,设底边长为x,腰长为y,则y关于x的函数解析式为( )(x为自变量)A、y=20﹣x B、y=20﹣2x C、y=10﹣ x D、y=20﹣ x5. 把一元二次方程x2﹣6x+1=0配方成(x+m)2=n的形式,正确的是( )A、(x+3)2=10 B、(x﹣3)2=10 C、(x+3)2=8 D、(x﹣3)2=86. 不能判定四边形ABCD为平行四边形的题设是( )A、AB=CD,AB∥CD B、∠A=∠C,∠B=∠D C、AB=AD,BC=CD D、AB=CD,AD=BC7. 对于方程:x(x+1)=0,下列判断正确的是( )A、只有一个实数根 B、有两个不同的实数根 C、有两个相同的实数根 D、没有实数根8. 一次函数y=kx﹣1的图象经过点P且y的值随x的增大而增大,则点P的坐标可以为( )A、(﹣5,3) B、(5,﹣1) C、(2,1) D、(1,﹣3)9. “龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )
 A、赛跑中,兔子共休息了50分钟 B、乌龟在这次比赛中的平均速度是0.1米/分钟 C、兔子比乌龟早到达终点10分钟 D、乌龟追上兔子用了20分钟10. 如图,矩形ABCD中,AB>AD,AN平分∠DAB,DM⊥AN,CN⊥AN,MN为垂足若AB=a,则DM+CN的值为( )
A、赛跑中,兔子共休息了50分钟 B、乌龟在这次比赛中的平均速度是0.1米/分钟 C、兔子比乌龟早到达终点10分钟 D、乌龟追上兔子用了20分钟10. 如图,矩形ABCD中,AB>AD,AN平分∠DAB,DM⊥AN,CN⊥AN,MN为垂足若AB=a,则DM+CN的值为( ) A、a B、 a C、 D、
A、a B、 a C、 D、二、填空题
-
11. 平行四边形ABCD中,∠A=80°,则∠C=°.12. 若数据x1 , x2 , …,xn的方差为6,则数据x1+2,x2+2,…,xn+2的方差是 .13. 直角三角形的两直角边长分别为6和8,则斜边中线的长是 .14. 确定一个b(b≠0)的值为 , 使一元二次方程x2+2bx+1=0无实数根.15. 如图,在正方形ABCD中,点A(a,0),点B(0,b),a>0,b>0,则点C的坐标为 . (用a、b表示)
 16. 若一次函数y=kx+k+2的图象不经过第一象限,则k的取值范围为 .
16. 若一次函数y=kx+k+2的图象不经过第一象限,则k的取值范围为 .三、解答题
-
17. 解方程:2x(x+1)=x+118. 如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.
求证:DE=BF.
 19. 已知一次函数的图象经过点A(3,5)与点B(﹣4,﹣9)(1)、求这个一次函数的解析式;(2)、若点P(a,m)和点Q(a+1,n)在此一次函数的图象上,比较m,n的大小.20. 证明:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
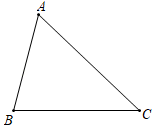
19. 已知一次函数的图象经过点A(3,5)与点B(﹣4,﹣9)(1)、求这个一次函数的解析式;(2)、若点P(a,m)和点Q(a+1,n)在此一次函数的图象上,比较m,n的大小.20. 证明:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.(要求:在给出的△ABC中用尺规作出AB、AC边的中点M、N , 保留作图痕迹,不要求写作法,并根据图形写出已知、求证和证明)
 21. 甲、乙两名队员的10次射击训练,成绩分别被制成下列两个统计图,并整理分析数据如下表:0平均成绩/环中位数/环众数/环方差甲a 7 7 1.2 乙7 b 8 c
21. 甲、乙两名队员的10次射击训练,成绩分别被制成下列两个统计图,并整理分析数据如下表:0平均成绩/环中位数/环众数/环方差甲a 7 7 1.2 乙7 b 8 c (1)、求a,b,c的值;(2)、分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?22. 李师傅去年开了一家商店.今年1月份开始盈利,2月份盈利3000元,4月份的盈利达到4320元,且从2月到4月,每月盈利的平均增长率都相同.(1)、求每月盈利的平均增长率;(2)、按照这个平均增长率,预计5月份这家商店的盈利可达到多少元?23. 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以一定的速度沿同一路线行走,设甲乙两人相距s(米),甲行走的时间为t(分),s为t的函数,其函数图象的一部分如图所示.
(1)、求a,b,c的值;(2)、分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?22. 李师傅去年开了一家商店.今年1月份开始盈利,2月份盈利3000元,4月份的盈利达到4320元,且从2月到4月,每月盈利的平均增长率都相同.(1)、求每月盈利的平均增长率;(2)、按照这个平均增长率,预计5月份这家商店的盈利可达到多少元?23. 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以一定的速度沿同一路线行走,设甲乙两人相距s(米),甲行走的时间为t(分),s为t的函数,其函数图象的一部分如图所示. (1)、求甲、乙两人行走的速度各是多少;(2)、M是该函数图象上的点,求当甲乙两人行走在途中相遇时点M的坐标;(3)、当甲出发多少分钟时,甲、乙两人相距300米?24. 如图,现有一张边长为8的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连结BP、BH.
(1)、求甲、乙两人行走的速度各是多少;(2)、M是该函数图象上的点,求当甲乙两人行走在途中相遇时点M的坐标;(3)、当甲出发多少分钟时,甲、乙两人相距300米?24. 如图,现有一张边长为8的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连结BP、BH. (1)、求证:∠APB=∠BPH;(2)、求证:AP+HC=PH;(3)、当AP=2时,求PH的长.25. 已知y关于x的一次函数y=mx+2﹣2m(m≠0且m≠1),其图象交x轴于点A,交y轴于点B.(0为坐标系的原点)(1)、若OB=6,求这时m的值;(2)、对于m≠0的任意值,该函数图象必过一定点,请求出定点的坐标;(3)、是否存在m的值,使△OAB的面积为8?若存在,求出m的值;若不存在,请说明理由.
(1)、求证:∠APB=∠BPH;(2)、求证:AP+HC=PH;(3)、当AP=2时,求PH的长.25. 已知y关于x的一次函数y=mx+2﹣2m(m≠0且m≠1),其图象交x轴于点A,交y轴于点B.(0为坐标系的原点)(1)、若OB=6,求这时m的值;(2)、对于m≠0的任意值,该函数图象必过一定点,请求出定点的坐标;(3)、是否存在m的值,使△OAB的面积为8?若存在,求出m的值;若不存在,请说明理由.