江西省上饶市婺源县2018-2019学年八年级下学期数学期末试卷

试卷更新日期：2020-06-12 类型：期末考试

进入出卷网下载

一、选择题

1. $\sqrt{\frac{1}{3}}$ 等于（　　）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{3}$ C、3 D、3 $\sqrt{3}$

查看试题解析
2. 下列四组线段中，可以构成直角三角形的是（　　）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、2，3，4 C、1，2，3 D、4，5，6

查看试题解析
3. 一次函数y=-x+1的图象不经过的象限是（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，以正方形ABCD的边AB为一边向外作等边△ABE，则∠BED的度数为（　　）

A、55° B、45° C、40° D、42.5°

查看试题解析
5. 某交警在一个路口统计的某时段来往车辆的车速情况如表：

车速（km/h）

48

49

50

51

52

车辆数（辆）

5

4

8

2

1

则上述车速的中位数和众数分别是（）

A、50，8 B、50，50 C、49，50 D、49，8

查看试题解析
6. 如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是（）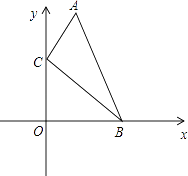

A、（0，0） B、（0，1） C、（0，2） D、（0，3）

查看试题解析

二、填空题

7. 函数y= $\sqrt{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
8. 计算： $\sqrt{2} (\sqrt{2} + 1)$ =

查看试题解析
9. 甲、乙两人进行射击测试，每人10次射击成绩的平均数都是8.5环，方差分别是：
S_甲²=2，S_乙²=1.5，则射击成绩较稳定的是（填“甲”或“乙“）．

查看试题解析
10. 实数a在数轴上的位置如图所示，则|a-1|+ $\sqrt{{(a - 2)}^{2}}$ =.

查看试题解析
11. 边长为5cm的菱形，一条对角线长是6cm，则另一条对角线的长是　　cm．

查看试题解析
12. 在Rt△ABC中，∠C=90°，△ABC的周长为 $\sqrt{6}$ +2，其中斜边的长为2，则这个三角形的面积为

查看试题解析
13. 如图，函数y=2x和y=ax+5的图象相交于A（m，3），则不等式2x＜ax+5的解集为

查看试题解析
14. 如图，在一张长为7cm，宽为5cm的矩形纸片上，现要剪下一个腰长为4cm的等腰三角形，要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上，则剪下的等腰三角形一腰上的高为.

查看试题解析

三、（本大题共5小题，每小题6分，共30分）

15. 计算：

(1)、 $\sqrt{8} + \sqrt{12} - | \sqrt{2} - \sqrt{3} |$

(2)、 $(3 - \sqrt{7}) (3 + \sqrt{7}) + \sqrt{2} (2 - \sqrt{2})$

查看试题解析
16. 如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB，交BC于点D，若CD=1，求AC的长．

查看试题解析
17. 一组数据从小到大顺序排列后为：1，4，6，x，其中位数和平均数相等，求x的值．

查看试题解析
18. 已知y-2和x成正比例，且当x=1时，当y=4．

(1)、求y与x之间的函数关系式；

(2)、若点P（3，m）在这个函数图象上，求m的值．

查看试题解析
19. 已知：如图，在▱ABCD中，对角线AC，BD交于点O，AB⊥AC，AB=1，BC= $\sqrt{5}$ ．

(1)、求平行四边形ABCD的面积S_▱ABCD；

(2)、求对角线BD的长．

查看试题解析

四、（本大题共3小题，每小题8分，共24分）

20. 已知：a、b、c满足 ${(a - \sqrt{8})}^{2} + \sqrt{b - 5} + | c - 3 \sqrt{2} | = 0$ 求：

(1)、a、b、c的值；

(2)、试问以a、b、c为边能否构成三角形？若能构成三角形，求出三角形的周长；若不能构成三角形，请说明理由．

查看试题解析
21. 2014年1月，国家发改委出台指导意见，要求2015年底前，所有城市原则上全面实行居民阶梯水价制度．小明为了解市政府调整水价方案的社会反响，随机访问了自己居住小区的部分居民，就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查，并把调查结果整理绘制成下面的统计图（图1，图2）．

小明发现每月每户的用水量在5m³-35m³之间，有8户居民对用水价格调价涨幅抱无所谓，不会考虑用水方式的改变，根据小明绘制的图表和发现的信息，完成下列问题：

(1)、n= ，小明调查了户居民，并补全图2；

(2)、每月每户用水量的中位数和众数分别落在什么范围？

(3)、如果小明所在小区有1800户居民，请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少？

查看试题解析
22. 如图①，一个正方体铁块放置在圆柱形水槽内，现以一定的速度往水槽中注水，28s时注满水槽．水槽内水面的高度y（cm）与注水时间x（s）之间的函数图象如图②所示．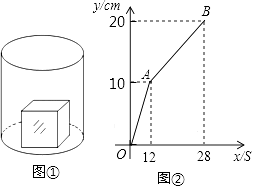

(1)、正方体的棱长为cm；

(2)、求线段AB对应的函数解析式，并写出自变量x的取值范围；

(3)、如果将正方体铁块取出，又经过t（s）恰好将此水槽注满，直接写出t的值．

查看试题解析

五、（本大题共1小题，共10分）

23.
如图，已知∠ABC=90°，D是直线AB上的点，AD=BC．

(1)、如图1，过点A作AF⊥AB，并截取AF=BD，连接DC、DF、CF，判断△CDF的形状并证明

(2)、如图2，E是直线BC上一点，且CE=BD，直线AE、CD相交于点P，∠APD的度数是一个固定的值吗？若是，请求出它的度数；若不是，请说明理由．

查看试题解析

车速（km/h）	48	49	50	51	52
车辆数（辆）	5	4	8	2	1