福建省三明市沙县、建宁县2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-12 类型:期末考试
一、选择题
-
1. 下列各数中,是不等式x>2的解的是A、 B、0 C、1 D、32. 下列图形中是中心对称图形但不是轴对称图形的是A、
 B、
B、 C、
C、 D、
D、 3. 六边形的内角和是( )A、540° B、720° C、900° D、360°4. 已知a<b,则下列不等式一定成立的是A、 B、 C、 D、5. 如图,在 中, , 分别为 , 的中点,若 ,则 的长为
3. 六边形的内角和是( )A、540° B、720° C、900° D、360°4. 已知a<b,则下列不等式一定成立的是A、 B、 C、 D、5. 如图,在 中, , 分别为 , 的中点,若 ,则 的长为 A、3 B、4 C、5 D、66. 若 , ,则代数式 的值为A、1 B、 C、 D、67. 在四边形 中,给出下列条件:① ;② ;③ ;④ ,选其中两个条件不能判断四边形 是平行四边形的是A、①② B、①③ C、①④ D、②④8. 函数 的图象如图所示,则关于 的不等式 的解集是 ( )
A、3 B、4 C、5 D、66. 若 , ,则代数式 的值为A、1 B、 C、 D、67. 在四边形 中,给出下列条件:① ;② ;③ ;④ ,选其中两个条件不能判断四边形 是平行四边形的是A、①② B、①③ C、①④ D、②④8. 函数 的图象如图所示,则关于 的不等式 的解集是 ( ) A、 B、 C、 D、9. 如图,在 中, , , ,将 绕点 逆时针旋转 得到△ ,连接 ,则 的长为
A、 B、 C、 D、9. 如图,在 中, , , ,将 绕点 逆时针旋转 得到△ ,连接 ,则 的长为 A、 B、 C、4 D、610. 如图:已知 ,点 、 在线段 上且 ; 是线段 上的动点,分别以 、 为边在线段 的同侧作等边 和等边 ,连接 ,设 的中点为 ;当点 从点 运动到点 时,则点 移动路径的长是
A、 B、 C、4 D、610. 如图:已知 ,点 、 在线段 上且 ; 是线段 上的动点,分别以 、 为边在线段 的同侧作等边 和等边 ,连接 ,设 的中点为 ;当点 从点 运动到点 时,则点 移动路径的长是 A、5 B、4 C、3 D、0
A、5 B、4 C、3 D、0二、填空题
-
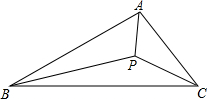
11. 分解因式: .12. “等边对等角”的逆命题是.13. 在 中, ,则 .14. 若分式 的值为0,则x的值为 .15. 已知一次函数 ,当 时,对应的函数 的取值范围是 , 的值为 .16. 如图, 中, , , , 是 内部的任意一点,连接 , , ,则 的最小值为 .
三、解答题
-
17. 分解因式: .18. 如图,在平行四边形ABCD中,E、F分别是BC、AD上的点,且BE=DF.求证:AE=CF.
 19. 解不等式组 并将解集在数轴上表示出来.20. 在平面直角坐标系中, 的三个顶点的位置如图所示,点 的坐标是 ,现将 平移,使点 变换为点 ,点 、 分别是 、 的对应点.
19. 解不等式组 并将解集在数轴上表示出来.20. 在平面直角坐标系中, 的三个顶点的位置如图所示,点 的坐标是 ,现将 平移,使点 变换为点 ,点 、 分别是 、 的对应点. (1)、请画出平移后的△ (不写画法);(2)、并直接写出点 、 的坐标: 、 ;(3)、若 内部一点 的坐标为 ,则点 的对应点 的坐标是 .21. 如图,在 中, ,AB=AC.
(1)、请画出平移后的△ (不写画法);(2)、并直接写出点 、 的坐标: 、 ;(3)、若 内部一点 的坐标为 ,则点 的对应点 的坐标是 .21. 如图,在 中, ,AB=AC. (1)、请用尺规作图的方法在边 上确定点 ,使得点 到边 的距离等于 的长;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求证: .22. 定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如: ,则 是“和谐分式”.(1)、下列分式中,属于“和谐分式”的是(填序号);
(1)、请用尺规作图的方法在边 上确定点 ,使得点 到边 的距离等于 的长;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求证: .22. 定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如: ,则 是“和谐分式”.(1)、下列分式中,属于“和谐分式”的是(填序号);① ;② ;③ ;④
(2)、将“和谐分式” 化成一个整式与一个分子为常数的分式的和的形式为: =;(3)、应用:先化简 ,并求x取什么整数时,该式的值为整数.23. 如图,已知四边形 为平行四边形, 于点 , 于点 . (1)、求证: ;(2)、若 、 分别为边 、 上的点,且 ,证明:四边形 是平行四边形.24. 在2018春季环境整治活动中,某社区计划对面积为 的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为 区域的绿化时,甲队比乙队少用5天.(1)、求甲、乙两工程队每天能完成绿化的面积;(2)、设甲工程队施工 天,乙工程队施工 天,刚好完成绿化任务,求 关于 的函数关系式;(3)、若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.25. 如图1,在 中, , , 是 边上一点,以 为边作 ,使 , .
(1)、求证: ;(2)、若 、 分别为边 、 上的点,且 ,证明:四边形 是平行四边形.24. 在2018春季环境整治活动中,某社区计划对面积为 的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为 区域的绿化时,甲队比乙队少用5天.(1)、求甲、乙两工程队每天能完成绿化的面积;(2)、设甲工程队施工 天,乙工程队施工 天,刚好完成绿化任务,求 关于 的函数关系式;(3)、若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.25. 如图1,在 中, , , 是 边上一点,以 为边作 ,使 , . (1)、直接写出 的度数(用含 的式子表示);(2)、以 , 为边作平行四边形 ,
(1)、直接写出 的度数(用含 的式子表示);(2)、以 , 为边作平行四边形 ,①如图2,若点 恰好落在 上,求证: ;
②如图3,若点 恰好落在 上,求证: .