福建省泉州市泉港区2018-2019学年八年级下学期数学期末试卷
试卷更新日期：2020-06-12 类型：期末考试
一、选择题
-
1. 在平面直角坐标系中，点P（﹣2，﹣3）在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列式子中，可以表示为a﹣3的是（ ）A、a2÷a5 B、a5÷a2 C、a﹣1×a3 D、（a）（﹣a）（﹣a）3. 使分式 有意义的x的取值范围是（ ）A、x≠1 B、x≠﹣1 C、x＜1 D、x＞14. 下列图形既是轴对称图形，又是中心对称图形的是（ ）A、三角形 B、菱形 C、角 D、平行四边形5. 一次函数y=﹣2x+3的图象不经过的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图，在▱ABCD中，若∠A+∠C＝130°，则∠D的大小为（ ）
A、100° B、105° C、110° D、115°7. 如图，矩形ABCD被对角线AC．BD分成四个小三角形，这四个小三角形的周长之和是68，AC＝10．则矩形ABCD的周长是（ ）
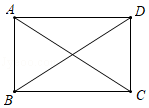A、48 B、38 C、28 D、148. 如图，直线y＝ax（a≠0）与反比例函数y＝ （k≠0）的图象交于A，B两点．若点B的坐标是（3，5），则点A的坐标是（ ）
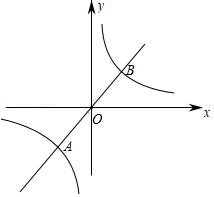A、（﹣3，﹣5） B、（﹣5，﹣3） C、（3．﹣5） D、（5，﹣3）9. 为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗，获得苗高（单位：cm）的平均数与方差为： = =13， = =15：s甲2=s丁2=3.6，s乙2=s丙2=6.3．则麦苗又高又整齐的是（ ）
A、甲 B、乙 C、丙 D、丁10. 如图，▱ABCD中，AE⊥BC于点E，AF⊥CD于点F，AB＝9，AF＝12，AE＝8．则BC等于（ ）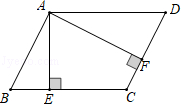
A、20 B、 C、 D、17二、填空题
-
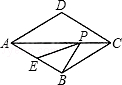
11. 某公司测试自动驾驶5G技术，发现移动中汽车“5G”通信中每个IP数据包传输的测量精度约为0.0000018秒，请将数据0.0000018用科学记数法表示为 ．12. 计算 ＝ ．13. 小明参加岗位应聘中，专业知识、工作经验、仪表形象三项的得分分别为：16分、16分、13分．若这三项的重要性之比为5：3：2，则他最终得分是分．14. 将直线y＝2x﹣3平移，使之经过点（9，3），则平移后的直线是 ．15. 如图，菱形ABCD中，AB＝2，∠BAD＝60°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是 ．
16. 已知△ABC的顶点坐标分別是A（0，1），B（5，1），C（5，﹣6），过A点的直线L：y＝ax+b与BC相交于点E．若AE分△ABC的面积比为1：2，则点E的坐标为 ．三、解答题
-
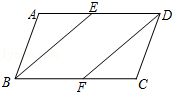
17. 先化简，再求值： ，其中x＝﹣2．18. 如图，在▱ABCD中，E，F分别在AD，BC上，且AE＝CF，连结BE、DF．
求证：BE＝DF．
19. 小李在学校“青少年科技创新比赛”活动中，设计了一个沿直线轨道做匀速直线运动的模型．甲车从A处出发向B处行驶，同时乙车从B处出发向A处行驶．如图所示，线段l1、l2分别表示甲车、乙车离B处的距离y（米）与已用时间x（分）之间的关系．试根据图象，解决以下问题：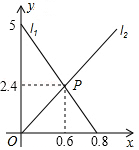
(1)、填空：出发（分）后，甲车与乙车相遇，此时两车距离B处（米）；(2)、求乙车行驶12（分）时与B处的距离．20. 在正方形ABCD中，BE平分∠CBD交边CD于E点．
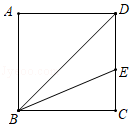(1)、尺规作图：过点E作EF⊥BD于F；（保留作图痕迹，不写作法）；(2)、在（1）的条件下，连接FC，求∠BCF的度数．21. 甲、乙两队共同承担一项“退耕返林”的植树任务，甲队单独完成此项任务比乙队单独完成此项任务多用8天，且甲队单独植树7天和乙队单独植树5天的工作量相同．(1)、甲、乙两队单独完成此项任务各需多少天？(2)、甲、乙两队共同植树5天后，乙队因另有任务停止植树，剩下的由甲队继续植树．为了能够在规定时间内完成任务，甲队增加人数，使工作效率提高到原来的2倍．那么甲队至少再单独施工多少天？22. 如图，▱ABCD的对角线AC、BD相交于点O，对角线AC绕点O逆时针旋转，分别交边DC，AB于点E、F．
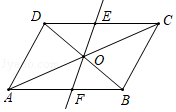(1)、求证：CE＝AF(2)、若DB＝2，BC＝1，CD＝ ．当AC绕点O逆时针方向旋转45°时，判断四边形BEDF的形状，并说明理由．23. 某市开展“环境治理留住青山绿水，绿色发展赢得金山银山”活动，对其周边的环境污染进行综合治理.2018年对A、B两区的空质量进行监测，将当月每天的空气污染指数（简称：API）的平均值作为每个月的空污染指数，并将2018年空气污染指数绘制如下表．据了解，空气污染指数≤50时，空质量为优；50＜空污染指数≤100时，空质量为良；100＜空气污染指数≤150时，质量为轻微污染．月份/地区
1
2
3
4
5
6
7
8
9
10
11
12
A区
115
108
85
100
95
50
80
70
50
50
100
45
B区
105
95
90
80
90
60
90
85
60
70
90
45
(1)、请求出A、B两区的空气污染指数的平均数；(2)、请从平均数、众数、中位数、方差等统计量中选两个对A区、B区的空气质量进行有效对比，说明哪一个地区的环境状况较好．24. （如图，四边形ABCD在平面直角坐标系的第一象限内，其四个顶点分别在反比例函数y1＝ 与y2＝ 的图象上，对角线AC⊥BD于点P，AC⊥x轴于点N（2，0）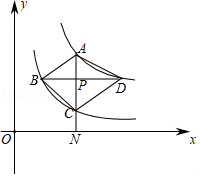
(1)、若CN＝ ，试求n的值；(2)、当n＝2，点P是线段AC的中点时，试判断四边形ABCD的形状，并说明理由；(3)、直线AB与y轴相交于E点．当四边形ABCD为正方形时，请求出OE的长度．25. 如图①，矩形ABCD中，AB＝4，AD＝3，点P是CD边上的一动点（点P与D、C点不重合），四边形ABCP沿AP折叠得四边形AFEP，延长CD交AF于点N．
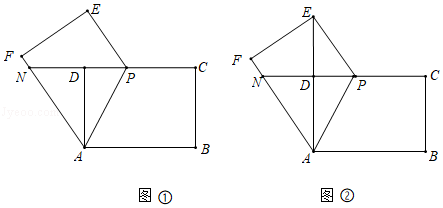(1)、求证：NA＝NP(2)、如图②，若点E恰好在AD的延长线上时，试求出DP的长度；(3)、当∠PAD＝30°时，求证：△DEF是等腰三角形．