福建省泉州市惠安县2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-12 类型:期末考试
一、选择题
-
1. 若分式 在实数范围内有意义,则实数 的取值范围是A、 B、 C、 D、2. 在平面直角坐标系中,点 的位置在A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 目前,随着制造技术的不断发展,手机芯片制造即将进入 (纳米)制程时代.已知 ,则 用科学记数法表示为A、 B、 C、 D、4. 若x=4是分式方程 的根,则a的值为A、9 B、 C、13 D、5. 在平面直角坐标系中,点 与点 关于原点对称,则a+b的值为A、-1 B、-3 C、1 D、36. 小杨同学五次数学小测成绩分别是91分、95分、85分、95分、100分,则小杨这五次成绩的众数和中位数分别是A、95分、95分 B、85分、95分 C、95分、85分 D、95分、91分7. 如图,矩形 中,对角线 、 交于点 .若 ,AC=10,则AB的长为
 A、6 B、5 C、4 D、38. 如图,在 中,AC=a,若 的周长为13,则 的周长为
A、6 B、5 C、4 D、38. 如图,在 中,AC=a,若 的周长为13,则 的周长为 A、 B、 C、 D、9. 如图,点 为正方形 内一点, , ,连结 ,那么 的度数是
A、 B、 C、 D、9. 如图,点 为正方形 内一点, , ,连结 ,那么 的度数是 A、 B、 C、 D、10. 如图,一次函数y=-x+1的图象与两坐标轴分别交于 、 两点,点 是线段AB上一动点(不与点A、B重合),过点C分别作CD、CE垂直于x轴、y轴于点D、E,当点C从点A开始向点B运动时,则矩形CDOE的周长
A、 B、 C、 D、10. 如图,一次函数y=-x+1的图象与两坐标轴分别交于 、 两点,点 是线段AB上一动点(不与点A、B重合),过点C分别作CD、CE垂直于x轴、y轴于点D、E,当点C从点A开始向点B运动时,则矩形CDOE的周长 A、不变 B、逐渐变大 C、逐渐变小 D、先变小后变大
A、不变 B、逐渐变大 C、逐渐变小 D、先变小后变大二、填空题
-
11. 计算: .12. 已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 .13. 若 ,则 .14. 函数 为任意实数)的图象必经过定点,则该点坐标为 .15. 如图, 的顶点 在矩形 的边 上,点 与点 、 不重合,若 的面积为4,则图中阴影部分两个三角形的面积和为 .
 16. 如图,将矩形 绕点 顺时针旋转 度 ,得到矩形 .若 ,则此时 的值是 .
16. 如图,将矩形 绕点 顺时针旋转 度 ,得到矩形 .若 ,则此时 的值是 .
三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 .19. 王老师计划用36元购买若干袋洗衣液,恰遇超市降价促销,每袋洗衣液降价3元,因而王老师只用24元便可以购买到相同袋数的洗衣液.问这种洗衣液每袋原价是多少元?20. 体育课上,甲、乙两个小组进行定点投篮对抗赛,每组10人,每人投10次.下表是甲组成绩统计表:
投进个数
10个
8个
6个
4个
人数
1个
5人
2人
2人
(1)、请计算甲组平均每人投进个数;(2)、经统计,两组平均每人投进个数相同且乙组成的方差为3.2.若从成续稳定性角度看,哪一组表现更好?21. 如图,在 中, 、 是对角线 上两点,且 ,四边形 是平行四边形吗?请说明理由.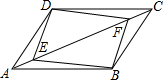 22. 甲车从 地驶往 地,同时乙车从 地驶往 地,两车相向而行,匀速行驶,甲车距 地的距离 与行驶时间 之间的函数关系如图所示,乙车的速度是
22. 甲车从 地驶往 地,同时乙车从 地驶往 地,两车相向而行,匀速行驶,甲车距 地的距离 与行驶时间 之间的函数关系如图所示,乙车的速度是 (1)、求甲车的速度;(2)、当甲乙两车相遇后,乙车速度变为 ,并保持匀速行驶,甲车速度保持不变,结果乙车比甲车晚38分钟到达终点,求 的值.23. 设 是 轴上的一个动点,它与原点的距离为 .(1)、求 关于 的函数解析式,并画出这个函数的图象;(2)、若反比例函数 的图象与函数 的图象相交于点 ,且点 的纵坐标为2.
(1)、求甲车的速度;(2)、当甲乙两车相遇后,乙车速度变为 ,并保持匀速行驶,甲车速度保持不变,结果乙车比甲车晚38分钟到达终点,求 的值.23. 设 是 轴上的一个动点,它与原点的距离为 .(1)、求 关于 的函数解析式,并画出这个函数的图象;(2)、若反比例函数 的图象与函数 的图象相交于点 ,且点 的纵坐标为2.①求 的值;
②结合图象,当 时,写出 的取值范围.