福建省宁德市八年级2018-2019学年八年级下学期数学期末试卷

试卷更新日期：2020-06-12 类型：期末考试

进入出卷网下载

一、选择题

1. 下面的图形中，既是中心对称又是轴对称的图形是（　　）

A、 B、 C、 D、

查看试题解析
2. 如图，将平行四边形ABCD的一边BA延长至点E，若∠EAD＝70°，则∠C等于（　　）

A、110° B、35° C、70° D、55°

查看试题解析
3. 若代数式 $\frac{a + 1}{a - 1}$ 在实数范围内有意义，则实数a的取值范围是（　　）

A、a≥1 B、a≠1 C、a＜1 D、a＝﹣1

查看试题解析
4. 如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，AD＝BD，若AC＝3，BC＝4，则CD的长是（　　）

A、 $\frac{12}{5}$ B、 $\frac{5}{12}$ C、 $\frac{5}{2}$ D、 $\frac{2}{5}$

查看试题解析
5. 如图，△ABC经过平移后得到△DEF，下列说法错误的是（　　）

A、AB∥DE B、∠ACB＝∠DFE C、AD＝BE D、∠ABC＝∠CBE

查看试题解析
6. 如图，DE⊥AC，BF⊥AC，垂足分别是E，F，且DE＝BF，若利用“HL”证明△DEC≌△BFA，则需添加的条件是（　　）

A、EC＝FA B、DC＝BA C、∠D＝∠B D、∠DCE＝∠BAF

查看试题解析
7. 小颖同学准备用26元买笔和笔记本，已知一支笔2元，一本笔记本3元，他买了5本笔记本，最多还能买多少支笔？设他还能买x支笔，则列出的不等式为（　　）

A、2x+3×5≤26 B、2x+3×5≥26 C、3x+2×5≤26 D、3x+2×5≥26

查看试题解析
8. 若从n边形的一个顶点出发，最多可以作3条对角线，则该n边形的内角和是（　　）

A、540° B、720° C、900° D、1080°

查看试题解析
9. 在平面直角坐标系内，点O是原点，点A的坐标是（3，4），点B的坐标是（3，﹣4），要使四边形AOBC是菱形，则满足条件的点C的坐标是（　　）

A、（﹣3，0） B、（3，0） C、（6，0） D、（5，0）

查看试题解析
10. 如图，在正方形ABCD中，分别以点B，C为圆心，BC长为半径画弧，两弧相交于点E，连接AE，BE得到△ABE，则△ABE与正方形ABCD的面积比为（　　）

A、1：2 B、1：3 C、1：4 D、 $1 ： \sqrt{3}$

查看试题解析

二、填空题

11. 化简 $\frac{2 x y}{6 x^{2} y}$ ＝．

查看试题解析
12. 如图，在Rt△ABC中，∠ACB＝90°，CA＝CB，AD是△ABC的角平分线，过点D作DE⊥AB于点E，若CD＝1，则BD＝．

查看试题解析
13. 命题“在△ABC中，如果∠A＝∠B＝∠C，那么△ABC是等边三角形”的逆命题是．

查看试题解析
14. 如图，将△ABC绕点C按逆时针方向旋转得到△DEC，使D点落在AB上，若∠CAB＝66°，则∠BCE的大小是°．

查看试题解析
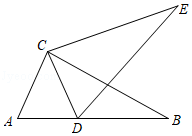15. 如图所示的圆形工件，大圆的半径R为65.4mm，四个小圆的半径r为17.3mm，则图中阴影部分的面积是mm²（结果保留π）．

查看试题解析
16. 已知A，B是一次函数在第一象限图象上的两点，它们的位置如图所示，若点A的横坐标是﹣3m﹣2，点B的横坐标是4，则m的取值范围是．

查看试题解析

三、解答题

17. 因式分解：

(1)、a（a﹣2）+2（a﹣2）；

(2)、3x²﹣6xy+3y² ．

查看试题解析
18. 化简分式： $\frac{x - 3}{x + 3} \div \frac{x^{2} - 6 x + 9}{x^{2} + 3 x} - \frac{2}{3 - x}$

查看试题解析
19. 如图，在△ABC中，AB＝AC，D、E在BC上，且AD＝AE，求证：BD＝CE．

查看试题解析
20. 求不等式组 ${\begin{cases} x + 2 \leq 4 (x - 1) \\ \frac{x}{3} > \frac{x + 2}{5} \end{cases}$ 的解集，并把解集在数轴上表示出来．

查看试题解析
21. 某校为了开展“书香墨香进校园”活动，购买了一批毛笔和墨水．已知毛笔的单位比墨水的单价多5元，购买毛笔用了450元，墨水用了150元，毛笔数量是墨水数量的2倍．求这批毛笔和墨水的数量分别是多少？

查看试题解析
22. 求证：顺次连接对角线相等的四边形的各边中点，所得的四边形是菱形．

(1)、根据所给的图形，将已知、求证补充完整：
已知：如图，在四边形ABCD中，AC＝BD，．

求证：．

(2)、证明这个命题．

查看试题解析
23. 如图，在平面直角坐标系中，△ABC的顶点坐标分别是A（0，1），B（1，3），C（4，3）．

(1)、将△ABC平移得到△A₁B₁C₁ ，且C₁的坐标是（0，﹣1），画出△A₁B₁C₁；

(2)、将△ABC绕点A逆时针旋转90°得到△A₂B₂C₂ ，画出△A₂B₂C₂；

(3)、小娟发现△A₁B₁C₁绕点P旋转也可以得到△A₂B₂C₂ ，请直接写出点P的坐标．

查看试题解析
24. 定义：如果一元一次不等式①的解都是一元一次不等式②的解，那么称一元一次不等式①是一元一次不等式②的蕴含不等式．例如：不等式x＜﹣3的解都是不等式x＜﹣1的解，则x＜﹣3是x＜﹣1的蕴含不等式．

(1)、在不等式x＞1，x＞3，x＜4中，是x＞2的蕴含不等式的是；

(2)、若x＞﹣6是3（x﹣1）＞2x﹣m的蕴含不等式，求m的取值范围；

(3)、若x＜﹣2n+4是x＜2的蕴含不等式，试判新x＜﹣n+3是否是x＜2的蕴含不等式，并说明理由．

查看试题解析
25. 如图1，在△ABC中，∠BAC＝90°，AB＝AC＝5，点D在AC边上，CD＝2，过点D作DE⊥BC于点E，分别以AB，AD为邻边作平行四边形ABFD，连接AE，EF．

(1)、求∠EDF的大小；

(2)、求证：AE＝EF；

(3)、如图2，将图1中的△CDE绕点C旋转，其余条件保持不变，连接AF．求在旋转过程中，线段AF长的最大值．

查看试题解析