福建省龙岩市新罗区2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-12 类型:期末考试
一、选择题
-
1. 下列二次根式中,最简二次根式是A、 B、 C、 D、2. 下列计算正确的是A、 B、 C、 D、3. 已知样本 , , , 的平均数是 2 ,则 , , , 的平均数为A、2 B、2.75 C、3 D、54. 我校男子足球队22名队员的年龄如下表所示:这些队员年龄的众数和中位数分别是( )
年龄 岁
14
15
16
17
18
19
人数
2
1
3
6
7
3
A、18,17 B、17,18 C、18,17.5 D、17.5,185. 若 ,则 的取值范围为A、 B、 C、 D、6. 在 中,若y是x的正比例函数,则k值为A、1 B、 C、 D、无法确定7. 若等腰 的周长是 ,一腰长为xcm,底边长为ycm,则y与x的函数关系式及自变量x的取值范围是A、 B、 C、 D、8. 如图,在 的正方形网格中, 的顶点都在格点上,下列结论错误的是 A、 B、 C、 D、9. 若顺次连结四边形四条边的中点,所得的四边形是菱形,则原四边形一定是( )
A、 B、 C、 D、9. 若顺次连结四边形四条边的中点,所得的四边形是菱形,则原四边形一定是( )
A、平行四边形 B、矩形 C、对角线相等的四边形 D、对角线互相垂直的四边形10. 如图,四边形 中, , ,且 ,以 , , 为边向外作正方形,其面积分别为 , , .若 , ,则 的值为( ) A、8 B、12 C、24 D、60
A、8 B、12 C、24 D、60二、填空题
-
11. 将直线y=2x+1向下平移2个单位,所得直线的表达式是 .
12. 八年级两个班一次数学考试的成绩如下:八(1)班46人,平均成绩为86分;八(2)班54人,平均成绩为80分,则这两个班的平均成绩为分.13. 如图,已知一次函数 与的图象相交于 ,则关于 的不等式 的解集是 .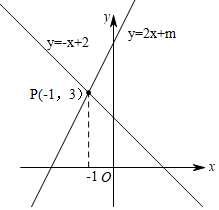 14. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , ,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是 .
14. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , ,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是 .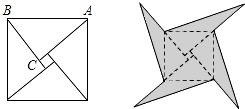 15. 如图,在 中, , , 边上的中线 ,则 的面积是 .
15. 如图,在 中, , , 边上的中线 ,则 的面积是 .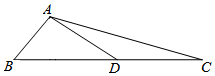 16. 如图,在矩形 中, , ,点 是 边上一点,连接 ,将 沿 折叠,使点 落在点 处.当 为直角三角形时, .
16. 如图,在矩形 中, , ,点 是 边上一点,连接 ,将 沿 折叠,使点 落在点 处.当 为直角三角形时, .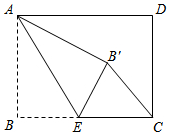
三、解答题
-
17.(1)、计算: ;(2)、已知 ,求代数式 的值.18. 如图,矩形ABCD中,对角线AC的垂直平分线MN与AD相交于点M,与BC相交于点N,连接AN,CM.求证:四边形AMCN是菱形.
 19. 甲、乙两名同学进入八年级后,某科6次考试成绩如图所示:
19. 甲、乙两名同学进入八年级后,某科6次考试成绩如图所示: (1)、请根据统计图填写下表:
(1)、请根据统计图填写下表:平均数
方差
中位数
众数
甲
75
75
乙
33.3
72.5
(2)、请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析,你认为反映出什么问题?①从平均数和方差相结合分析;
②从折线图上两名同学分数的走势上分析.
20. 如图,四边形ABCD是平行四边形,E是AD边上一点. (1)、只用无刻度直尺在 边上作点 ,使得 ,保留作图痕迹,不写作法;(2)、在(1)的条件下,若 , ,求四边形 的周长.21. 求证:矩形的对角线相等.(要求:画出图形,写出已知,求证和证明过程)22. 某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).(1)、分别写出两种优惠方法购买费用 (元 与所买水性笔支数 (支 之间的函数关系式;(2)、对 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;(3)、小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.23. 对于自变量 的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.对于分段函数,在自变量 不同的取值范围内,对应的函数表达式也不同.例如: 是分段函数,当 时,函数的表达式为 ;当 时,函数表达式为 .(1)、请在平面直角坐标系中画出函数 的图象;(2)、当 时,求 的值;(3)、当 时,求自变量 的取值范围.
(1)、只用无刻度直尺在 边上作点 ,使得 ,保留作图痕迹,不写作法;(2)、在(1)的条件下,若 , ,求四边形 的周长.21. 求证:矩形的对角线相等.(要求:画出图形,写出已知,求证和证明过程)22. 某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).(1)、分别写出两种优惠方法购买费用 (元 与所买水性笔支数 (支 之间的函数关系式;(2)、对 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;(3)、小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.23. 对于自变量 的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.对于分段函数,在自变量 不同的取值范围内,对应的函数表达式也不同.例如: 是分段函数,当 时,函数的表达式为 ;当 时,函数表达式为 .(1)、请在平面直角坐标系中画出函数 的图象;(2)、当 时,求 的值;(3)、当 时,求自变量 的取值范围.
