浙江省嘉兴市南湖区2020年数学中考一模试卷
试卷更新日期:2020-06-10 类型:中考模拟
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不给分)
-
1. 下列各组数中,互为相反数的是( )A、4与-4 B、 与4 C、4与 D、-4与2. 下列图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、赵爽弦图
 B、笛卡尔心形线
B、笛卡尔心形线  C、科克曲线
C、科克曲线  D、斐波那契螺旋线
D、斐波那契螺旋线  3. 下列运算正确的是( )A、a+a=a² B、x².x3=x5 C、(a+1)²=a2+1 D、(2x)3=6x34. 有10位同学参加歌唱比赛,成绩各不相同,按成绩取前5位进入决赛,一位选手知道了自己的成绩后,要判断能否进入决赛,则他还需知道这10位同学成绩的( )A、平均数 B、中位数 C、方差 D、众数5. 已知正方形的面积为50,则该正方形的边长介于( )A、6与7之间 B、7与8之间 C、8与9之间 D、9与10之间6. 车队运送一批货物.若每车装4吨,剩下8吨未装;若每车装5吨,则剩余1辆车。甲、乙两人设该车队有x辆车,丙、丁两人设这批货物有y吨,分别列出如下方程:
3. 下列运算正确的是( )A、a+a=a² B、x².x3=x5 C、(a+1)²=a2+1 D、(2x)3=6x34. 有10位同学参加歌唱比赛,成绩各不相同,按成绩取前5位进入决赛,一位选手知道了自己的成绩后,要判断能否进入决赛,则他还需知道这10位同学成绩的( )A、平均数 B、中位数 C、方差 D、众数5. 已知正方形的面积为50,则该正方形的边长介于( )A、6与7之间 B、7与8之间 C、8与9之间 D、9与10之间6. 车队运送一批货物.若每车装4吨,剩下8吨未装;若每车装5吨,则剩余1辆车。甲、乙两人设该车队有x辆车,丙、丁两人设这批货物有y吨,分别列出如下方程:甲:4x+8=5(x-1);乙:4x-8=5(x+1);丙: +1;丁: -1。
其中所列方程正确的是( )
A、甲、丙 B、甲、丁 C、乙、丙 D、乙、丁7. 图1是一张圆形纸片,直径AB=4,现将点A折叠至圆心O形成折痕CD,再把点C,D都折叠至圆心O处,最后将图形打开铺平(如图2所示),则弧EF的长为( ) A、 π B、 π C、 π D、 π8. 已知抛物线y=ax2+bx+c(u>0)交x轴于点A(x1 , 0),B(x2 , 0),且x1<x2 , 点P(m,n)(n<0)在该抛物线上.下列四个判断:①b²-4ac≥0;②若a+c=b+3,则该抛物线一定经过点(1,3);③方程a2+bx+c=n的解是x=m;④当m=
A、 π B、 π C、 π D、 π8. 已知抛物线y=ax2+bx+c(u>0)交x轴于点A(x1 , 0),B(x2 , 0),且x1<x2 , 点P(m,n)(n<0)在该抛物线上.下列四个判断:①b²-4ac≥0;②若a+c=b+3,则该抛物线一定经过点(1,3);③方程a2+bx+c=n的解是x=m;④当m=时,△PAB的面积最大。其中判断一定正确的序号是( )
A、① B、② C、③ D、④9. 如图所示的一个大长方形,它被分割成4个大小不同的正方形①,②,③,④和一个小长方形⑤,若已知大长方形的周长,则一定能计算出周长的图形是( )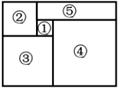 A、②③ B、④⑤ C、②④ D、③⑤10. 如图,平面直角坐标系中,O为原点,点A,B分别在y轴、x轴的正半轴上,△AOB的两条外角平分线交于点P,且点P在反比例函数y= 的图象上。PA,PB的延长线分别交x轴、y轴于点C,D,连结CD,则△OCD的面积是( )
A、②③ B、④⑤ C、②④ D、③⑤10. 如图,平面直角坐标系中,O为原点,点A,B分别在y轴、x轴的正半轴上,△AOB的两条外角平分线交于点P,且点P在反比例函数y= 的图象上。PA,PB的延长线分别交x轴、y轴于点C,D,连结CD,则△OCD的面积是( )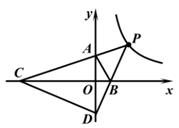 A、8 B、8 C、16 D、16
A、8 B、8 C、16 D、16二、填空题(本题有6小题,每小题4分,共24分)
-
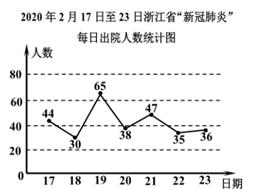
11. 8的立方根是 .12. 已知y是x的函数,且当x>0时,y随x的增大而减小.则这个函数的表达式可以是。(写出一个符合题意的答案即可)13. 方程组: 的解是。14. 如图是2020年2月17一23日浙江省“新冠肺炎”每日出院人数折线统计图,相邻两日间日出院人数增长有快慢,其中最大的增长率是。(精确到0.1%)
 15. 对于实数a,b,c,定义mid{a,b,c}=b(a≥b≥c)。例如mid{-1,1,3}=1;mid{1,2,2}=2,若1≤mid{1,a-1,a+1}≤2,则a的取值范围是。16. 如图,在△ABC中,∠ACB=90°,AB=10,BC=6,P是边AC上的动点,将线段BP绕点B按逆时针方向旋转到BP',旋转角等于∠ABC,连结CP'。
15. 对于实数a,b,c,定义mid{a,b,c}=b(a≥b≥c)。例如mid{-1,1,3}=1;mid{1,2,2}=2,若1≤mid{1,a-1,a+1}≤2,则a的取值范围是。16. 如图,在△ABC中,∠ACB=90°,AB=10,BC=6,P是边AC上的动点,将线段BP绕点B按逆时针方向旋转到BP',旋转角等于∠ABC,连结CP'。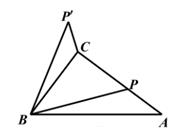 (1)、当P',C,P在一条直线上时,线段AP的长是 。(2)、线段CP'的最小值是。
(1)、当P',C,P在一条直线上时,线段AP的长是 。(2)、线段CP'的最小值是。三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17.(1)、计算:(2)、化简:18. 如图,在平面直角坐标系中,△ABC的各顶点坐标为A(1,1),B(-1,0),C(0,-1)。
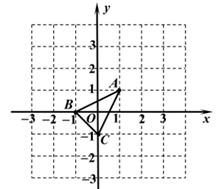 (1)、以坐标原点O为位似中心,在图中作出△ABC的一个位似图形△A'B'C',使它与△ABC的位似比为2。(2)、在(1)的条件下,求 的值。19. 一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y。(1)、用列表法或画树状图法,列出点M(x,y)的所有可能结果。(2)、求点M(x,y)在反比例函数y= 的图象上的概率。20. 如图,在菱形ABCD中,∠A=60°,经过点C且半径为2的⊙O分别切AB,AD于点B,D。
(1)、以坐标原点O为位似中心,在图中作出△ABC的一个位似图形△A'B'C',使它与△ABC的位似比为2。(2)、在(1)的条件下,求 的值。19. 一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y。(1)、用列表法或画树状图法,列出点M(x,y)的所有可能结果。(2)、求点M(x,y)在反比例函数y= 的图象上的概率。20. 如图,在菱形ABCD中,∠A=60°,经过点C且半径为2的⊙O分别切AB,AD于点B,D。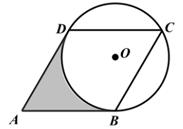 (1)、求 的度数。(2)、求图中阴影部分的面积。
(1)、求 的度数。(2)、求图中阴影部分的面积。 21. 温度的计量,世界上大部分国家都使用摄氏温度(℃),但美、英等国的天气预报仍然使用华氏温度(°F).已知两种计量之间的关系是我们已学的某种函数,且两种计量的部分对应值如下表。
21. 温度的计量,世界上大部分国家都使用摄氏温度(℃),但美、英等国的天气预报仍然使用华氏温度(°F).已知两种计量之间的关系是我们已学的某种函数,且两种计量的部分对应值如下表。摄氏C(℃)
0
10
20
30
40
50
华氏F(°F)
32
50
68
86
104
122
(1)、判断华氏F(°F)与摄氏C(℃)之间是何种函数关系?并求出F(°F)关于C(℃)的函数表达式。(2)、求华氏为0°F时的摄氏温度。(3)、华氏温度的值与对应的摄氏温度的值能否相等?若能,求相等的值;若不能,请说明理由。22. 如图1是一款“雷达式”懒人椅。当懒人椅完全展开时,其侧面示意图如图2所示,金属杆AB,CD在点O处连接,且分别与金属杆EF在点B,D处连接,金属杆CD的OD部分可以伸缩(即OD的长度可变).已知0A=50cm,OB=20cm,OC=30cm,DE=BF=5cm.当把懒人椅完全叠合时,金属杆AB,CD,EF重合在一条直线上(如图3所示),此时点E和点A重合。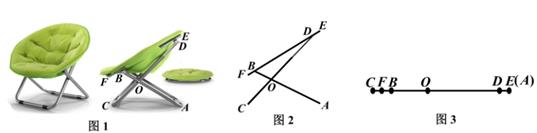 (1)、如图2,已知∠BOD=6∠ODB,∠OBF=140°。
(1)、如图2,已知∠BOD=6∠ODB,∠OBF=140°。①求∠AOC的度数。
②求点A,C之间的距离。
(2)、如图3,当懒人椅完全叠合时,求CF与CD的长。23. 在平面直角坐标系中,P,Q是抛物线y=ax²(a>0)上不重合的两点,点M(0,2),直线PM,QM的比例系数互为相反数。(1)、若点P的坐标为(2,8),求α的值。(2)、在(1)的条件下,求点Q的坐标。(3)、若点P,Q都在第一象限内,且点P的横坐标是点Q的横坐标的3倍,试探究点P与点Q的纵坐标的差是否为定值?若是,求出该定值;若不是,请说明理由。24. 【方法提炼】解答几何问题常常需要添辅助线,其中平移图形是重要的添辅助线策略.
【问题情境】
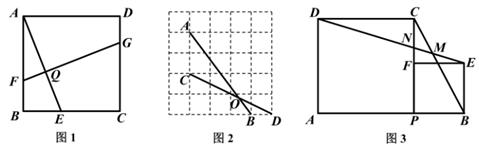
如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q。求证:AE=FG。
小明在分析解题思路时想到了两种平移法:
方法1:平移线段FG使点F与点B重合,构造全等三角形。
方法2:平移线段BC使点B与点F重合,构造全等三角形。
(1)、【尝试应用】请按照小明的思路,选择其中一种方法进行证明.
(2)、如图2,正方形网格中,点A,B,C,D为格点,AB交CD于点O,求tan∠AOC的值。(3)、如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连结DE分别交线段BC,PC于点M,N。①求∠DMC的度数。
②连结AC交DE于点H,求 的值。