广西北部湾(来宾市)2020年初中学业水平考试数学模拟卷(一)
试卷更新日期:2020-06-10 类型:中考模拟
一、选择题(本大题共12小题,每小题3分,共36分)
-
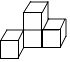
1. -5的绝对值是( )A、-5 B、 C、 D、52. 如图是一个由4个相同正方体组成的立体图形,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 为全力应对疫情,响应政府“停课不停学”号召:某市教育局发布了关于疫情防控期间开展在线课程教学的通知:从2月10日开始.全市中小学按照教学计划,开展在线课程教学和答疑.据互联网后台数据显示,某中学九年级七科老师在2月10日在线答疑的问题总个数如下表所示:
3. 为全力应对疫情,响应政府“停课不停学”号召:某市教育局发布了关于疫情防控期间开展在线课程教学的通知:从2月10日开始.全市中小学按照教学计划,开展在线课程教学和答疑.据互联网后台数据显示,某中学九年级七科老师在2月10日在线答疑的问题总个数如下表所示:学科
语文
数学
英语
物理
化学
道德与法治
历史
数量/个
26
28
28
26
24
21
22
则2月10日该中学九年级七科老师在线答疑问题总个数的平均数是( )
A、22 B、24 C、25 D、264. 下列汽车标志的图形中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列计算中,正确的是( )A、a2·a3=a6 B、a3÷a-3=1 C、(a-b)2=a2-ab+b2 D、(-a2)3=-a66. 如图,已知直线a∥b,将一块含30°角的直角三角板(∠C=90°)按如图所示的位置摆放。若∠1=25,则∠2的度数为( )
5. 下列计算中,正确的是( )A、a2·a3=a6 B、a3÷a-3=1 C、(a-b)2=a2-ab+b2 D、(-a2)3=-a66. 如图,已知直线a∥b,将一块含30°角的直角三角板(∠C=90°)按如图所示的位置摆放。若∠1=25,则∠2的度数为( )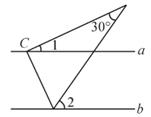 A、55° B、70° C、85° D、65°7. 一个不透明的布袋里装有3个红球、2个黑球、若干个白球.从布袋中随机摸出一个球,摸出的球是红球的是概率是 ,袋中白球共有( )A、3个 B、4个 C、5个 D、6个8. 将抛物线y=2x2向左平移2个单位,再向下平移5个单位得到的抛物线是( )A、y=2(x-2)2-5 B、y=2(x+2)2-3 C、y=2(x+2)2+3 D、y=2(x+2)2-59. 如图,PA,PB是⊙O的切线,A,B为切点,点C,D在⊙O上。若∠P=102°,则∠A+∠C=( )
A、55° B、70° C、85° D、65°7. 一个不透明的布袋里装有3个红球、2个黑球、若干个白球.从布袋中随机摸出一个球,摸出的球是红球的是概率是 ,袋中白球共有( )A、3个 B、4个 C、5个 D、6个8. 将抛物线y=2x2向左平移2个单位,再向下平移5个单位得到的抛物线是( )A、y=2(x-2)2-5 B、y=2(x+2)2-3 C、y=2(x+2)2+3 D、y=2(x+2)2-59. 如图,PA,PB是⊙O的切线,A,B为切点,点C,D在⊙O上。若∠P=102°,则∠A+∠C=( )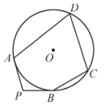 A、220° B、219° C、218” D、217°10. 某消毒液生产厂家自2020年初开始一段时间,日销售量与产量持平,库存始终为m(m≥0)吨.新冠肺炎疫情爆发后,消毒液需求量猛增,在生产能力不变的情况下,消毒液一度脱销,以下函数图象中,能表示2020年初至脱销期间,时间t与库存最y之间函数关系的是( )A、
A、220° B、219° C、218” D、217°10. 某消毒液生产厂家自2020年初开始一段时间,日销售量与产量持平,库存始终为m(m≥0)吨.新冠肺炎疫情爆发后,消毒液需求量猛增,在生产能力不变的情况下,消毒液一度脱销,以下函数图象中,能表示2020年初至脱销期间,时间t与库存最y之间函数关系的是( )A、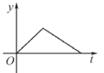 B、
B、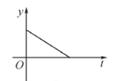 C、
C、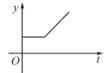 D、
D、 11. 二次函数y=ax2+bx+c(a子0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③若点A(-3,0)、B( ,y2)、C( ,y3)在该函数图象上则y1<y3<y2;④若方程a(x+1)(x-5)=-3的两根为x1和x2 , 且x1<x2 , 则x1≤-1<5<x2 , 其中正确的结论有( )
11. 二次函数y=ax2+bx+c(a子0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③若点A(-3,0)、B( ,y2)、C( ,y3)在该函数图象上则y1<y3<y2;④若方程a(x+1)(x-5)=-3的两根为x1和x2 , 且x1<x2 , 则x1≤-1<5<x2 , 其中正确的结论有( )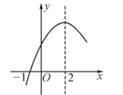 A、1个 B、2个 C、3个 D、4个12. 如图,菱形ABCD的边长为8,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A’MN,连接A’C,则A‘C最小值是( )
A、1个 B、2个 C、3个 D、4个12. 如图,菱形ABCD的边长为8,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A’MN,连接A’C,则A‘C最小值是( )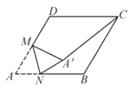 A、4 B、2 +1 C、4 -4 D、8 -4
A、4 B、2 +1 C、4 -4 D、8 -4二、填空题(本大题共6小题,每小题3分,共18分)
-
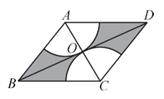
13. 使 无意义的x的取值范围是。14. 分解因式:x2y-4y3=。15. 国家发改委2月7日紧急下达第二批中央预算内投资2亿元人民币,专项补助承担重症感染患者救治任务的湖北多家医院重症治疗病区建设.其中数据2亿元用科学记数法表示为元。16. 如图, 在菱形ABCD中,对角线AC,BD交于点O,∠ABC=60°,AB=2,分别以点A,C为圆心,以AO的长为半径画孤分别与菱形ABCD的边相交,则图中阴影部分的面积为 (结果保留π)
 17. 如图,P为双曲线y= 上的一点,过P作x轴、y轴的垂线,分别交直线y=-2x+m于C,B两点,若直线y=-2x+m与y轴交于点A,与x轴相交于点D,则AC·BD的值为。
17. 如图,P为双曲线y= 上的一点,过P作x轴、y轴的垂线,分别交直线y=-2x+m于C,B两点,若直线y=-2x+m与y轴交于点A,与x轴相交于点D,则AC·BD的值为。 18. 如图, 在平面直角坐标系中,A1(2,1),B1(1,3),C1(1,1),对△A1B1C1按顶点顺次循环作旋转变换如△A1B1C1绕A1顺时针旋转90°得到△A2B2C2;△A2B2C2绕B2顺时针旋转90°得到△A3B3C3;△A3B3C3绕C3顺时针旋转90%,得到△A4B4C4……以此类推,点C103的坐标是。
18. 如图, 在平面直角坐标系中,A1(2,1),B1(1,3),C1(1,1),对△A1B1C1按顶点顺次循环作旋转变换如△A1B1C1绕A1顺时针旋转90°得到△A2B2C2;△A2B2C2绕B2顺时针旋转90°得到△A3B3C3;△A3B3C3绕C3顺时针旋转90%,得到△A4B4C4……以此类推,点C103的坐标是。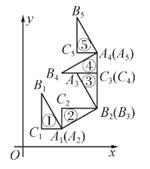
三、解答题(本大题共8题,共66分)
-
19. 计算:(π-3.14)0- +(-1)-1+cos45°20. 解方程: =121. 某校在参加了教育质量综合评价学业素养测试后,随机抽取八年级部分学生,针对发展水平四个维度“阅读素养、数学素养、科学素养、人文素养”,开展了“你最需要提升的学业素养”问卷调查(每名学生必选且只能选择一项).小明、小颖和小雯在协助老师进行统计后,有这样一段对话:
小明:“选‘科学素养‘和’人文素养‘的同学分别为15人,12人。”
小颖:“选‘数学素养'的同学比选阅读素养的同学少4人。”
小雯:“选‘科学素养‘的同学占样本总数的20%。”
(1)、这次抽样调查了多少名学生?(2)、样本总数中,选“阅读素养”“数学素养”的学生各有多少人?(3)、如图是把调查结果整理后绘制成的扇形统计图,请求出相关数据,并在横线上补全。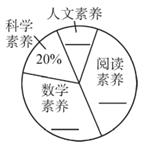 (4)、该校八年级有学生400人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?22. △ABC在平面直角坐标系中的位置如图所示.
(4)、该校八年级有学生400人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?22. △ABC在平面直角坐标系中的位置如图所示.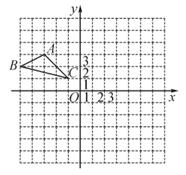 (1)、①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2,且△A1B1C位于点C的异侧,并表示出A1的坐标,
(1)、①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2,且△A1B1C位于点C的异侧,并表示出A1的坐标,②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C。
(2)、在(1)的条件下求出点B经过的路径长。23. 如图,已知△ABC为等腰直角三角形,△ABD为等边三角形,连接CD。
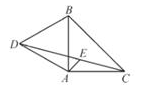 (1)、求∠ACD的度数;(2)、如图,作∠BAC的平分线交CD于点E,求证:DE=AE+CE。
(1)、求∠ACD的度数;(2)、如图,作∠BAC的平分线交CD于点E,求证:DE=AE+CE。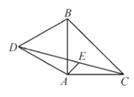 24. 某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价a(元/支)之间满足一次函数关系,且当x=30时,y-100;当x=35时,y=50。(1)、请求出y与x的函数解析式。(2)、该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?(3)、近期武汉爆发了新型冠状病毒疫情,该网店店主决定从每天获得的利润中抽出200元捐赠给武汉,为了保证捐款后每天剩余利润不低于550元,该商品的售价x的取值范用是多少?请说明理由。25. 如图,△ABC内接于⊙O,∠C=45°,BC与直径AD交于点E。
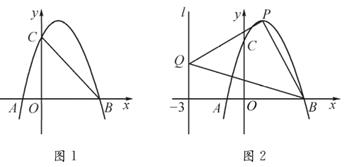
24. 某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价a(元/支)之间满足一次函数关系,且当x=30时,y-100;当x=35时,y=50。(1)、请求出y与x的函数解析式。(2)、该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?(3)、近期武汉爆发了新型冠状病毒疫情,该网店店主决定从每天获得的利润中抽出200元捐赠给武汉,为了保证捐款后每天剩余利润不低于550元,该商品的售价x的取值范用是多少?请说明理由。25. 如图,△ABC内接于⊙O,∠C=45°,BC与直径AD交于点E。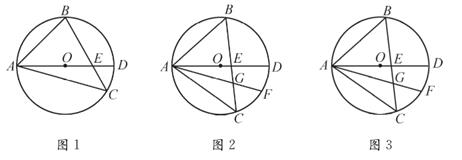 (1)、如图1,若∠BAC=60°,求证:BE=2OE;(2)、如图2,在BC上取点G,使BG=BA,连接AG并延长交⊙O于点F,求证:AF平分∠CAD;(3)、如图3,在(2)的条件下,若AD=10, ,求线段EG的长。26. 如图,抛物线L:y=ar2+bx+c与x轴交于A,B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知抛物线的对称轴为直线x=1。(1)、求抛物线L的解析式。(2)、将抛物线L向下平移h个单位长度, 使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围。(3)、设P是抛物线L上任一点, 点Q在直线l:x=-3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标:若不能,请说明理由。
(1)、如图1,若∠BAC=60°,求证:BE=2OE;(2)、如图2,在BC上取点G,使BG=BA,连接AG并延长交⊙O于点F,求证:AF平分∠CAD;(3)、如图3,在(2)的条件下,若AD=10, ,求线段EG的长。26. 如图,抛物线L:y=ar2+bx+c与x轴交于A,B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知抛物线的对称轴为直线x=1。(1)、求抛物线L的解析式。(2)、将抛物线L向下平移h个单位长度, 使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围。(3)、设P是抛物线L上任一点, 点Q在直线l:x=-3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标:若不能,请说明理由。