江苏省苏州市2020年阳光指标学业水平调研卷数学试卷
试卷更新日期：2020-06-10 类型：中考模拟
一、选择题(本大题共10小题，每小题3分，共30分。)
-
1. 下列方程中，关于x的一元二次方程是（ ）A、x+2=3 B、x+y=1 C、x2-2x-3=0 D、x2+ =12. 某班有6个学习小组，每个小组的人数分别为5、6、5、4、7、5，这组数据的中位数是（ ）A、5 B、6 C、5.5 D、4.53. 如图，在△ABC中，点D，E分别为边AB，AC的中点，若DE=2，则BC的长度为（ ）
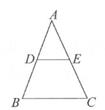A、2 B、3 C、4 D、54. 如图，一个圆形飞镖板被分为四个圆心角相等的扇形，若大圆半径为2，小圆半径为1，则阴影部分的面积为（ ）
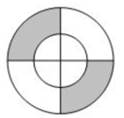A、π B、 π C、3π D、 π5. 二次函数y=x2-2x图像的顶点坐标是（ ）A、(1，1) B、(-1，1) C、(1，-1) D、(-1，-1)6. 关于x的一元二次方程式ax2-2ax-b=0有一个实数根x=1，则下面关于该方程的判别式△的说法正确的是（ ）A、△>0 B、△=0 C、△<0 D、无法确定7. 如图，将矩形ABCD沿对角线AC折叠，点B的对应点为点B'，AB'与CD相交于点F，若AB=3，sin∠CAB= ，则DF的长度是（ ）
A、1 B、2 C、 D、38. 在如图所示的正方形网格中，⊙O的内接△ABC的顶点均为格点，则tanA的值为（ ）
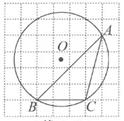A、 B、 C、 D、9. 如图，已知⊙O的弦AB=8，以AB为一边作正方形ABCD，CD边与⊙O相切，切点为E，则⊙O半径为（ ）
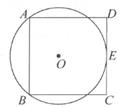A、10 B、8 C、6 D、510. 如图，已知二次函数y=mx2-4mx+3m(m>0)的图像与x轴交于A，B两点，与y轴交于点C，连接AC、BC，若CA平分∠OCB，则m的值为（ ）
A、 B、 C、 D、二、填空题(本大题共8小题，每小题3分，共24分。)
-
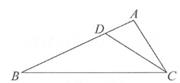
11. 一组数据：1，0，-1，x，2，若它们的平均数是1，则x=。12. 抛掷一枚质地均匀的正方体骰子1次(骰子的六个面分别标有数字1，2，3，4，5，6)，朝上的点数为6的概率为 。13. 若关于x的一元二次方程x2-2x+m=0有实数解，则m的取值范围是。14. 如图，在△ABC中，∠ACD=∠B，AD=1，BD=3，则AC= 。
15. 如图，圆锥的母线长l为5cm，侧面积为10πcm2 ， 则圆锥的底面圆半径r为cm。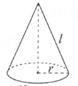
16. 用一根长为20cm的铁丝围成一个矩形，那么这个矩形的面积可能是cm2(写出1个可能的值即可)17. 如图，已知点C处有一个高空探测气球，从点C处测得水平地面上A、B两点的俯角分别为30°和45°，若AB=2km，则A、C两点之间的距离为km。
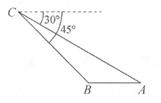18. 如图，在△ABC中，AB=AC=5，BC=6，则△ABC的内切圆⊙I与外接圆⊙O的周长之比为。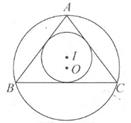
三、解答题(本大题共10小题，共76分。)
-
19. 解方程：x2=2x-120. 计算：2cos30°+|tan60°-1|-21. 如图，若二次函数y=x2-x-2的图像与x轴交于A、B两点(点A在点B的左侧)，与y轴交于C点。
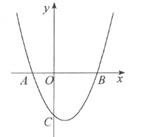(1)、求A、B两点的坐标；(2)、若P(m，-2)为二次函数y=x2-x-2图像上一点，求m的值。22. 在一个不透明的口袋中装有4张卡片，分别印有数字1、2、3、6，这4张卡片除印有的数字不同外，其余都相同。(1)、搅匀后从中任意摸出1张卡片，摸到印有奇数卡片的概率为；(2)、搅匀后从中任意摸出1张卡片，将该卡片印有的数字记为a，再从剩余3张卡片中任意摸出1张卡片，将该卡片印有的数字记为b，请用列表或画树状图的方法求出点P(a，b)在反比例函数y= 图像上的概率。23. 一个两位数的个位数字与十位数字的和为9，并且个位数字与十位数字的平方和为45，求这个两位数。24. 某校开展了“文明城市”活动周，活动周设置了“A：文明礼仪，B：生态环境，C：交通安全，D：卫生保洁”四个主题活动，每个学生限选一个主题参与。为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如下图所示的不完整的条形统计图和扇形统计图。
(1)、本次随机调查的学生人数是人；(2)、补全条形统计图；(3)、在扇形统计图中，“B”主题对应扇形的圆心角为度。25. 如图，从灯塔C处观测轮船A、B的位置，测得轮船A在灯塔C北偏西45°的方向，轮船B在灯塔C北偏东α的方向，且AC=2 海里，BC= 海里，已知tanα=3，求A、B两艘轮船之间的距离。(结果保留根号)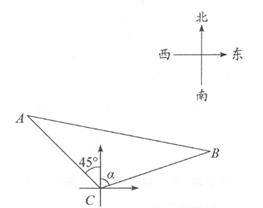
26. 如图，在平面直角坐标系中，二次函数y=ax2+bx+3(a≠0)的图像经过点A(-1，0)，点B(3，0)，与y轴交于点C。
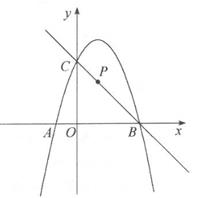(1)、求a、b的值；(2)、若点P为直线BC上一点，点P到A、B两点的距离相等，将该抛物线向左(或向右)平移，得到一条新抛物线，并且新抛物线经过点P，求新抛物线的顶点坐标。27. 如图，四边形ABCD为⊙O的内接四边形，且AC为⊙O的直径， ，延长BC到E，使得BE=AB，连接DE。
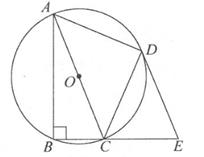(1)、求证：AD=DE；(2)、若DE为⊙O的切线，且DE=2 ，求 的长度。28. 如图①，在矩形ABCD中，已知BC=8cm，点G为BC边上一点，满足BG=AB=6cm，动点E以1cm／s的速度沿线段BG从点B移动到点G，连接AE，作EF⊥AE，交线段CD于点F。设点E移动的时间为t(s)，CF的长度为y(cm)，y与t的函数关系如图②所示
(1)、图①中，CG= cm，图②中，m=；(2)、点F能否为线段CD的中点？若可能，求出此时t的值，若不可能，请说明理由；(3)、在图①中，连接AF、AG，设AG与EF交于点H，若AG平分△AEF的面积，求此时t的值。