江苏省无锡市锡北片2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-06-10 类型:期中考试
一、单选题
-
1. 下列四个图案中,不是中心对称图案的是( )A、
 B、
B、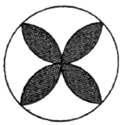 C、
C、 D、
D、 2. 以下问题,适合用抽样调查的是( )A、旅客上飞机前的安检 B、调查市场上酸奶的质量情况 C、疫情期间对进入校园的师生的测温检查 D、某区招聘新教师,对应聘人员的面试3. 小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:
2. 以下问题,适合用抽样调查的是( )A、旅客上飞机前的安检 B、调查市场上酸奶的质量情况 C、疫情期间对进入校园的师生的测温检查 D、某区招聘新教师,对应聘人员的面试3. 小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:通话时间
x/min
0<x≤5
5<x≤10
10<x≤15
15<x≤20
频数
(通话次数)
20
16
9
5
则通话时间不超过15 min的频率为( )
A、0.1 B、0.4 C、0.5 D、0.94. 分式 可变形为( )
A、 B、 C、 D、5. 要使分式 有意义,则x的取值范围是( )A、x>2 B、x<2 C、x≠0 D、x≠26. 菱形的对角线不具备的性质是( )A、对角线互相平分 B、对角线一定相等 C、对角线一定垂直 D、对角线平分一组对角7.如图,▱ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
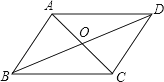 A、10 B、14 C、20 D、228. 如图,已知点E,F分别是四边形ABCD的边AD,BC的中点,G,H分别是对角线BD,AC的中点,要使四边形EGFH是菱形,则四边形ABCD需满足的条件是( )
A、10 B、14 C、20 D、228. 如图,已知点E,F分别是四边形ABCD的边AD,BC的中点,G,H分别是对角线BD,AC的中点,要使四边形EGFH是菱形,则四边形ABCD需满足的条件是( )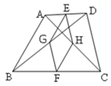 A、AB=CD B、AC=BD C、AC⊥BD D、AD=BC9. 如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A、AB=CD B、AC=BD C、AC⊥BD D、AD=BC9. 如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )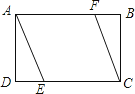 A、 B、 C、1 D、10. 如图,在等边△ABC内有一点D,AD=4,BD=3,CD=5,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则四边形ADCE的面积为( )
A、 B、 C、1 D、10. 如图,在等边△ABC内有一点D,AD=4,BD=3,CD=5,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则四边形ADCE的面积为( )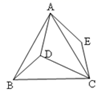 A、12 B、 C、 D、
A、12 B、 C、 D、二、填空题
-
11. 一只不透明的袋子中装有3个黑球、2个白球和1个红球共6个球,现充分搅匀后随机摸出一球,则摸到白球的概率为.12. 如果分式 的值为0,那么x的值是.13. 已知菱形ABCD的对角线AC=12 cm,BD=16cm,则这个菱形的面积为cm.14. 已知 ,则 的值.15. 如图,▱ABCD中,AE平分∠BAD,若∠B=52°,则∠AEC的度数为.
 16. 若用去分母法解分式方程 会产生增根,则m的值为.17. 已知:如图,在△ABC中,点A1 , B1 , C1分别是BC、AC、AB的中点,A2 , B2 , C2分别是B1C1 , A1C1 , A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为.
16. 若用去分母法解分式方程 会产生增根,则m的值为.17. 已知:如图,在△ABC中,点A1 , B1 , C1分别是BC、AC、AB的中点,A2 , B2 , C2分别是B1C1 , A1C1 , A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为.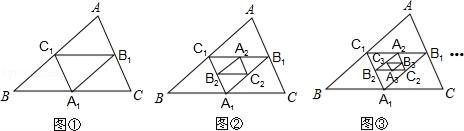 18. 如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边上一点,且 ,以D为一个顶点作正方形DEFG,且DE=BC,连接AE,将正方形DEFG绕点D旋转一周,在整个旋转过程中,当AE取得最大值时AG的长为.
18. 如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边上一点,且 ,以D为一个顶点作正方形DEFG,且DE=BC,连接AE,将正方形DEFG绕点D旋转一周,在整个旋转过程中,当AE取得最大值时AG的长为.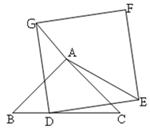
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 解方程:(1)、 = ;(2)、 .21. 先化简,再求值: ,其中a2+a﹣1=0.22. 二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分为非常赞同、赞同、无所谓、不赞同等四种态度.现将调查统计结果制成了如图所示的两幅统计图,请结合这两幅统计图,回答下列问题:
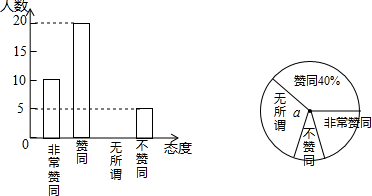 (1)、在这次问卷调查中,一共抽取了名学生,a=%;(2)、请补全条形统计图;(3)、持“不赞同”态度的学生人数的百分比所占扇形的圆心角为°;(4)、若该校有1200名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.23. 按要求作图,不要求写做法,但要保留作图痕迹.(1)、如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.
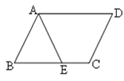
(1)、在这次问卷调查中,一共抽取了名学生,a=%;(2)、请补全条形统计图;(3)、持“不赞同”态度的学生人数的百分比所占扇形的圆心角为°;(4)、若该校有1200名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.23. 按要求作图,不要求写做法,但要保留作图痕迹.(1)、如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.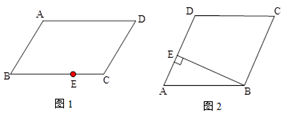 (2)、如图2,BE是菱形ABCD的边AD上的高,请只用直尺(不带刻度)作出菱形ABCD的边AB上的高DF.24. 如图,四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:四边形AECF是平行四边形.
(2)、如图2,BE是菱形ABCD的边AD上的高,请只用直尺(不带刻度)作出菱形ABCD的边AB上的高DF.24. 如图,四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:四边形AECF是平行四边形. 25. 列方程解应用题:马小虎的家距离学校1400米,一天马小虎从家去上学,出发8分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他.已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.26. 在△ABC中,AB=12,AC=BC=10,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为D,点C的对应点为E,连接BD,BE.
25. 列方程解应用题:马小虎的家距离学校1400米,一天马小虎从家去上学,出发8分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他.已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.26. 在△ABC中,AB=12,AC=BC=10,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为D,点C的对应点为E,连接BD,BE. (1)、如图,当α=60°时,延长BE交AD于点F.
(1)、如图,当α=60°时,延长BE交AD于点F.①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长.
(2)、在旋转过程中,过点D作DG垂直于直线AB,垂足为G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.27. 如图,在正方形ABCD中,AB=5cm,E为对角线BD上一动点,连接AE、CE,过E点作EF⊥AE,交直线BC于点F,E点从B点出发,沿BD方向以每秒1cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2 , E点的运动时间为x秒.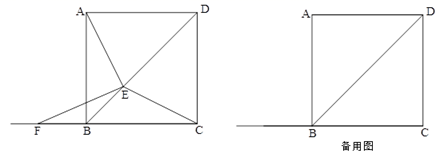 (1)、点E在整个运动过程中,试说明总有:CE=EF;(2)、求y与x之间关系的表达式,并写出x的取值范围.
(1)、点E在整个运动过程中,试说明总有:CE=EF;(2)、求y与x之间关系的表达式,并写出x的取值范围.