河北省唐山市路北区2020年中考数学一模试卷
试卷更新日期:2020-06-10 类型:中考模拟
一、单选题
-
1. sin45°的值等于( )
A、 B、 C、 D、2. 将630万用科学记数法表示为a×10n , 则n的值为( )A、5 B、6 C、7 D、83. 下列手机手势解锁图案中,是轴对称图形的是( )A、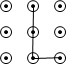 B、
B、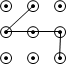 C、
C、 D、
D、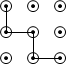 4. 在下列考察中,是抽样调查的是( )A、了解全校学生人数 B、调查某厂生产的鱼罐头质量 C、调查杭州市出租车数量 D、了解全班同学的家庭经济状况5. 计算 的结果是( )A、 B、 C、 D、16. 如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )
4. 在下列考察中,是抽样调查的是( )A、了解全校学生人数 B、调查某厂生产的鱼罐头质量 C、调查杭州市出租车数量 D、了解全班同学的家庭经济状况5. 计算 的结果是( )A、 B、 C、 D、16. 如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )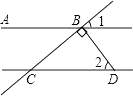 A、40° B、50° C、60° D、140°7. 如图,数轴上所表示关于x的不等式组的解集是( )
A、40° B、50° C、60° D、140°7. 如图,数轴上所表示关于x的不等式组的解集是( ) A、 B、 C、 D、8. 若 的每条边长都增加各自的 ,得到 ,若 的面积为4,则 的面积是( )A、9 B、8 C、6 D、29. 已知关于 的一元二次方程 ,当 时,该方程解的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、不能确定10. 如图,一艘货船在 处,巡逻艇 在其南偏西 的方向上,此时一艘客船在 处,巡逻艇 在其南偏西 的方向上,则此时从巡逻艇上看这两艘船的视角 的度数是( )
A、 B、 C、 D、8. 若 的每条边长都增加各自的 ,得到 ,若 的面积为4,则 的面积是( )A、9 B、8 C、6 D、29. 已知关于 的一元二次方程 ,当 时,该方程解的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、不能确定10. 如图,一艘货船在 处,巡逻艇 在其南偏西 的方向上,此时一艘客船在 处,巡逻艇 在其南偏西 的方向上,则此时从巡逻艇上看这两艘船的视角 的度数是( )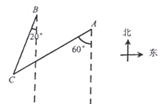 A、 B、 C、 D、 .11. 解分式方程 ,分以下四步,其中错误的一步是( )A、方程两边各分式的最简公分母是 B、方程两边都乘以 ,得整式方程: C、解这个整式方程,得 D、原方程的解为12. 如图,点 都是 上的点, ,则 ( )
A、 B、 C、 D、 .11. 解分式方程 ,分以下四步,其中错误的一步是( )A、方程两边各分式的最简公分母是 B、方程两边都乘以 ,得整式方程: C、解这个整式方程,得 D、原方程的解为12. 如图,点 都是 上的点, ,则 ( )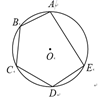 A、 B、 C、 D、13. 某工程队承接了60万平方米的绿化工程,由于情况有变,…设原计划每天绿化的面积为 万平方米,列方程为 ,根据方程可知省路的部分是( )A、实际每天的工作效率比原计划提高了 ,结果提前30天完成了这一任务 B、实际每天的工作效率比原计划提高了 ,结果延误30天完成了这一任务 C、实际每天的工作效率比原计划降低了 ,结果延误30天完成了这一任务 D、实际每天的工作效率比原计划降低了 ,结果提前30天完成了这一任务14. 如图,矩形 中, , ,以 为圆心, 为半径画弧,交 于点 ,以 为圆心, 为半径画弧,交 于点 ,则 的长为( )
A、 B、 C、 D、13. 某工程队承接了60万平方米的绿化工程,由于情况有变,…设原计划每天绿化的面积为 万平方米,列方程为 ,根据方程可知省路的部分是( )A、实际每天的工作效率比原计划提高了 ,结果提前30天完成了这一任务 B、实际每天的工作效率比原计划提高了 ,结果延误30天完成了这一任务 C、实际每天的工作效率比原计划降低了 ,结果延误30天完成了这一任务 D、实际每天的工作效率比原计划降低了 ,结果提前30天完成了这一任务14. 如图,矩形 中, , ,以 为圆心, 为半径画弧,交 于点 ,以 为圆心, 为半径画弧,交 于点 ,则 的长为( )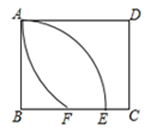 A、3 B、4 C、 D、515. 如图,将函数 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
A、3 B、4 C、 D、515. 如图,将函数 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( ) A、 B、 C、 D、16. 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:
A、 B、 C、 D、16. 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0,②2a+b=O,③b2﹣4ac<0,④4a+2b+c>0其中正确的是( )
 A、①③ B、只有② C、②④ D、③④
A、①③ B、只有② C、②④ D、③④二、填空题
-
17. 因式分解: .18. 已知正方形 和正六边形 边长均为1,如图所示,把正方形放置在正六边形外,使 边与 边重合,按下列步骤操作:将正方形在正六边形外绕点 逆时针旋转,使 边与 边重合,完成第一次旋转;再绕点 逆时针旋转,使 边与 边重合,完成第二次旋转;此时点 经过路径的长为 . 若按此方式旋转,共完成六次,在这个过程中点 , 之间距离的最大值是 .
 19. A、B、C、D四个车站的位置如图所示.
19. A、B、C、D四个车站的位置如图所示. (1)、A、D两站的距离为;(2)、C、D两站的距离为;(3)、若 ,C为AD的中点,b= .
(1)、A、D两站的距离为;(2)、C、D两站的距离为;(3)、若 ,C为AD的中点,b= .三、解答题
-
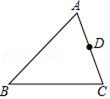
20. 如图,在△ABC中,AB>AC,点D在边AC上.
 (1)、作∠ADE,使∠ADE=∠ACB,DE交AB于点E;(尺规作图,保留作图痕迹,不写作法)(2)、若BC=5,点D是AC的中点,求DE的长.21. 某校开展征文活动,征文主题只能从“爱国”、“敬业”、“诚信”、“友善”四个主题中选择一个,每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
(1)、作∠ADE,使∠ADE=∠ACB,DE交AB于点E;(尺规作图,保留作图痕迹,不写作法)(2)、若BC=5,点D是AC的中点,求DE的长.21. 某校开展征文活动,征文主题只能从“爱国”、“敬业”、“诚信”、“友善”四个主题中选择一个,每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.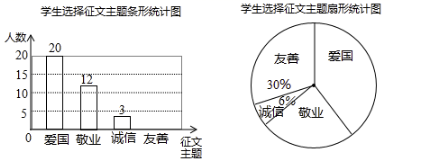 (1)、将上面的条形统计图补充完整;(2)、在扇形统计图中,选择“爱国”主题所对应的圆心角是度;(3)、如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有名;(4)、学生会宣传部有七年级的2名男生和2名女生,现从中随机挑选2名同学参加“主题征文”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.22. 观察下表:
(1)、将上面的条形统计图补充完整;(2)、在扇形统计图中,选择“爱国”主题所对应的圆心角是度;(3)、如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有名;(4)、学生会宣传部有七年级的2名男生和2名女生,现从中随机挑选2名同学参加“主题征文”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.22. 观察下表:序号
1
2
3
…
图形
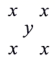


…
我们把某格中字母和所得到的多项式称为特征多项式,例如:
第1格的“特征多项式”为 ;
第2格的“特征多项式”为 .
回答下列问题:
(1)、第3格的“特征多项式”为 ,第4格的“特征多项式”为 ,
第 格的“特征多项式”为;
(2)、若第1格的“特征多项式”的值为 ,第2格的“特征多项式”的值为 ,求 的值;(3)、在(2)的条件下,第 格的特征多项式的值为 ,则直接写出 的值;若没有,请说明理由.23. 如图,在 中, ,点 从点 出发沿 向点 运动,点 从点 出发沿 向点 运动,点 和点 同时出发,速度相同,到达 点或 点后运动停止. (1)、求证: ;(2)、若 ,求 的度数;(3)、若 的外心在其内部时,直接写出 的取值范围.24. 如图,在平面直角坐标系中,直线l1:y=﹣ x与反比例函数y= 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)、求证: ;(2)、若 ,求 的度数;(3)、若 的外心在其内部时,直接写出 的取值范围.24. 如图,在平面直角坐标系中,直线l1:y=﹣ x与反比例函数y= 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2; (1)、求反比例函数的表达式;(2)、根据图象写出﹣ x> 的解集;(3)、将直线l1:y=﹣ x沿y向上平移后的直线l2与反比例函数y= 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.25. 如图1,已知抛物线 与 轴相交于点 ,与 轴相交于点 和点 ,点 在点 的右侧,点 的坐标为 ,将线段 沿 轴的正方向平移 个单位后得到线段 .
(1)、求反比例函数的表达式;(2)、根据图象写出﹣ x> 的解集;(3)、将直线l1:y=﹣ x沿y向上平移后的直线l2与反比例函数y= 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.25. 如图1,已知抛物线 与 轴相交于点 ,与 轴相交于点 和点 ,点 在点 的右侧,点 的坐标为 ,将线段 沿 轴的正方向平移 个单位后得到线段 .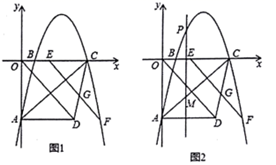 (1)、当 时,点 或点 正好移动到抛物线上;(2)、当点 正好移动到抛物线上, 与 相交于点 时,求 点坐标;(3)、如图2,若点 是 轴上方抛物线上一动点,过点 作平行于 轴的直线交 于点 ,探索是否存在点 ,使线段 长度有最大值?若存在,直接写出点 的坐标和 长度的最大值;若不存在,请说明理由.26. 如图1,点 和矩形 的边 都在直线 上,以点 为圆心,以24为半径作半圆,分别交直线 于 两点.已知: , ,矩形自右向左在直线 上平移,当点 到达点 时,矩形停止运动.在平移过程中,设矩形对角线 与半圆 的交点为 (点 为半圆上远离点 的交点).
(1)、当 时,点 或点 正好移动到抛物线上;(2)、当点 正好移动到抛物线上, 与 相交于点 时,求 点坐标;(3)、如图2,若点 是 轴上方抛物线上一动点,过点 作平行于 轴的直线交 于点 ,探索是否存在点 ,使线段 长度有最大值?若存在,直接写出点 的坐标和 长度的最大值;若不存在,请说明理由.26. 如图1,点 和矩形 的边 都在直线 上,以点 为圆心,以24为半径作半圆,分别交直线 于 两点.已知: , ,矩形自右向左在直线 上平移,当点 到达点 时,矩形停止运动.在平移过程中,设矩形对角线 与半圆 的交点为 (点 为半圆上远离点 的交点).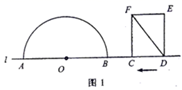 (1)、如图2,若 与半圆 相切,求 的值;
(1)、如图2,若 与半圆 相切,求 的值;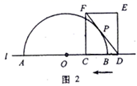 (2)、如图3,当 与半圆 有两个交点时,求线段 的取值范围;
(2)、如图3,当 与半圆 有两个交点时,求线段 的取值范围;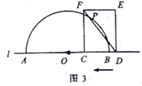 (3)、若线段 的长为20,直接写出此时 的值.
(3)、若线段 的长为20,直接写出此时 的值.