河北省唐山市丰南区2020年中考数学一模试卷

试卷更新日期：2020-06-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 在实数 $0$ ，-2， $| - \sqrt{5} |$ ， $2$ 中，最大的是（）

A、 $0$ B、 $- 2$ C、 $| - \sqrt{5} |$ D、 $2$

查看试题解析
2. 下列计算正确的是（）

A、2x+3y=5xy B、(m+3)²=m²+9 C、(xy²)³=xy⁶ D、a¹⁰÷a⁵=a⁵

查看试题解析
3. 已知：如图，是一几何体的三视图，则该几何体的名称为（　　）

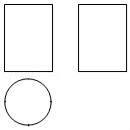A、长方体 B、正三棱柱 C、圆锥 D、圆柱

查看试题解析
4. 如图，数轴上的点A所表示的数为 $x$ ，则 $x^{2}$ -10的立方根为（）

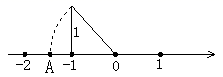A、-8 B、2 C、8 D、-2

查看试题解析
5. 在抛物线y=x²-4上的一个点是（）

A、（4，4） B、（1，－4） C、（2，0） D、（0，4）

查看试题解析
6. 化简 $\frac{a^{2} + a b}{a - b} \div \frac{a b}{a - b}$ 的结果是（）

A、a² B、 $\frac{a^{2}}{a - b}$ C、 $\frac{a - b}{b}$ D、 $\frac{a + b}{b}$

查看试题解析
7. 已知∠AOB，作图.
步骤1：在OB上任取一点M，以点M为圆心，MO长为半径画半圆，分别交OA、OB于点P、Q；

步骤2：过点M作PQ的垂线交 $\overset{⌢}{P Q}$ 于点C；

步骤3：画射线OC.

则下列判断：① $\overset{⌢}{P C}$ = $\overset{⌢}{C Q}$ ；②MC∥OA；③OP=PQ；④OC平分∠AOB，其中正确的个数为（）

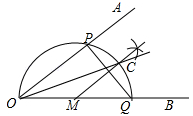A、1 B、2 C、3 D、4

查看试题解析
8. 一个有进水管和出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内即进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（L）与时间x（min）之间的关系如图所示，则每分钟的出水量为（　　）

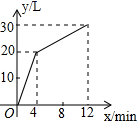A、5L B、3.75L C、2.5L D、1.25L

查看试题解析
9. 如果a、b互为相反数，x、y互为倒数，则 $\frac{1}{4}$ （a+b）+ $\frac{7}{2}$ xy的值是（）

A、2 B、3 C、3.5 D、4

查看试题解析
10.
若函数y=kx＋b的图象如图所示，那么当y>0时，x的取值范围是（）

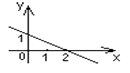A、x>1 B、x>2 C、x<1 D、x<2

查看试题解析
11.
菱形OABC在平面直角坐标系中的位置如图所示．∠AOC=45°，OC= $\sqrt{2}$ ，则点B的坐标为( )

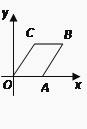A、( $\sqrt{2}$ ， 1) B、(1， $\sqrt{2}$ ) C、( $\sqrt{2}$ +1，1) D、(1， $\sqrt{2}$ +1)

查看试题解析
12. 下列事件中必然发生的事件是（）

A、一个图形旋转后所得的图形与原来的图形不全等 B、100件产品中有4件次品，从中任意抽取5件，至少一件是正品 C、不等式的两边同时乘以一个数，结果仍是不等式 D、随意翻一本书的某页，这页的页码一定是偶数

查看试题解析
13. 《九章算术》记载：今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？译文：今有人合伙购物，每人出8钱，会多3钱；每人出7钱，又会差4钱，问人数、物价各是多少？设合伙人数为 $x$ 人，物价为 $y$ 钱，以下列出的方程组正确的是（　　）

A、 ${\begin{array}{l} y - 8 x = 3 \\ y - 7 x = 4 \end{array}$ B、 ${\begin{array}{l} y - 8 x = 3 \\ 7 x - y = 4 \end{array}$ C、 ${\begin{array}{l} 8 x - y = 3 \\ y - 7 x = 4 \end{array}$ D、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = 4 \end{array}$

查看试题解析
14. 如图所示，AB∥CD，则∠A+∠E+∠F+∠C等于（）

A、180° B、360° C、540° D、720°

查看试题解析
15. 如图，在平面直角坐标系xOy中，A（0，2），B（0，6），动点C在直线y=x上．若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是（）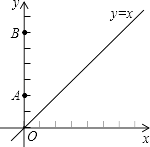

A、2 B、3 C、4 D、5

查看试题解析
16. 下图为歌神KTV的两种计费方案说明.若晓莉和朋友们打算在此KTV的一间包厢里连续欢唱6小时，经服务生计算后，告知他们选择包厢计费方案会比人数计费方案便宜，则他们在同一间包厢里欢唱的至少（　　）

A、6人 B、7人 C、8人 D、9人

查看试题解析

二、填空题

17. 关于x的方程的 $x^{2} - 6 x + m = 0$ 有两个相等的实数根，则m的值为．

查看试题解析
18. 如图，过点O的直线AB与反比例函数y= $\frac{k}{x}$ 的图象交于A，B两点，A（2，1），直线BC∥y轴，与反比例函数y= $\frac{- 3 k}{x}$ （x＜0）的图象交于点C，连接AC，则△ABC的面积为．

查看试题解析
19. 如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足S△PAB＝ $\frac{1}{3}$ S矩形ABCD，则点P到A、B两点距离之和PA+PB的最小值为.

查看试题解析

三、解答题

20.

(1)、如图，已知△ABC中，AB=2，BC=4．画出△ABC的高AD和CE并求出 $\frac{A D}{C E}$ 的值．

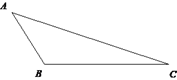(2)、在平面直角坐标系中，O为坐标原点，点A的坐标为 $(a ， - a)$ ，点B坐标为 $(b ， c) ， a ， b ， c ，$ 满足 ${\begin{array}{l} 3 a - b + 2 c = 8 \\ a - 2 b - c = - 4 \end{array}$ ．
①若a没有平方根，判断点A在第几象限并说明理由；

②若点A到x轴的距离是点B到x轴距离的3倍，求点B的坐标．

查看试题解析
21. 如图，在△ABC中，AB=AC，点D、E、F分别在BC、AB、AC边上，且BE=CF，AD+EC=AB．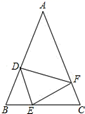

(1)、求证：△DEF是等腰三角形；

(2)、当∠A=40°时，求∠DEF的度数；

(3)、直接写出当∠A为多少度时，△DEF是等边三角形．

查看试题解析
22.

(1)、数轴上有A、B两点，若A点对应的数是﹣2，且A、B两点间的距离为3，则点B对应的数是；

(2)、已知线段AB=12cm，直线AB上有一点C，且BC=4cm，M是AC的中点，AM的长为；

(3)、已知∠AOB=3∠BOC，∠BOC=30°，则∠AOC=；

(4)、已知等腰三角形两边长为17、8，求三角形的周长．

查看试题解析

23. 中央电视台的“朗读者”节目激发了同学们的读书热情，为了引导学生“多读书，读好书”，某校对八年级部分学生的课外阅读量进行了随机调查，整理调查结果发现，学生课外阅读的本书最少的有5本，最多的有8本，并根据调查结果绘制了不完整的图表，如图所示：

本数（本）	频数（人数）	频率
5	$a$	0.2
6	18	0.36
7	14	$b$
8	8	0.16
合计	$c$	1

(1)、统计表中的a= ， b= ， c=；

(2)、请将频数分布表直方图补充完整；

(3)、求所有被调查学生课外阅读的平均本数；

(4)、若该校八年级共有1200名学生，请你分析该校八年级学生课外阅读7本及以上的人数.

查看试题解析

24. 唐山世园会期间，游乐场投资150万元引进一项大型游乐设施．若不计维修保养费用，预计开放后每月可创收31万元．而该游乐场开放后，从第1个月到第x个月的维修保养费用累计为y（万元），且y＝ax²＋bx．若将创收扣除投资和维修保养费用称为游乐场的纯收益g（万元），g也是关于x的二次函数．

(1)、若维修保养费用第1个月为2万元，第2个月为4万元，求y关于x的解析式；

(2)、求纯收益g关于x的解析式；

(3)、问设施开放几个月后，游乐场的纯收益达到最大？并求出最大收益．

查看试题解析
25. 如图1，在平面直角坐标系中，点O为坐标原点，点A（－1，0），点B（0， $\sqrt{3}$ ）．

(1)、求∠BAO的度数；

(2)、如图1，将△AOB绕点O顺时针旋转得△A′OB′，当点A′恰好落在AB边上时，设△AB′O的面积为S₁ ， △BA′O的面积为S₂ ， S₁与S₂有何关系？为什么？

(3)、若将△AOB绕点O顺时针旋转到如图2所示的位置，S₁与S₂的关系发生变化了吗？证明你的判断．

查看试题解析
26. 如图 $1$ ，矩形OABC的顶点A，C的坐标分别为（4，0），（0，6），直线AD交BC于点D．tan∠OAD=2，抛物线 $M_{1} ： y = a x^{2} + b x (a \neq 0)$ 过A，D两点．

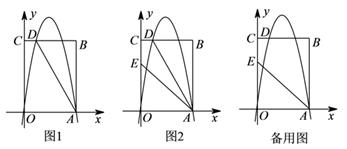(1)、求点D的坐标和抛物线M₁的表达式．

(2)、点P是抛物线M₁对称轴上一动点，当∠CPA=90°时，求所有满足条件的点P的坐标．

(3)、如图 $2$ ，点E（0，4），连接AE，将抛物线M₁的图象向下平移m（m>0）个单位得到抛物线M₂ ．

①设点D平移后的对应点为点D'，当点D'恰好落在直线AE上时，求m的值．

②当 $1 \leq x \leq m (m > 1)$ 时，若抛物线M₂与直线AE有两个交点，求m的取值范围．

查看试题解析