河北省石家庄市长安区2020年中考数学4月模拟试卷
试卷更新日期:2020-06-10 类型:中考模拟
一、单选题
-
1. 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
 A、
A、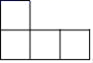 B、.
B、.  C、.
C、. 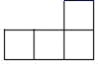 D、.
D、. 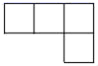 2. 第十三届全运会将于2017年8月在天津举行,其中足球项目承办场地为团泊足球场,该足球场占地163000平方米,将163000用科学记数法表示应为( )A、163×103 B、16.3×104 C、1.63×105 D、0.163×1063. 如图,在同一直角坐标系中,函数 与 的图象大致是( ).
2. 第十三届全运会将于2017年8月在天津举行,其中足球项目承办场地为团泊足球场,该足球场占地163000平方米,将163000用科学记数法表示应为( )A、163×103 B、16.3×104 C、1.63×105 D、0.163×1063. 如图,在同一直角坐标系中,函数 与 的图象大致是( ). A、①② B、①③ C、②④ D、③④4. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、5. 下列图形中,是中心对称图形的是( )A、
A、①② B、①③ C、②④ D、③④4. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、5. 下列图形中,是中心对称图形的是( )A、 B、
B、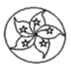 C、
C、 D、
D、 6. 计算2sin30°-2cos60°+tan45°的结果是( )A、2 B、 C、 D、17. 计算 的结果为( )A、 B、 C、 D、8. 抛物线y=﹣(x+2)2﹣3向右平移了3个单位,那么平移后抛物线的顶点坐标是( )A、(﹣5,﹣3) B、(﹣2,0) C、(﹣1,﹣3) D、(1,﹣3)9. 已知线段AB=8cm,在直线AB上画线BC,使它等于3cm,则线段AC等于( )A、11cm B、5cm C、11cm或5cm D、8cm或11cm10.
6. 计算2sin30°-2cos60°+tan45°的结果是( )A、2 B、 C、 D、17. 计算 的结果为( )A、 B、 C、 D、8. 抛物线y=﹣(x+2)2﹣3向右平移了3个单位,那么平移后抛物线的顶点坐标是( )A、(﹣5,﹣3) B、(﹣2,0) C、(﹣1,﹣3) D、(1,﹣3)9. 已知线段AB=8cm,在直线AB上画线BC,使它等于3cm,则线段AC等于( )A、11cm B、5cm C、11cm或5cm D、8cm或11cm10.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为( )
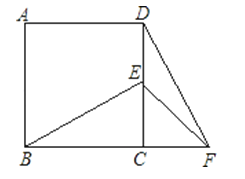 A、10° B、15° C、20° D、25°11. 如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于( )
A、10° B、15° C、20° D、25°11. 如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于( )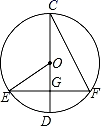 A、30° B、40° C、35° D、45°12. 已知抛物线y=x2-2mx-4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )A、(1,-5) B、(3,-13) C、(2,-8) D、(4,-20)
A、30° B、40° C、35° D、45°12. 已知抛物线y=x2-2mx-4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )A、(1,-5) B、(3,-13) C、(2,-8) D、(4,-20)二、填空题
-
13. 计算:3x2•5x3的结果为 .14. 已知点 与点 关于原点对称,则 .15. 如图,坡角为30°的斜坡上两树间的水平距离AC为2m,则两树间的坡面距离AB为
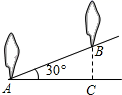 16. 若关于x、y的方程组 的解是 ,则mn的值为 .17. 如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF= EH,那么EH的长为 .
16. 若关于x、y的方程组 的解是 ,则mn的值为 .17. 如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF= EH,那么EH的长为 .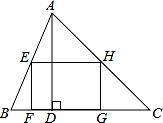 18. 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论:
18. 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论:①abc>0;
②方程ax2+bx+c=0的两根是x1=﹣1,x2=3;
③2a+b=0;
④4a2+2b+c<0,
其中正确结论的序号为 .

三、解答题
-
19. 解不等式组 请结合题意填空,完成本题的解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来:
 (4)、原不等式组的解集为 .20. 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)
(4)、原不等式组的解集为 .20. 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)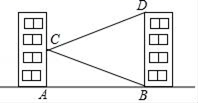 21. 如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.
21. 如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.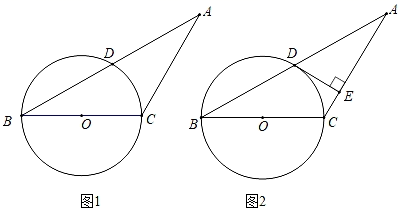 (1)、求证:点D是AB的中点;(2)、如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.22. 每年十月的第二个周四是世界爱眼日,为预防近视,超市决定对某型号护眼台灯进行降价销售.降价前,进价为30元的护眼台灯以80元售出,平均每月能售出200盏,调查表明:这种护眼台灯每盏售价每降低1元,其月平均销售量将增加10盏.(1)、写出月销售利润y(单位:元)与销售价x(单位:元/盏)之间的函数表达式;(2)、当销售价定为多少元时,所得月利润最大?最大月利润为多少元?23. 如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.
(1)、求证:点D是AB的中点;(2)、如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.22. 每年十月的第二个周四是世界爱眼日,为预防近视,超市决定对某型号护眼台灯进行降价销售.降价前,进价为30元的护眼台灯以80元售出,平均每月能售出200盏,调查表明:这种护眼台灯每盏售价每降低1元,其月平均销售量将增加10盏.(1)、写出月销售利润y(单位:元)与销售价x(单位:元/盏)之间的函数表达式;(2)、当销售价定为多少元时,所得月利润最大?最大月利润为多少元?23. 如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.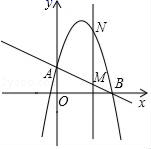 (1)、求该抛物线的解析式和顶点坐标;(2)、作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值,最大值是多少;(3)、在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标.(直接写出结果,不必写解答过程)24. 如图所示,在平面直角坐标系中A(0,2),点B(﹣3,0).△AOB绕点O逆时针旋转30°得到△A1OB1 .
(1)、求该抛物线的解析式和顶点坐标;(2)、作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值,最大值是多少;(3)、在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标.(直接写出结果,不必写解答过程)24. 如图所示,在平面直角坐标系中A(0,2),点B(﹣3,0).△AOB绕点O逆时针旋转30°得到△A1OB1 .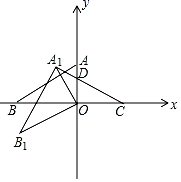 (1)、直接写出点B1的坐标;(2)、点C(2,0),连接CA1交OA于点D,求点D的坐标.
(1)、直接写出点B1的坐标;(2)、点C(2,0),连接CA1交OA于点D,求点D的坐标.