河北省沙河市2020年中考数学模拟试卷
试卷更新日期:2020-06-10 类型:中考模拟
一、单选题
-
1. 我们知道,平面内不垂直的两条相交直线是轴对称图形,该图形对称轴条数为( )A、1 B、2 C、4 D、无数2. 图中的三视图所对应的几何体是( )
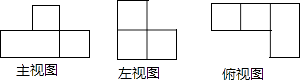 A、
A、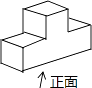 B、
B、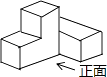 C、
C、 D、
D、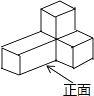 3. 冠状病毒颗粒的直径60~200nm,平均直径为100nm,新型冠状病毒直径为178nm,呈球形或椭圆形,具有多形性.如果 米,那么新型冠状病毒的半径约为( )米。A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,问木长多少尺,设木长为 尺,绳子长为 尺,则下列正确的方程组是( )A、 B、 C、 D、6. 用尺规作图,已知三边作三角形,用到的基本作图是( )A、作一个角等于已知角 B、作一条线段等于已知线段 C、作已知直线的垂线 D、作角的平分线7. 嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km (最小圆的半径是1km ),下列关于小艇 A , B 的位置描述,正确的是( )
3. 冠状病毒颗粒的直径60~200nm,平均直径为100nm,新型冠状病毒直径为178nm,呈球形或椭圆形,具有多形性.如果 米,那么新型冠状病毒的半径约为( )米。A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,问木长多少尺,设木长为 尺,绳子长为 尺,则下列正确的方程组是( )A、 B、 C、 D、6. 用尺规作图,已知三边作三角形,用到的基本作图是( )A、作一个角等于已知角 B、作一条线段等于已知线段 C、作已知直线的垂线 D、作角的平分线7. 嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km (最小圆的半径是1km ),下列关于小艇 A , B 的位置描述,正确的是( )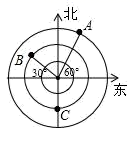 A、小艇 A 在游船的北偏东60°方向上,且与游船的距离是3km B、游船在小艇A的南偏西60°方向上,且与小艇 A 的距离是3km C、小艇 B 在游船的北偏西30°方向上,且与游船的距离是 2km D、游船在小艇 B 的南偏东60°方向上,且与小艇 B 的距离是 2km8. 如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
A、小艇 A 在游船的北偏东60°方向上,且与游船的距离是3km B、游船在小艇A的南偏西60°方向上,且与小艇 A 的距离是3km C、小艇 B 在游船的北偏西30°方向上,且与游船的距离是 2km D、游船在小艇 B 的南偏东60°方向上,且与小艇 B 的距离是 2km8. 如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.
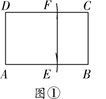
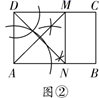
对于以上两种作法,可以做出的判定是( )
A、甲正确,乙不正确 B、甲、乙均正确 C、乙正确,甲不正确 D、甲、乙均不正确9. 五个整数从小到大排列,中位数是4,如果这组数据唯一的众数是6,则这五个整数的和的最大值可能是( )A、17 B、19 C、21 D、2210. 小组活动中,同学们采用接力的方式求一元一次方程的解,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后求出方程的解.过程如下: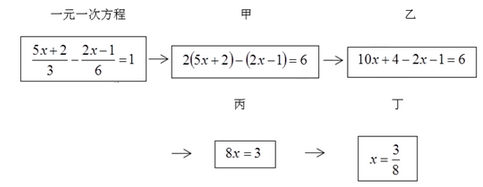
接力中,自己负责的一步出现错误的是( )
A、甲 B、乙 C、丙 D、丁11. 在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )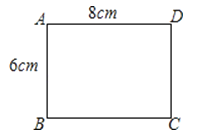 A、1 B、2 C、3 D、412. 老王面前有两个容积相同的杯子,杯子甲他装了三分之一的葡萄酒,杯子乙他装了半杯的王老吉凉茶,老张过来将装有凉茶的杯子乙倒满了酒,老王又将杯子乙中饮料倒一部分到杯子甲,使得两个杯子的饮料分量相同.然后老王让老张先选一杯一起喝了,如果老张不想多喝酒,那么他应该选择( )A、甲杯 B、乙杯 C、甲、乙是一样的 D、无法确定13. 如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )
A、1 B、2 C、3 D、412. 老王面前有两个容积相同的杯子,杯子甲他装了三分之一的葡萄酒,杯子乙他装了半杯的王老吉凉茶,老张过来将装有凉茶的杯子乙倒满了酒,老王又将杯子乙中饮料倒一部分到杯子甲,使得两个杯子的饮料分量相同.然后老王让老张先选一杯一起喝了,如果老张不想多喝酒,那么他应该选择( )A、甲杯 B、乙杯 C、甲、乙是一样的 D、无法确定13. 如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )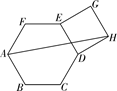 A、3 B、 C、2 D、14. 已知 ,则 的值为( )A、5 B、10 C、32 D、6415. 如图,在 中, , . , 是 的内心,则线段 的值为( )
A、3 B、 C、2 D、14. 已知 ,则 的值为( )A、5 B、10 C、32 D、6415. 如图,在 中, , . , 是 的内心,则线段 的值为( )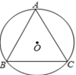 A、 B、 C、 D、16. 欧几里得在《几何原本》中,记载了用图解法解方程 的方法,类似地可以用折纸的方法求方程 的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片 ,先折出 的中点 ,再折出线段 ,然后通过折叠使 落在线段 上,折出点 的新位置 ,因而 ,类似地,在 上折出点 使 。此时, 的长度可以用来表示方程 的一个正根;乙:如图2,裁一张边长为1的正方形的纸片 ,先折出 的中点 ,再折出线段 N,然后通过沿线段 折叠使 落在线段 上,折出点 的新位置 ,因而 。此时, 的长度可以用来表示方程 的一个正根;甲、乙两人的做法和结果( )。
A、 B、 C、 D、16. 欧几里得在《几何原本》中,记载了用图解法解方程 的方法,类似地可以用折纸的方法求方程 的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片 ,先折出 的中点 ,再折出线段 ,然后通过折叠使 落在线段 上,折出点 的新位置 ,因而 ,类似地,在 上折出点 使 。此时, 的长度可以用来表示方程 的一个正根;乙:如图2,裁一张边长为1的正方形的纸片 ,先折出 的中点 ,再折出线段 N,然后通过沿线段 折叠使 落在线段 上,折出点 的新位置 ,因而 。此时, 的长度可以用来表示方程 的一个正根;甲、乙两人的做法和结果( )。
 A、甲对,乙错 B、乙对,甲错 C、甲乙都对 D、甲乙都错
A、甲对,乙错 B、乙对,甲错 C、甲乙都对 D、甲乙都错二、填空题
-
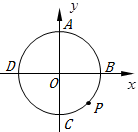
17. 一个长方形的长和宽分别为 和 ,则这个长方形的面积为.18. 已知a+1=20002+20022 , 计算 = .19. 如图,半径为 且坐标原点为圆心的圆交 轴、 轴于点 、 、 、 ,过圆上的一动点 (不与 重合)作 ,且 在 右侧)
⑴连结 ,当 时,则点 的横坐标是 .
⑵连结 ,设线段 的长为 ,则 的取值范围是 .
三、解答题
-
20. 已知 , ,且化简2A-B的结果与 无关.(1)、求m、n的值;(2)、求式子 的值.21. 图1为奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为 ,其它四个数分别记为 (如图2);图3为按某一规律排成的另一个数表,用十字框任意框出5个数,记框内中间这个数为 ,其它四个数记为 (如图4).
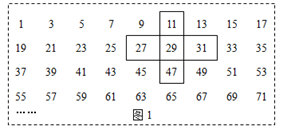
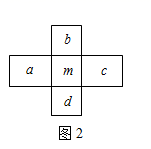
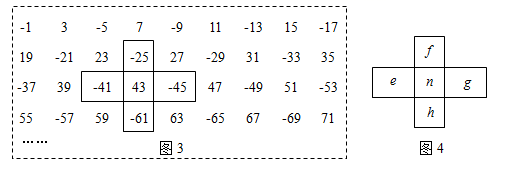 (1)、请用含m的代数式表示b.(2)、请用含n的代数式表示e.(3)、若a+b+c+d=km,e+f+g+h+pn,求k+3p的值.22. 某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
(1)、请用含m的代数式表示b.(2)、请用含n的代数式表示e.(3)、若a+b+c+d=km,e+f+g+h+pn,求k+3p的值.22. 某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:a.七年级成绩频数分布直方图:
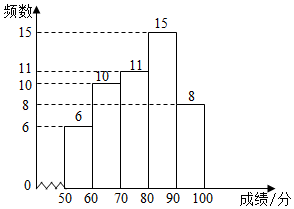
b.七年级成绩在 这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级
平均数
中位数
七
76.9
m
八
79.2
79.5
根据以上信息,回答下列问题:
(1)、在这次测试中,七年级在80分以上(含80分)的有人;(2)、表中m的值为;(3)、在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;(4)、该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.23. 已知正方形 的边长为4,一个以点 为顶点的 角绕点 旋转,角的两边分别与边 的延长线交于点 ,连接 ,设 .(1)、如图1,当 被对角线 平分时,求 的值;

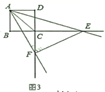 (2)、求证: 与 相似;(3)、当 的外心在其边上时,求 的值.24. 某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程 (米)与时间 (分)的函数关系如图2所示.
(2)、求证: 与 相似;(3)、当 的外心在其边上时,求 的值.24. 某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程 (米)与时间 (分)的函数关系如图2所示.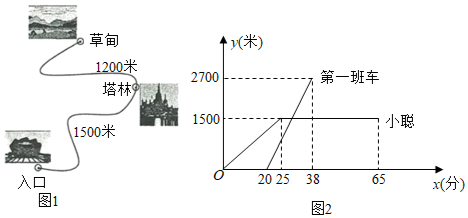 (1)、求第一班车离入口处的路程y(米)与时间x(分)的函数表达式.(2)、求第一班车从人口处到达塔林所蓄的时间.(3)、小聪在塔林游玩40分钟后,想坐班车到草甸,则小聘聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)25. 如图,在 中, , 于 ,且 .点 从点 出发,沿 方向匀速运动,速度为 ;同时直线 由点 出发沿 方向匀速运动,速度为 ,运动过程中始终保持 ,直线 交 于 ,交 于 ,连接 ,设运动时间为 .
(1)、求第一班车离入口处的路程y(米)与时间x(分)的函数表达式.(2)、求第一班车从人口处到达塔林所蓄的时间.(3)、小聪在塔林游玩40分钟后,想坐班车到草甸,则小聘聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)25. 如图,在 中, , 于 ,且 .点 从点 出发,沿 方向匀速运动,速度为 ;同时直线 由点 出发沿 方向匀速运动,速度为 ,运动过程中始终保持 ,直线 交 于 ,交 于 ,连接 ,设运动时间为 .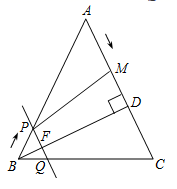 (1)、 , , ;(用含 的式子表示)(2)、当四边形 是平行四边形时,求 的值;(3)、当点 在线段 的垂直平分线上时,求 的值;(4)、是否存在时刻 ,使以 为直径的圆与 的边相切?若存在,直接写出 的值;若不存在,请说明理由.26. 把函数 的图象绕点 旋转 ,得到新函数 的图象,我们称 是 关于点 的相关函数. 的图象的对称轴与 轴交点坐标为 .(1)、填空: 的值为(用含 的代数式表示)(2)、若 ,当 时,函数 的最大值为 ,最小值为 ,且 ,求 的解析式;(3)、当 时, 的图象与 轴相交于 两点(点 在点 的右侧).与 轴相交于点 .把线段 原点 逆时针旋转 ,得到它的对应线段 ,若线 与 的图象有公共点,结合函数图象,求 的取值范围.
(1)、 , , ;(用含 的式子表示)(2)、当四边形 是平行四边形时,求 的值;(3)、当点 在线段 的垂直平分线上时,求 的值;(4)、是否存在时刻 ,使以 为直径的圆与 的边相切?若存在,直接写出 的值;若不存在,请说明理由.26. 把函数 的图象绕点 旋转 ,得到新函数 的图象,我们称 是 关于点 的相关函数. 的图象的对称轴与 轴交点坐标为 .(1)、填空: 的值为(用含 的代数式表示)(2)、若 ,当 时,函数 的最大值为 ,最小值为 ,且 ,求 的解析式;(3)、当 时, 的图象与 轴相交于 两点(点 在点 的右侧).与 轴相交于点 .把线段 原点 逆时针旋转 ,得到它的对应线段 ,若线 与 的图象有公共点,结合函数图象,求 的取值范围.