北京理工附中2020年中考数学三模试卷
试卷更新日期:2020-06-10 类型:中考模拟
一、单选题
-
1. 2019年10月1日,约120 000名群众观看了天安门广场的升旗仪式.将120 000用科学记数法表示应为( )A、 B、 C、 D、2. 下列四个图形依次是北京、云南、西藏、安徽四个省市的图案字体,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 六边形的外角和是 ( )A、360° B、540° C、720° D、900°4. 下列几何体中,主视图和左视图完全相同的图形的有几个 ( )
3. 六边形的外角和是 ( )A、360° B、540° C、720° D、900°4. 下列几何体中,主视图和左视图完全相同的图形的有几个 ( ) A、1个 B、2个 C、3个 D、4个5. 用配方法解方程 ,配方后的方程是 ( )A、 B、 C、 D、6. 如图,直线 直线 分别与 , 交于点 , , ,且与 的平分线交于 ,若 ,则 的度数是( )
A、1个 B、2个 C、3个 D、4个5. 用配方法解方程 ,配方后的方程是 ( )A、 B、 C、 D、6. 如图,直线 直线 分别与 , 交于点 , , ,且与 的平分线交于 ,若 ,则 的度数是( )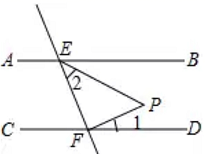 A、35° B、30° C、55° D、20°7. 二十四节气是中国古代劳动人民长期经验积累的结品,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.下图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长超过14小时的节气是( )
A、35° B、30° C、55° D、20°7. 二十四节气是中国古代劳动人民长期经验积累的结品,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.下图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长超过14小时的节气是( )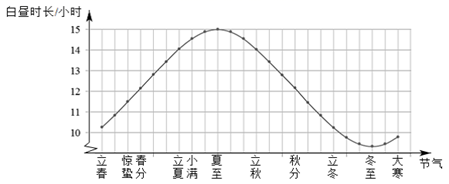 A、惊蛰 B、立夏 C、夏至 D、大寒8. 图1是2020年3月26日全国新冠疫情数据表,图2是3月28日海外各国疫情统计表,图3是中国和海外的病死率趋势对比图,根据这些图表,选出下列说法中错误的一项( )
A、惊蛰 B、立夏 C、夏至 D、大寒8. 图1是2020年3月26日全国新冠疫情数据表,图2是3月28日海外各国疫情统计表,图3是中国和海外的病死率趋势对比图,根据这些图表,选出下列说法中错误的一项( )

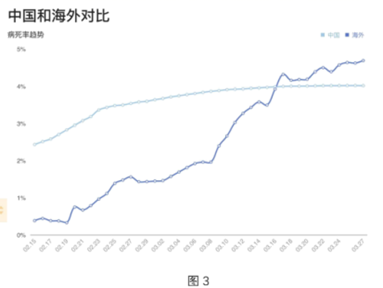 A、图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量. B、图2显示美国累计确诊人数虽然约是德国的两倍,但每百万人口的确诊人数大约只有德国的一半. C、图2显示意大利当前的治愈率高于西班牙. D、图3显示大约从3月16日开始海外的病死率开始高于中国的病死率
A、图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量. B、图2显示美国累计确诊人数虽然约是德国的两倍,但每百万人口的确诊人数大约只有德国的一半. C、图2显示意大利当前的治愈率高于西班牙. D、图3显示大约从3月16日开始海外的病死率开始高于中国的病死率二、填空题
-
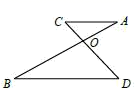
9. 分解因式: .10. 在平面直角坐标系 中,将点 绕原点 顺时针旋转90°,所得到的对应点的坐标为 .11. 已知函数满足下列两个条件:①当 时, 随 的增大而减小;②它的图象经过坐标原点,请写出一个符合上述条件的函数的表达式 .12. 如图, , 相交于 点, , , ,则 的长为 .
 13. 如图,在平面直角坐标系 中, , ,双曲线 与线段 无公共点,则 的取值范围是 .
13. 如图,在平面直角坐标系 中, , ,双曲线 与线段 无公共点,则 的取值范围是 .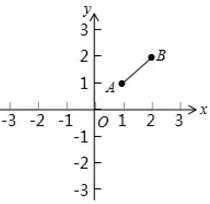 14. 在数学课上,老师提出如下问题:
14. 在数学课上,老师提出如下问题:尺规作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小云的作法如下:
⑴在直线l上任取一点B;
⑵以B为圆心,BA长为半径作弧,交直线l于点C;
⑶分别以A,C为圆心,BA长为半径作弧,两弧相交于点D;
⑷作直线AD.直线AD即为所求.
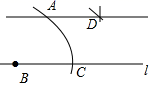
小云作图的依据是 .
15. 某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.商品
顾客人数
甲
乙
丙
丁
100
√
×
√
√
217
×
√
×
√
200
√
√
√
×
300
√
×
√
×
85
√
×
×
×
98
×
√
×
×
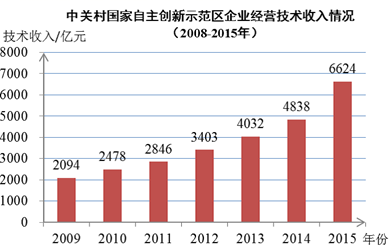
(1)、估计顾客同时购买乙和丙的概率为 .(2)、如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买(填乙、丙、丁)商品的可能性最大.16. 上图为2009年到2015年中关村国家自主创新示范区企业经营技术收入的统计图.下面四个推断:
①2009年到2015年技术收入持续增长;
②2009年到2015年技术收入的中位数是3403亿;
③2009年到2015年技术收入增幅最大的是2015年;
④2009年到2011年的技术收入平均增长率比2013年到2015年技术收入平均增长率大.
其中,正确的是 .
三、解答题
-
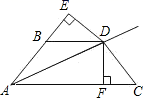
17. 计算:18. 先化简: ,再从 的整数中选取一个你喜欢的 的值代入求值.19. 如图所示, 是 的平分线, ,垂足为 , ,垂足为 ,且 .
求证: .
 20. 已知关于 的方程 .(1)、若该方程有两个不相等的实数根,求实数 的取值范围:(2)、当该方程的一个根为-3时,求 的值及方程的另一根.21. 如图,在矩形 中,对角线 的垂直平分线 与 相交于点 ,与 相交于点 .连接 , .
20. 已知关于 的方程 .(1)、若该方程有两个不相等的实数根,求实数 的取值范围:(2)、当该方程的一个根为-3时,求 的值及方程的另一根.21. 如图,在矩形 中,对角线 的垂直平分线 与 相交于点 ,与 相交于点 .连接 , .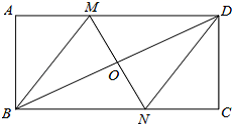 (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.22. 小辉为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.22. 小辉为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.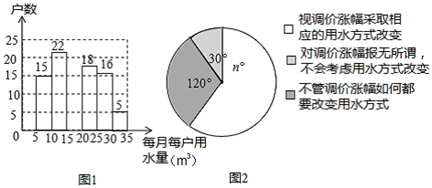
小辉发现每月每户的用水量在 之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变.根据小军绘制的图表和发现的信息,完成下列问题:
(1)、 , 小明调查了户居民,并补全图1;(2)、每月每户用水量的中位数落在之间,众数落在之间;(3)、如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数多少?23. 如图,已知 ,以 为直径的 交 于点 ,点 为弧 的中点,连接 交 于点 .且 .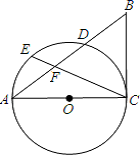 (1)、求证: 是 的切线;(2)、若 的半径为4, ,求 的长.24. 在平面直角坐标系 中,函数 ( )的图象 经过点 (4,1),直线 与图象 交于点 ,与 轴交于点 .(1)、求 的值;(2)、横、纵坐标都是整数的点叫做整点.记图象 在点 , 之间的部分与线段 , , 围成的区域(不含边界)为 .
(1)、求证: 是 的切线;(2)、若 的半径为4, ,求 的长.24. 在平面直角坐标系 中,函数 ( )的图象 经过点 (4,1),直线 与图象 交于点 ,与 轴交于点 .(1)、求 的值;(2)、横、纵坐标都是整数的点叫做整点.记图象 在点 , 之间的部分与线段 , , 围成的区域(不含边界)为 .①当 时,直接写出区域 内的整点个数;
②若区域 内恰有4个整点,结合函数图象,求 的取值范围.
25. 如图,在 中, , 于点 , ,为了研究图中线段之间的关系,设 , ,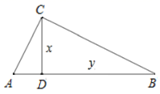 (1)、可通过证明 ,得到 关于 的函数表达式 , 其中自变量 的取值范围是;(2)、根据图中给出的(1)中函数图象上的点,画出该函数的图象;
(1)、可通过证明 ,得到 关于 的函数表达式 , 其中自变量 的取值范围是;(2)、根据图中给出的(1)中函数图象上的点,画出该函数的图象;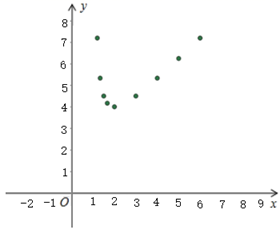 (3)、借助函数图象,回答下列问题:① 的最小值是;②已知当 时, 的形状与大小唯一确定,借助函数图象给出 的一个估计值(精确到0.1)或者借助计算给出 的精确值.26. 在平面直角坐标系 中,抛物线 与 交于点 ,将点 向右平移某个距离得到点 ,点 在抛物线上.已知点 , .(1)、当 时.
(3)、借助函数图象,回答下列问题:① 的最小值是;②已知当 时, 的形状与大小唯一确定,借助函数图象给出 的一个估计值(精确到0.1)或者借助计算给出 的精确值.26. 在平面直角坐标系 中,抛物线 与 交于点 ,将点 向右平移某个距离得到点 ,点 在抛物线上.已知点 , .(1)、当 时.①求点 的坐标(用含 的式子表示);
②求线段 的长度;
(2)、若抛物线与线段 恰有一个公共点,结合函数图象,求 的取值范围.27. 如图, 中, . .将 绕点 顺时针旋转60°到点 ,点 与点 关于直线 对称,连接 , , .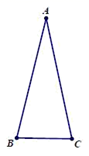 (1)、依题意补全图形:(2)、判断 的形状,并证明你的结论;(3)、请问在直线 上是否存在点 .使得 恒成立若存在,请用文字描述出点 的准确位置,并画图证明;若不存在,请说明理由.28. 对于平面内的点 和点 ,给出如下定义:点 为平面内一点,若点 使得 是以 为顶角且 小于90°的等腰三角形,则称点 是点 关于点 的锐角等腰点.如图,点 是点 关于点 的锐角等腰点.
(1)、依题意补全图形:(2)、判断 的形状,并证明你的结论;(3)、请问在直线 上是否存在点 .使得 恒成立若存在,请用文字描述出点 的准确位置,并画图证明;若不存在,请说明理由.28. 对于平面内的点 和点 ,给出如下定义:点 为平面内一点,若点 使得 是以 为顶角且 小于90°的等腰三角形,则称点 是点 关于点 的锐角等腰点.如图,点 是点 关于点 的锐角等腰点.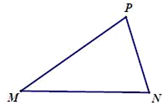
在平面直角坐标系xOy中,点O为坐标原点
(1)、已知点 ,在点 , , , 中,是点 关于点 的锐角等腰点的是;(2)、已知点 ,点 在直线 上,若点 是点 关于点 的锐角等腰点,求实数 的取值范围.(3)、点 是 轴上的动点, , ,点 是以点 为圆心,2为半径的圆上一动点.且满足 ,若直线 上存在点 关于点 的锐角等腰点,请直接写出 的取值范围.