安徽省宿州市2020年中考数学4月模拟试卷
试卷更新日期:2020-06-10 类型:中考模拟
一、单选题
-
1. 一个数的相反数是它本身,则这个数为( )A、0 B、1 C、﹣1 D、±12. 下列运算正确的是( )A、a12÷a6=a6 B、(a﹣2b)2=a﹣4b C、a3•a3=2a6 D、(a2)3=a53. 下列几何体中,从正面看(主视图)是长方形的是( )A、
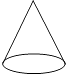 B、
B、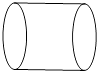 C、
C、 D、
D、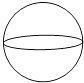 4. 截止到 2019 年 9 月 3 日,电影《哪吒之魔童降世》的累计票房达到 47.24 亿,47.24 亿用科学记数法表示为( )A、 B、 C、 D、5. 解分式方程 时,去分母化为一元一次方程,正确的是( )A、x+1=2(x﹣1) B、x﹣1=2(x+1) C、x﹣1=2 D、x+1=26. 如图,正方形OABC的边长为6,D为AB中点,OB交CD于点Q,Q是y= 上一点,k的值是( )
4. 截止到 2019 年 9 月 3 日,电影《哪吒之魔童降世》的累计票房达到 47.24 亿,47.24 亿用科学记数法表示为( )A、 B、 C、 D、5. 解分式方程 时,去分母化为一元一次方程,正确的是( )A、x+1=2(x﹣1) B、x﹣1=2(x+1) C、x﹣1=2 D、x+1=26. 如图,正方形OABC的边长为6,D为AB中点,OB交CD于点Q,Q是y= 上一点,k的值是( )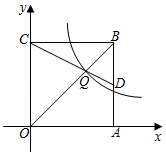 A、4 B、8 C、16 D、247. 肆虐的冠状病毒肺炎具有人传人性,调查发现:1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,依题意可列方程( )A、1+x=225 B、1+x2=225 C、(1+x)2=225 D、1+(1+x2 )=2258. 如图,王虎使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2 , 其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A、4 B、8 C、16 D、247. 肆虐的冠状病毒肺炎具有人传人性,调查发现:1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,依题意可列方程( )A、1+x=225 B、1+x2=225 C、(1+x)2=225 D、1+(1+x2 )=2258. 如图,王虎使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2 , 其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( ) A、10cm B、4πcm C、 D、9. 如果分式方程 无解,则 的值为( )A、-4 B、 C、2 D、-210. 在正方形ABCD中,点E为BC边的中点,点F在对角线AC上,连接FB、FE.当点F在AC上运动时,设AF=x,△BEF的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
A、10cm B、4πcm C、 D、9. 如果分式方程 无解,则 的值为( )A、-4 B、 C、2 D、-210. 在正方形ABCD中,点E为BC边的中点,点F在对角线AC上,连接FB、FE.当点F在AC上运动时,设AF=x,△BEF的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )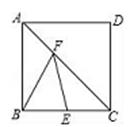 A、
A、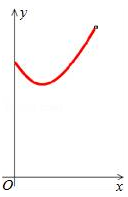 B、
B、 C、
C、 D、
D、
二、填空题
-
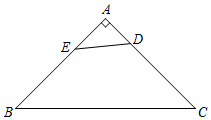
11. 分解因式6xy2-9x2y-y3 = .12. 已知,实数 满足 ,求代数式 的值等于 .13. 如图,在等腰直角△ABC中,AB=4,点D是边AC上一点,且AD=1,点E是AB边上一点,连接DE , 以线段DE为直角边作等腰直角△DEF(D、E、F三点依次呈逆时针方向),当点F恰好落在BC边上时,则AE的长是 .
 14. 如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AM•AD;③MN=3- ;④S△EBC=2 -1,其中正确的结论是(把你认为正确结论的序号都填上).
14. 如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AM•AD;③MN=3- ;④S△EBC=2 -1,其中正确的结论是(把你认为正确结论的序号都填上).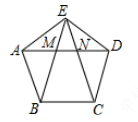
三、解答题
-
15. 计算: .16. 现有学生若干人,分住若干宿舍.如果每间住4人,那么还余20人;如果每间住6人,那么有一间宿舍只住了2人.试求学生人数和宿舍间数.17. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
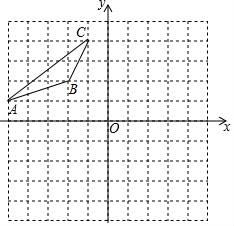 (1)、将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1 , 画出△A1B1C1;(2)、画出与△ABC关于原点O成中心对称的△A2B2C2 , 并直接写出点A2的坐标.18. 记:P1=﹣2,P2=(﹣2)×(﹣2),P3=(﹣2)×(﹣2)×(﹣2),…, .(1)、计算P7÷P8的值;(2)、计算2P2019+P2020的值;(3)、猜想2Pn与Pn+1的关系,并说明理由.19. 如图,从A城市到B城市要翻过一座大山,现需要打通隧道,修建高铁方便两地出行,已知在A城市的北偏东30°方向和B城市的北偏西67°方向有一C地,A , C相距230km , 求A , B两个城市之间的距离.(参考数据:sin67°≈ ,cos67°≈ ,tan67°≈ , ≈1.7,结果精确到1km)
(1)、将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1 , 画出△A1B1C1;(2)、画出与△ABC关于原点O成中心对称的△A2B2C2 , 并直接写出点A2的坐标.18. 记:P1=﹣2,P2=(﹣2)×(﹣2),P3=(﹣2)×(﹣2)×(﹣2),…, .(1)、计算P7÷P8的值;(2)、计算2P2019+P2020的值;(3)、猜想2Pn与Pn+1的关系,并说明理由.19. 如图,从A城市到B城市要翻过一座大山,现需要打通隧道,修建高铁方便两地出行,已知在A城市的北偏东30°方向和B城市的北偏西67°方向有一C地,A , C相距230km , 求A , B两个城市之间的距离.(参考数据:sin67°≈ ,cos67°≈ ,tan67°≈ , ≈1.7,结果精确到1km)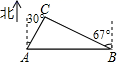 20. 某中学准备举办一次演讲比赛,每班限定两人报名,初三(1)班的三位同学(两位女生,一位男生)都想报名参加,班主任李老师设计了一个摸球游戏,利用已学过的概率知识来决定谁去参加比赛,游戏规则如下:在一个不透明的箱子里放3个大小质地完全相同的乒乓球,在这3个乒乓球上分别写上 、 、 (每个字母分别代表一位同学,其中 、 分别代表两位女生, 代表男生),搅匀后,李老师从箱子里随机摸出一个乒乓球,不放回,再次搅匀后随机摸出第二个乒乓球,根据乒乓球上的字母决定谁去参加比赛。(1)、求李老师第一次摸出的乒乓球代表男生的概率;(2)、请用列表或画树状图的方法求恰好选定一名男生和一名女生参赛的概率.21. 如图所示,在同一直角坐标系xOy中,有双曲线 ,直线y2=k2x+b1 , y3=k3x+b2 , 且点A(2,5),点B(﹣6,n)在双曲线的图象上
20. 某中学准备举办一次演讲比赛,每班限定两人报名,初三(1)班的三位同学(两位女生,一位男生)都想报名参加,班主任李老师设计了一个摸球游戏,利用已学过的概率知识来决定谁去参加比赛,游戏规则如下:在一个不透明的箱子里放3个大小质地完全相同的乒乓球,在这3个乒乓球上分别写上 、 、 (每个字母分别代表一位同学,其中 、 分别代表两位女生, 代表男生),搅匀后,李老师从箱子里随机摸出一个乒乓球,不放回,再次搅匀后随机摸出第二个乒乓球,根据乒乓球上的字母决定谁去参加比赛。(1)、求李老师第一次摸出的乒乓球代表男生的概率;(2)、请用列表或画树状图的方法求恰好选定一名男生和一名女生参赛的概率.21. 如图所示,在同一直角坐标系xOy中,有双曲线 ,直线y2=k2x+b1 , y3=k3x+b2 , 且点A(2,5),点B(﹣6,n)在双曲线的图象上 (1)、求y1和y2的解析式;(2)、若y3与直线x=4交于双曲线,且y3∥y2 , 求y3的解析式;(3)、直接写出 的解集.22. 如图,AB是⊙O的直径, ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
(1)、求y1和y2的解析式;(2)、若y3与直线x=4交于双曲线,且y3∥y2 , 求y3的解析式;(3)、直接写出 的解集.22. 如图,AB是⊙O的直径, ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF. (1)、求证:直线BF是⊙O的切线;(2)、若OB=2,求BD的长.23. 如图,已知直线 与 轴和 轴分别交于点 和点 抛物线 经过点 与直线 的另一个交点为 .
(1)、求证:直线BF是⊙O的切线;(2)、若OB=2,求BD的长.23. 如图,已知直线 与 轴和 轴分别交于点 和点 抛物线 经过点 与直线 的另一个交点为 .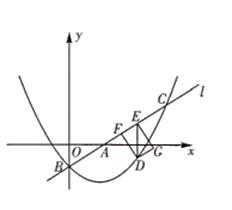 (1)、求 的值和抛物线的解析式(2)、点 在抛物线上, 轴交直线 于点 点 在直线 上,且四边形 为矩形.设点 的横坐标为 矩形 的周长为 求 与 的函数关系式以及 的最大值(3)、将 绕平面内某点 逆时针旋转 得到 (点 分别与 点对应),若 的两个顶点恰好落在抛物线上,请直接写出点 的坐标.
(1)、求 的值和抛物线的解析式(2)、点 在抛物线上, 轴交直线 于点 点 在直线 上,且四边形 为矩形.设点 的横坐标为 矩形 的周长为 求 与 的函数关系式以及 的最大值(3)、将 绕平面内某点 逆时针旋转 得到 (点 分别与 点对应),若 的两个顶点恰好落在抛物线上,请直接写出点 的坐标.