安徽省芜湖市2020年中考数学一模试卷
试卷更新日期:2020-06-10 类型:中考模拟
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、 C、 D、2. 下列运算正确的是( )A、(﹣a3)2=﹣a6 B、2a2+3a2=6a2 C、2a2•a3=2a6 D、3. 如图所示的几何体的左视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、5. 一次抽奖活动特等奖的中奖率为 ,把 用科学记数法表示为( )A、 B、 C、 D、6. 尺规作图要求:I、过直线外一点作这条直线的垂线:II、作线段的垂直平分线;III、过直线上一点作这条直线的垂线: IV、 作角的平分线.如图是按上述要求排乱顺序的尺规作图:
4. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、5. 一次抽奖活动特等奖的中奖率为 ,把 用科学记数法表示为( )A、 B、 C、 D、6. 尺规作图要求:I、过直线外一点作这条直线的垂线:II、作线段的垂直平分线;III、过直线上一点作这条直线的垂线: IV、 作角的平分线.如图是按上述要求排乱顺序的尺规作图:
则正确的配对是( )
A、①-IV,②-II,③-I,④-III B、①-IV, ②-I,③-II,④-I C、①-II,②-IV,③-1II,④-I D、①-IV,②-I,③-II,④-III7. 《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问若每日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34 685个字,设他第一天读x个字,则下面所列方程正确的是( ).A、x+2x+4x=34 685 B、x+2x+3x=34 685 C、x+2x+2x=34 685 D、x+ x+ x=34 6858. 如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( ) A、4.5 B、4 C、3 D、29. 已知 是非零实数, ,在同一平面直角坐标系中,二次函数 与一次函数 的大致图象不可能是( )A、
A、4.5 B、4 C、3 D、29. 已知 是非零实数, ,在同一平面直角坐标系中,二次函数 与一次函数 的大致图象不可能是( )A、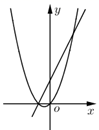 B、
B、 C、
C、 D、
D、 10. 如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E , D是线段BE上的一个动点,则 的最小值是( )
10. 如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E , D是线段BE上的一个动点,则 的最小值是( )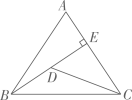 A、 B、 C、 D、10
A、 B、 C、 D、10二、填空题
-
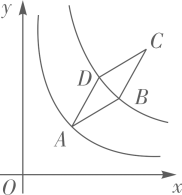
11. 因式分解: .12. 函数 中自变量x的取值范围是.13. 如图,菱形ABCD顶点A在例函数y= (x>0)的图象上,函数 y= (k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠DAB=30°,则k的值为.
 14. 如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为 .
14. 如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为 .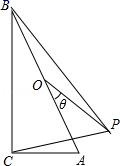
三、解答题
-
15. 计算: .16. 如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).
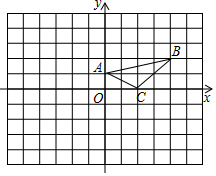 (1)、将△ABC沿y轴翻折得到△A1B1C1 , 画出△A1B1C1;(2)、将△ABC绕着点(﹣1,﹣1)旋转180°得到△A2B2C2 , 画出△A2B2C2;(3)、线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为 .17. 如图,已知直线 ,直线 , 与 相交于点 , , 分别与 轴相交于点 .
(1)、将△ABC沿y轴翻折得到△A1B1C1 , 画出△A1B1C1;(2)、将△ABC绕着点(﹣1,﹣1)旋转180°得到△A2B2C2 , 画出△A2B2C2;(3)、线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为 .17. 如图,已知直线 ,直线 , 与 相交于点 , , 分别与 轴相交于点 .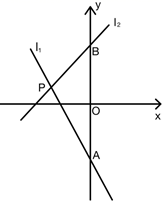 (1)、求点P的坐标.(2)、若 ,求x的取值范围.(3)、点 为x轴上的一个动点,过 作x轴的垂线分别交 和 于点 ,当EF=3时,求m的值.18. 某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)、求点P的坐标.(2)、若 ,求x的取值范围.(3)、点 为x轴上的一个动点,过 作x轴的垂线分别交 和 于点 ,当EF=3时,求m的值.18. 某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)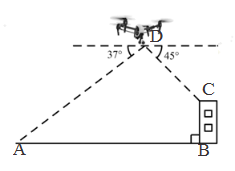
19. 如图, 是 的直径, 是圆周上的点, ,弦 交 于点 . (1)、求证:(2)、若 求 的度数.20. 学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图1,2).请根据统计图解答下列问题:
(1)、求证:(2)、若 求 的度数.20. 学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图1,2).请根据统计图解答下列问题: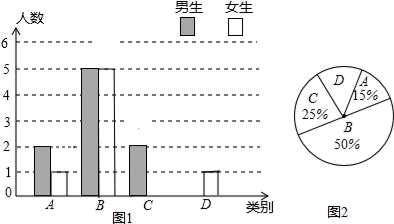 (1)、本次调查中,王老师一共调查了名学生;(2)、将条形统计图补充完整;(3)、为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.21. 观察下列数据:
(1)、本次调查中,王老师一共调查了名学生;(2)、将条形统计图补充完整;(3)、为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.21. 观察下列数据:
请回答:
(1)、第1行所有数字之和为(用含字母n的式子表示);(2)、表格中所有数字之和为(用含字母n的式子表示);(3)、根据以上的信息,计算 =22. 国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A、B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元;花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同.(1)、求A,B两种型号汽车的进货单价;(2)、销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系yB=﹣x+14,A型汽车的售价比B型汽车的售价高2万元/台.问A、B两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?23.(1)、问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
① 的值为;
②∠AMB的度数为 .
(2)、类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断 的值及∠AMB的度数,并说明理由;
(3)、拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB= ,请直接写出当点C与点M重合时AC的长.