安徽省豪州涡阳县2020年中考数学二模试卷

试卷更新日期：2020-06-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 化简 ${(- x^{3})}^{2}$ 的结果是（　　）

A、 $- x^{6}$ B、 $- x^{5}$ C、 $x^{6}$ D、 $x^{5}$

查看试题解析
2. 下列抛物线中，顶点坐标为 $(2, 1)$ 的是（　　）

A、 $y = {(x + 2)}^{2} + 1$ B、 $y = {(x - 2)}^{2} + 1$ C、 $y = {(x + 2)}^{2} - 1$ D、 $y = {(x - 2)}^{2} - 1$

查看试题解析
3. 在Rt△ABC中，∠C＝90°，如果∠A＝α，AB＝3，那么AC等于（）

A、3sinα B、3cosα C、 $\frac{3}{sin α}$ D、 $\frac{3}{cos α}$

查看试题解析
4. 点把 $A B$ 分割成 $A P$ 和 $P B$ 两段，如果 $A P$ 是 $P B$ 和 $A B$ 的比例中项，那么下列式子成立的是（　　）

A、 $\frac{P B}{A P} = \frac{\sqrt{5} + 1}{2}$ B、 $\frac{A P}{P B} = \frac{\sqrt{5} - 1}{2}$ C、 $\frac{P B}{A B} = \frac{\sqrt{5} - 1}{2}$ D、 $\frac{A P}{A B} = \frac{\sqrt{5} - 1}{2}$

查看试题解析
5. 如图，点 $D$ 、 $E$ 分别在 $△ A B C$ 的边 $A B$ 、 $A C$ 上，且 $D E$ 与 $B C$ 不平行．下列条件中，能判定 $△ A D E$ 与 $△ A C B$ 相似的是（　　）

A、 $\frac{A D}{A C} = \frac{A E}{A B}$ B、 $\frac{A D}{A E} = \frac{A B}{A C}$ C、 $\frac{D E}{B C} = \frac{A E}{A B}$ D、 $\frac{D E}{B C} = \frac{A D}{A C}$

查看试题解析
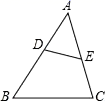6. 下列说法错误的是（）

A、设 $\vec{e}$ 为单位向量，那么 $| \vec{e} | = 1$ B、已知 $\vec{a}$ 、 $\vec{b}$ 、 $\vec{c}$ 都是非零向量，如果 $\vec{a} = 2 \vec{c}$ ， $\vec{b} = - 4 \vec{c}$ ，那么 $\vec{a} / / \vec{b}$ C、四边形 $A B C D$ 中，如果满足 $A B / / C D$ ， $| \vec{A D} | = | \vec{B C} |$ ，那么这个四边形一定是平行四边形 D、平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解

查看试题解析

二、填空题

7. 不等式 $2 x - 1 > 0$ 的解是．

查看试题解析
8. 方程 $\frac{1}{x - 1} = \frac{x^{2}}{x - 1}$ 的根是．

查看试题解析
9. 已知 $\frac{x}{y} = \frac{2}{5}$ ，那么 $\frac{x + y}{y}$ 的值是．

查看试题解析
10. $△ A B C ∽ △ A_{1} B_{1} C_{1}$ ，其中点 $A, B, C$ 分别与点 $A_{1}, B_{1}, C_{1}$ 对应，如果 $A B : A_{1} B_{1} = 2 : 3$ ， $A C = 6$ ，那么 $A_{1} C_{1} =$ ．

查看试题解析
11. 如图，在点 $A$ 处测得点 $B$ 处的仰角是．（用“ $∠ 1 ， ∠ 2 ， ∠ 3$ 或 $∠ 4$ ”表示）

查看试题解析
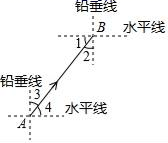12. 如图，当小明沿坡度i=1： $\sqrt{3}$ 的坡面由A到B行走了6米时，他实际上升的高度BC=米．

查看试题解析
13. 抛物线 $y = a x^{2} + (a - 1) (a \neq 0)$ 经过原点，那么该抛物线在对称轴左侧的部分是的.（填“上升”或“下降”）

查看试题解析
14. 如图4， $A D ∥ B C$ ， $A C$ 、 $B D$ 相交于点 $O$ ，且 $S_{△ A O D} ： S_{△ B O C} = 1 ： 4$ ．设 $\overset{⇀}{A D} = \overset{⇀}{a}$ ， $\overset{⇀}{D C} = \overset{⇀}{b}$ ，那么向量 $\overset{⇀}{A O} =$ ．（用向量 $\overset{⇀}{a}$ 、 $∵ x_{1} ， x_{2} \in R$ 表示）

查看试题解析
15. 在直角△ABC中，∠C＝90°，AC＝8，BC＝6，G是重心，那么G到斜边AB中点的距离是．

查看试题解析
16. 抛物线 $y = a x^{2} (a \neq 0)$ 沿某条直线平移一段距离，我们把平移后得到的新抛物线叫做原抛物线的“同簇抛物线”．如果把抛物线 $y = x^{2}$ 沿直线 $y = x$ 向上平移，平移距离为 $\sqrt{2}$ 时，那么它的“同簇抛物线”的表达式是．

查看试题解析
17. 如图，梯形 $A B C D$ 中， $A B ∥ C D$ ， $B E ∥ A D$ ，且 $B E$ 交 $C D$ 于点 $E$ ， $∠ A E B = ∠ C$ ．如果 $A B = 3$ ， $C D = 8$ ，那么 $A D$ 的长是．

查看试题解析
18. 如图，将矩形 $A B C D$ 沿对角线 $B D$ 所在直线翻折后，点 $A$ 与点 $E$ 重合，且 $E D$ 交 $B C$ 于点 $F$ ，连接 $A E$ ．如果 $tan ∠ D F C = \frac{2}{3}$ ，那么 $\frac{B D}{A E}$ 的值是．

查看试题解析

三、解答题

19. 计算： $\frac{2 {sin}^{2} 60 ° - cos 60 °}{{tan}^{2} 60 ° + 4 cos 45 °}$ ．

查看试题解析
20. 先化简，再求值： $(2 - \frac{x - 1}{x + 1}) \div (\frac{x^{2} + 6 x + 9}{x^{2} - 1})$ ，其中 $x = 2$ ．

查看试题解析
21. 已知：如图，反比例函数的图象经过点 $A$ 、 $P$ ，点 $A （ 6 ， \frac{4}{3} ）$ ，点 $P$ 的横坐标是2．抛物线 $y = {ax}^{2} + bx + c （ a \neq 0 ）$ 经过坐标原点，且与 $x$ 轴交于点 $B$ ，顶点为 $P$ ．
求：

(1)、反比例函数的解析式；

(2)、抛物线的表达式及 $B$ 点坐标．

查看试题解析
22. 如图，在某一路段，规定汽车限速行驶，交通警察在此限速路段的道路上设置了监测区，其中点C、D为监测点，已知点C、D、B在同一直线上，且AC⊥BC，CD＝400米，tan∠ADC＝2，∠ABC＝35°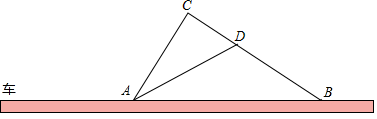

(1)、求道路AB段的长（结果精确到1米）

(2)、如果道路AB的限速为60千米/时，一辆汽车通过AB段的时间为90秒，请你判断该车是否是超速，并说明理由；参考数据：sin35°≈0.5736，cos35°≈0.8192，tan35°≈0.7002

查看试题解析
23. 已知：如图，在△ABC中，点D、E分别在边BC和AB上，且AD＝AC，EB＝ED，分别延长ED、AC交于点F．

(1)、求证：△ABD∽△FDC；

(2)、求证：AE²＝BE•EF．

查看试题解析
24. 在平面直角坐标系xOy中（如图），已知抛物线y＝ax²+bx+c（a≠0）的图象经过点B （4，0）、D （5，3），设它与x轴的另一个交点为A（点A在点B的左侧），且△ABD的面积是3．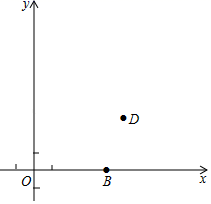

(1)、求该抛物线的表达式；

(2)、求∠ADB的正切值；

(3)、若抛物线与y轴交于点C，直线CD交x轴于点E，点P在射线AD上，当△APE与△ABD相似时，求点P的坐标．

查看试题解析
25. 已知：如图，在 $△ A B C$ 中， $A B = 6$ ， $A C = 9$ ， $tan ∠ A B C = 2 \sqrt{2}$ ．过点 $B$ 作 $B M ∥ A C$ ，动点 $P$ 在射线 $B M$ 上（点 $P$ 不与 $B$ 重合），联结 $P A$ 并延长到点 $Q$ ，使 $∠ A Q C = ∠ A B P$ ．

(1)、求 $△ A B C$ 的面积；

(2)、设 $B P = x$ ， $A Q = y$ ，求 $y$ 关于 $x$ 的函数解析式，并写出 $x$ 的取值范围；

(3)、连接 $P C$ ，如果 $△ P Q C$ 是直角三角形，求 $B P$ 的长．

查看试题解析